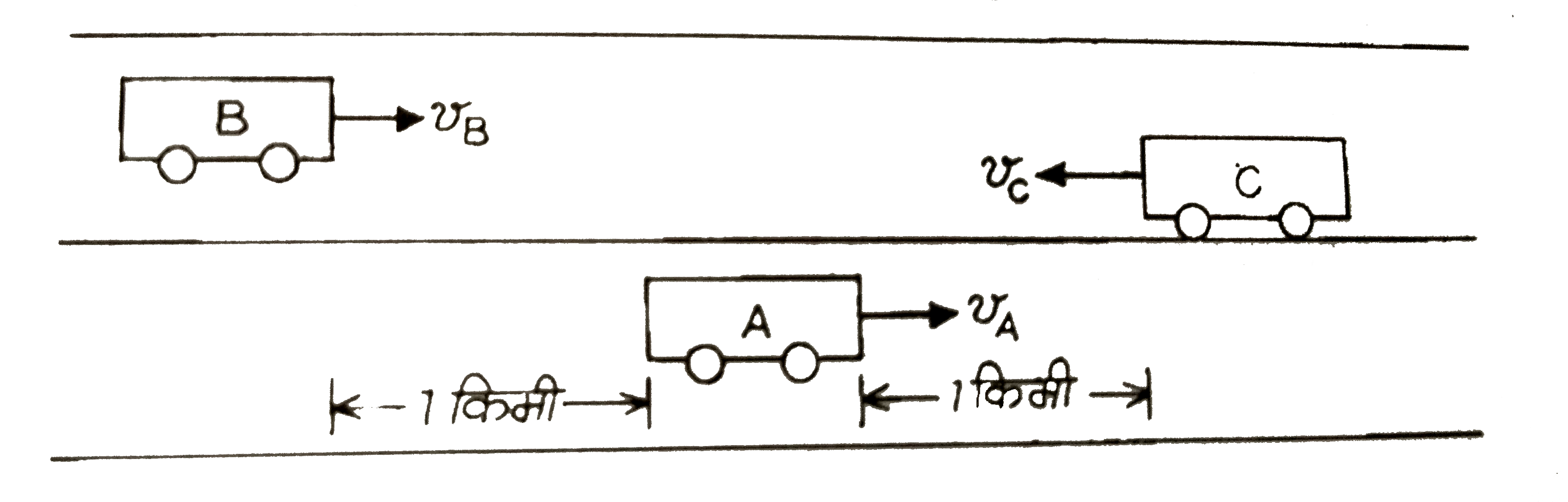
दो -लेन वाली किसी सड़क पर कार A36kmh−1 की चाल से चल रही है । एक-दूसरे की विपरीत दिशाओं में चलती दो कारें B व C जिनमें से प्रत्येक की चाल 54kmh−1 है, कार A तक पहुँचना चाहती हैं। किसी क्षण जब दूरी AB दूरी AC के बराबर है तथा दोनों 1km है , कार B का चालक यह निर्णय करता है कि कार C के कार A तक पहुँचने के पहले ही वह कार A से आगे निकल जाए । किसी दुर्घटना से बचने के लिए कार B का कितना न्यूनतम त्वरण जरूरी है ?
तीनो कारो की गति चित्र में प्रदर्शित है । माना कारों A,B व C के वेग क्रमश: vA,vB व vC है । माना कारे A व B धनात्मक X- दिशा में गतिमान है जबकि C ऋणात्मक X- दिशा में चल रही है । प्रश्नानुसार ,
vA=36 किमी/घण्टा =36×518 मी/से = 10 मी/से
vB=54 किमी/घण्टा =54×518 मी/से = 15 मी/से
vC=−54 किमी/घण्टा =−15 मी/से
कार A का B कार के सापेक्ष वेग
vBA=vB−vA=15−10=5 मी/से
कार C का कार A के सापेक्ष वेग
vCA=vC−vA=−15−10=−25 मी/से
ऋणात्मक चिन्ह यह प्रकट करता है की vCA, ऋणात्मक X-दिशा में है । यदि दूरी BA=(=1किमी=1000मीटर) तय करने में लिया गया समय t , हो तो
t=दूरीवेग=1000मीटर25मी/से−1=40 सेकण्ड ।
यदि कार B कार A को कार C की अपेक्षा पहले ओवरटेक करे, तो कार B को इस प्रकार त्वरित करना होगा की कार A द्वारा तय की गई दूरी AB=1000 मीटर, 5 मी/से की चाल से 40 सेकण्ड से थोड़ा कम समय में ही तय हो जाय, अतः
सूत्र s=ut+12at2 से,
1000=5×40+12a×(40)2
अथवा 800a=1000−200
अतः त्वरण a=800800=1मी से−2 ।
Topper's Solved these Questions
- ऋजु रेखीय पथ पर गति BOOK - NOOTAN HINDICHAPTER - ऋजु रेखीय पथ पर गति EXERCISE - अतिरिक्त प्रश्न
6 Videos
- ऋजु रेखीय पथ पर गति BOOK - NOOTAN HINDICHAPTER - ऋजु रेखीय पथ पर गति EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न) (एकल उत्तर प्रकार)
18 Videos
- ऊष्मा स्थानांतरण BOOK - NOOTAN HINDICHAPTER - ऊष्मा स्थानांतरण EXERCISE - अतिरिक्त प्रश्न
2 Videos
- कार्य, शक्ति एवं ऊर्जा BOOK - NOOTAN HINDICHAPTER - कार्य, शक्ति एवं ऊर्जा EXERCISE - अतिरिक्त प्रश्न
7 Videos
Similar Questions
कोई तीन पहिये वाला स्कूटर अपनी विरामावस्था से गति प्रारम्भ करता हैं फिर 10s तक किसी सीधी सड़क पर 1ms−2 के एकसमान त्वरण से चलता है। इसके बाद वह एकसमान वेग से चलता है । स्कूटर द्वारा nवें सेकण्ड (n=1,2,3........) में तय की गई दूरी को n के सापेक्ष आलेखित कीजिए । आप क्या आशा करते हैं की त्वरित गति के दौरान यह ग्राफ कोई सरल रेखा या कोई परवलय होगा ?
View Solutionदिये गये सभी ग्राफ एक ही गति को दर्शाते हैं । कोई एक ग्राफ उस गति को गलत तरीके से दर्शाता है । वह ग्राफ है :
View SolutionCO2 के P -T प्रावस्था आरेख पर आधारित निम्नलिखित प्रश्नो के उत्तर दीजिए:
(a ) किस ताप व दाब पर CO2 की ठोस,द्रव तथा वाष्प प्रावस्थाएँ साम्य में सहवर्ती हो सकती है?
(b ) CO2 के गलनांक तथा क्वथनांक पर दाब में कमी का क्या प्रभाव पड़ता है?
(c ) CO2 के लिए क्रांतिक ताप तथा दाब क्या है?इसका क्या महत्व है?
(d ) (i ) −70∘C ताप व 1 atm दाब (ii ) −60∘C ताप व 10 atm दाब ,(iii ) 15∘C ताप व 56 atm दाब पर CO2 ठोस,द्रव अथवा गैस में किस अवस्था में होती है?
View Solution0.012kg द्रव्यमान की कोई गोली 70ms−1 की क्षैतिज चाल से चलते हुए 0.4 kg द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरन्त ही विरामावस्था में आ जाती है । गुटके को छत से पतली तारों द्वारा लटकाया गया है। परिकलन कीजिए कि गुटका किस ऊँचाई तक ऊपर उठता है? गुटके में पैदा हुई ऊष्मा की मात्रा का भी अनुमान लगाइए ।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View SolutionIf a boat goes upstream at a speed fo 18 km /hr and comes back the same distance at 30 km/ hr.What is the average speed (in km /hr)for the total journey?
कोई नाव धारा के विपरीत दिशा में 10 किलोमीटर /घंटा की चाल से चलती है और समान दूरी पर 30 किलोमीटर/घंटा की चाल से वापस आती है। कुल यात्रा के लिए औसत चाल किलोमीटर/ घंटा में) क्या है?
View Solutionरमन बस से 5Km 52m, कार से 2Km 265 m तथा साइकिल से 1Km 30m की दूरी तय करता है तब कुल दूरी होगी -
View SolutionThe distance between two stations A and B is 800 km. A train X starts from point A and moves towards point B at a speed of 40 km/h and another train Y starts from point B and moves towards A at 60 km/h. How far from A will they cross each other?
दो स्टेशनों A और B के बीच की दूरी 800 किमी है | एक ट्रेन X बिंदु A से चलती है और B की तरफ 40 किमी/घंटा की चाल से जाती है तथा दूसरी ट्रेन Y बिंदु B से A की ओर 60 किमी/घंटा की चाल से चलना शुरू करती है | A से कितनी दूरी पर वे एक-दूसरे को पार करेंगी ?
View SolutionAmit travelled from A to B at an average speed of 80 km/h. He travelled the first 75% of the distance in two-third of the time and the rest at a constant speed of x km/h. The value of x is:
अमित ने A से B तक 80 किमी/घंटा की औसत चाल से यात्रा की | उसने पहली 75% दूरी दो-तिहाई समय में तथा शेष दूरी x किमी/घंटा की चाल से तय की | x का मान क्या है ?
View SolutionA person covers 40% of a distance with a speed of 60 km/h and the remaining with a speed of 40 km/h. What is his average speed for the whole journey in km/h?
एक व्यक्ति किसी दूरी का 40% हिस्सा 60 किमी/घंटा की चाल से तथा शेष दूरी 40 किमी/घंटा की चाल से तय करता है | पूरी यात्रा में उसकी औसत चाल ( किमी/घंटा में ) ज्ञात करें |
View SolutionA person covers 40% of the distance from A to B at 8 km/h, 40% of the remaining distance at 9 km/h and the rest at 12 km/h. His average speed (in km/h) for the journey is :
एक व्यक्ति A से B तक की 40% दूरी 8 किमी/घंटा की चाल से, शेष दूरी का 40%, 9 किमी/घंटा की चाल से तथा शेष टूरी 12 किमी/घंटा की चाल से तय करता है | इस यात्रा में उसकी औसत चाल ( किमी/घंटा में ) कितनी रही है ?
View SolutionA car covers 25 km at a uniform speed. If the speed had been 8 km/h more, it would have taken 10 hours less for the same journey. What is the speed of the car (in km/h)?
एक कार 25 किमी की दूरी एक समान चाल से तय करती है | यदि चाल 8 किमी/घंटा अधिक होती, तो इसे इस यात्रा में 10 घंटे कम लगते | कार की चाल ( किमी/घंटा में)कितनी है?
View SolutionA car can cover a distance of 18 km in 24 minutes. The speed of a bus is twice that of a car. In how many minutes can the bus cover a distance of 135 km?
एक कार 24 मिनट में 18 km की दूरी तय कर सकती है | किसी बस की गति कार की दुगुनी है | बस 135km की दूरी कितने मिनट में तय कर सकती है ?
View SolutionA man goes to a place on car at speed of 160 km/h and comes back at lower speed. If the average speed is 64 km/h in total, them the return speed (in km/h) is:
एक व्यक्ति कार से किसी स्थान को 160 किमी/घंटा की चाल से जाता है तथा कम चाल से वापस आता है | यदि कुल मिलाकर औसत चाल 64 किमी/घंटा है, तो वापसी की चाल (किमी/घंटा में ) है
View Solution
