किसी गेंद को 90 m की ऊँचाई से फर्श पर गिराया जाता है । फर्श के साथ प्रत्येक टक्कर के गेंद की चाल 1/10 कम हों जाती है । इसकी गति का t=0 से 12 sके बीच चाल-समय ग्राफ खींचिए ।
माना गेंद t समय पश्चात फर्श पर टकराती है , तब समीकरण h=ut+12gt2 , u=0,h=90मीटर एवं g=9.8मी/से2 रखने पर ,
90=(0×t)+12×9.8×t2
अथवा t2=2×909.8=90049
अथवा t=307=4.28 सेकण्ड ।
अब माना गेंद मुक्त रूप से गिरते हुए फर्श से v वेग से टकराती है । तब,
v=u+gt=0+(9.8×307)=42मी/से
चूँकि फर्श पर टकराने के बाद गेंद अपने वेग का दसवाँ हिस्सा खो देती है । अतः गेंद का टकराने के बाद नया वेग,
v'=910×42=37.8 मी/से
अब माना गेंद का वेग t' सेकण्ड बाद शून्य हो जाता है, तब समीकरण v=u−gt में v=0,u=v'=37.8मी/से, t=t' तथा g=9.8मी/से2 रखने पर,
0=37.8−9.8t'
अथवा t'=37.89.8=3.86 सेकण्ड
अब एक बार पुनः गिरने एवं फर्श से टकराने के ठीक पूर्व गेंद का वेग 37.8 मी/से होगा और इस दौरान वह कुल 3.86 सेकण्ड का समय लेगी । अतः
t''=3.86 सेकण्ड
फलतः इस क्षण तक लिया गया कुल समय, t+t'+t' सेकण्ड
=4.28+3.86+3.86=12सेकण्ड
तथा दूसरी टक्कर के बाद गेंद का वेग,
v''=910×37.8=34.0
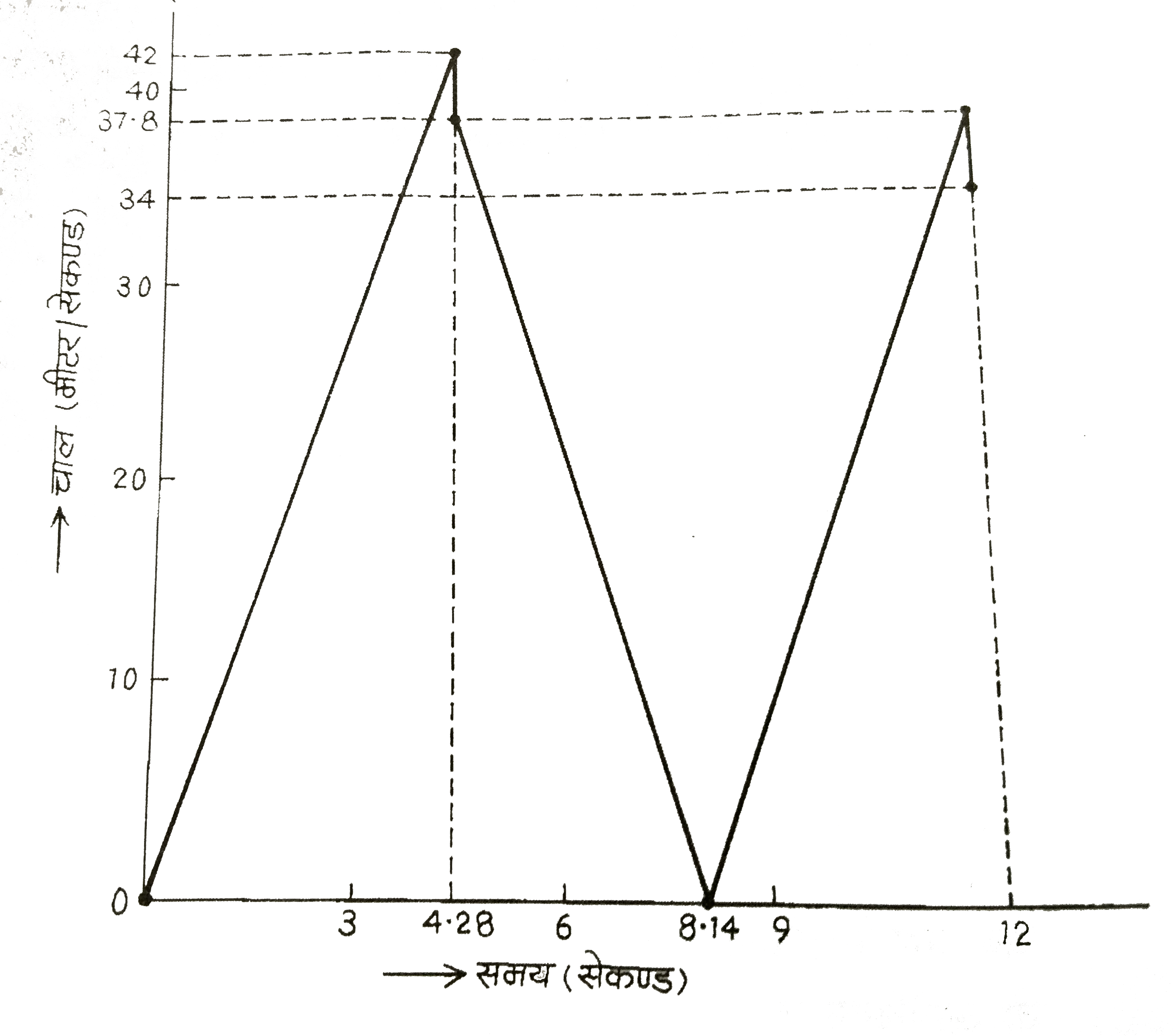
अतः इस प्रक्रिया के विभिन्न चरणों में समय एवं चाल के आँकड़े निम्नलिखित होंगे -
समय चाल004.28सेकण्ड42मी/से−−→37.88.14सेकण्ड012.0सेकण्ड37.8मी/से−−→34
तथा इस गति का चाल-समय ग्राफ निम्नांकित है :
Topper's Solved these Questions
- ऋजु रेखीय पथ पर गति BOOK - NOOTAN HINDICHAPTER - ऋजु रेखीय पथ पर गति EXERCISE - अतिरिक्त प्रश्न
6 Videos
- ऋजु रेखीय पथ पर गति BOOK - NOOTAN HINDICHAPTER - ऋजु रेखीय पथ पर गति EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न) (एकल उत्तर प्रकार)
18 Videos
- ऊष्मा स्थानांतरण BOOK - NOOTAN HINDICHAPTER - ऊष्मा स्थानांतरण EXERCISE - अतिरिक्त प्रश्न
2 Videos
- कार्य, शक्ति एवं ऊर्जा BOOK - NOOTAN HINDICHAPTER - कार्य, शक्ति एवं ऊर्जा EXERCISE - अतिरिक्त प्रश्न
7 Videos
Similar Questions
कोई तीन पहिये वाला स्कूटर अपनी विरामावस्था से गति प्रारम्भ करता हैं फिर 10s तक किसी सीधी सड़क पर 1ms−2 के एकसमान त्वरण से चलता है। इसके बाद वह एकसमान वेग से चलता है । स्कूटर द्वारा nवें सेकण्ड (n=1,2,3........) में तय की गई दूरी को n के सापेक्ष आलेखित कीजिए । आप क्या आशा करते हैं की त्वरित गति के दौरान यह ग्राफ कोई सरल रेखा या कोई परवलय होगा ?
View Solutionदिये गये सभी ग्राफ एक ही गति को दर्शाते हैं । कोई एक ग्राफ उस गति को गलत तरीके से दर्शाता है । वह ग्राफ है :
View SolutionCO2 के P -T प्रावस्था आरेख पर आधारित निम्नलिखित प्रश्नो के उत्तर दीजिए:
(a ) किस ताप व दाब पर CO2 की ठोस,द्रव तथा वाष्प प्रावस्थाएँ साम्य में सहवर्ती हो सकती है?
(b ) CO2 के गलनांक तथा क्वथनांक पर दाब में कमी का क्या प्रभाव पड़ता है?
(c ) CO2 के लिए क्रांतिक ताप तथा दाब क्या है?इसका क्या महत्व है?
(d ) (i ) −70∘C ताप व 1 atm दाब (ii ) −60∘C ताप व 10 atm दाब ,(iii ) 15∘C ताप व 56 atm दाब पर CO2 ठोस,द्रव अथवा गैस में किस अवस्था में होती है?
View Solution0.012kg द्रव्यमान की कोई गोली 70ms−1 की क्षैतिज चाल से चलते हुए 0.4 kg द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरन्त ही विरामावस्था में आ जाती है । गुटके को छत से पतली तारों द्वारा लटकाया गया है। परिकलन कीजिए कि गुटका किस ऊँचाई तक ऊपर उठता है? गुटके में पैदा हुई ऊष्मा की मात्रा का भी अनुमान लगाइए ।
View Solutionलोहे की 0.10 किग्रा की एक गेंद 10 मीटर की ऊँचाई से गिराई जाती है तथा पृथ्वी से टकराकर पुनः 1 मीटर की ऊँचाई तक उछल जाती है मान लीजिए कि गेंद कि यान्त्रिक ऊर्जा का क्षय हुआ अंश पूर्णतः गेंद में ही रह जाता है । गेंद है । गेंद के पदार्थ की विशिष्ट ऊष्मा 0.12 कैलोरी /(ग्राम -°C) है । (i) क्या गेंद को ऊष्मा दी गई ?(ii) क्या गेंद पर कार्य किया गया ? यदि हाँ तो कितना ? (iii) गेंद की आन्तरिक ऊर्जा में क्या परिवर्तन हुआ ? (iv) टकराने पर गेंद के ताप में कितनी वृद्धि हुई ?(g=10 न्यूटन /किग्रा , 4.2J = 1 कैलोरी )
View Solutionदो पासो को एक साथ चार बार फेका जाता है दोनों पासो पर प्राप्त अंको का योग 7 कम से कम दो बार आने की प्रायिकता ज्ञात कीजिए
View Solutionअतिपरवलय के किसी बिंदु से इसकी अनन्तस्पर्शियों पर डाले गए लंबों का गुणनफल है
View Solutionग्राफ की सहायता से गति के समीकरणों को व्युत्पन्न करना
View Solutionएक थैले में 3 सफेद और 5 काली गेंदें हैं। थैले के अंदर से बिना देखे एक गेंद निकाली जाती है।
(a) एक सफेद गेंद प्राप्त करने की प्रायिकता क्या है?
(b) एक काली गेंद प्राप्त करने की प्रायिकता क्या है?
View Solutionएक वस्तु पूर्व दिशा की ओर 30 मी/से के वेग से जा रही है। 10 सेकण्ड के बाद यह वस्तु 40 मी/से के वेग से उत्तर की ओर गति करती है। वस्तु का औसत त्वरण है-
View SolutionA man goes to a place on car at speed of 160 km/h and comes back at lower speed. If the average speed is 64 km/h in total, them the return speed (in km/h) is:
एक व्यक्ति कार से किसी स्थान को 160 किमी/घंटा की चाल से जाता है तथा कम चाल से वापस आता है | यदि कुल मिलाकर औसत चाल 64 किमी/घंटा है, तो वापसी की चाल (किमी/घंटा में ) है
View Solution4 किमी /घण्टा की चाल से अपने घर से चलकर अमित अपने स्कूल में निर्धारित समय से 10 मिनट पहले पहुंच जाता है। यह वि 3 किमी/घण्टा की चाल से चले, तो निश्चित समय से 10 मिनट देर से पहुंचता है। उसके घर तथा स्कूल के बीच की दूरी है
View SolutionGautam goes to office at a speed of 12 kmph and returns home at 10 kmph. His average speed is गौतम 12 किमी०/घंटा की चाल से कार्यालय जाता है और 10 किमी०/घंटा की चाल से वापस आता है। उसकी औसत चाल बताइए?
View SolutionRevision|किसी ऊँचाई से, यदि वस्तु ऊर्ध्वाधर नीचे की ओर कुछ प्रारम्भिक वेग से फेंकी जाये |गति के समीकरण |किसी ऊँचाई से यदि किसी वस्तु को गिराया जाये (प्रारम्भिक वेग शून्य)|किसी ऊँचाई से, यदि वस्तु ऊर्ध्वाधर ऊपर की ओर कुछ प्रारम्भिक वेग से फेंकी जाये |वस्तु की वायु की उपस्थिति मे गति |प्रश्न |OMR|Summary
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solutionजब एल्कोहॉल की वाष्प को गर्म तांबे के ऊपर से गुजारा जाता है, तो एल्कोहॉल शीघ्रता से एल्कीन में रूपांतरित हो जाती है, एल्कोहॉल है:
View Solution
