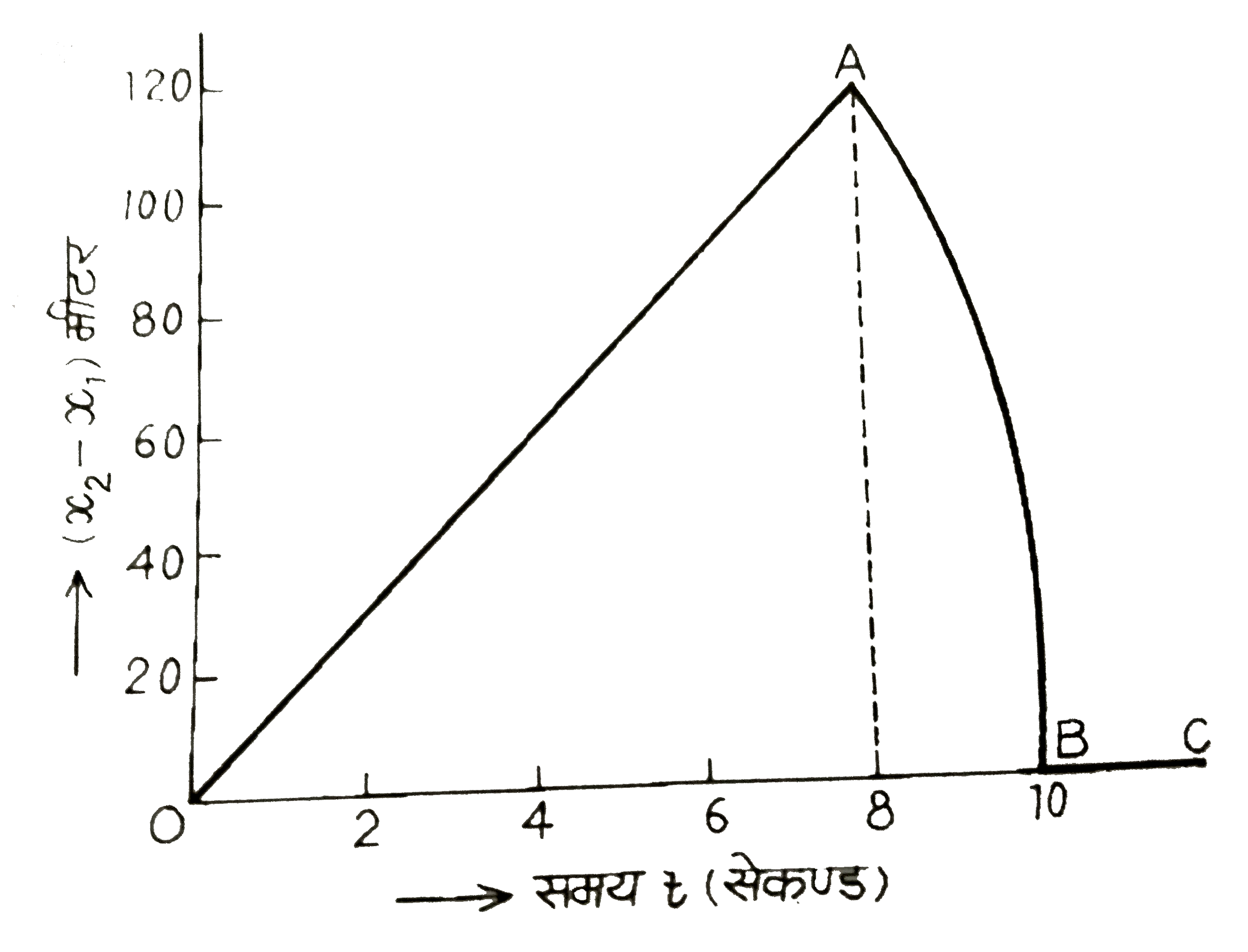
किसी 200 m ऊँची खड़ी चटट्न के किनारे से दो पत्थरों को एक साथ ऊपर की और 15ms−1 तथा 30ms−1 की प्रारम्भिक चाल से फेंका जाता है । इसका सत्यापन कीजिए कि नीचे दिखाया गया ग्राफ (चित्र) पहले पत्थर के सापेक्ष दूसरे पत्थर की आपेक्षिक स्थिति का समय के साथ परिवर्तन को प्रदर्शित करता है । वायु के प्रतिरोध को नगण्य मानिए और यह मानिए कि जमीन से टकराने के बाद पत्थर ऊपर की और उछलते नहीं । मान लीजिए g=10ms−2 । ग्राफ के रेखीय व वक्रीय भागों के लिए समीकरण लिखिए ।
पहले पत्थर के लिए : माना पृथ्वी का तल पत्थर की स्थिति की माप के लिए मूलबिंदु है । प्रारम्भिक स्थिति x0=200 मीटर
प्रारम्भिक वेग, u1=15 मीसे−1,a=−g=−10मीसे−2
सूत x1=x0+u1t+12at2 से
x1=2000+15t−12×10t2=200+15t−5t2........(i)
जब पहला पत्थर पृथ्वी से टकराता है , तो x1=0
∴200+15t−5t2=0
अथवा 5t2−15t−200=0 अथवा t2=−3t−40=0
इससे t=−5 सेकण्ड या 8 सेकण्ड
चूँकि t = - 5 सेकण्ड अनुमेय नहीं है । ∴t=8 सेकण्ड ।
दूसरे पत्थर के लिए : प्रारम्भिक वेग u2=30मीसे−1 अतः सूत्र
x2=x0+u2t+12at2
x2=200+30t−12×10t2.......(ii)
जब दूसरा पत्थर पृथ्वी से टकराता है , तो x2=0
∴200+30t−5t2=0 अथवा t2−6t−40=0
इससे t=−4 सेकण्ड या 10 सेकण्ड
चूँकि t=−4 सेकण्ड अनुमेय नहीं है । ∴t=10 सेकण्ड
दूसरे पत्थर की पहले पत्थर के सापेक्ष स्थिति,
x2−x1=15t.........(iii)
स्पष्टतः x2−x1 तथा t के बीच ग्राफ सरल रेखा है
यह समीकरण केवल 8 सेकण्ड तक के लिए उपयुक्त है । 8 सेकण्ड पश्चात केवल दूसरा पत्थर गति में है , अतः इसका गति समीकरण (ii) से प्रदर्शित होगा । अर्थात
x2=200+3t−5t2..........(iv)
यह एक द्विघातीय समीकरण जिसका x-t ग्राफ एक वक्र होगा जो की ग्राफ के भाग AB से प्रदर्शित है , यह वक्र से सेकण्ड के बीच समीकरण (iv) को सन्तुष्ट करता है ।
Topper's Solved these Questions
- ऋजु रेखीय पथ पर गति BOOK - NOOTAN HINDICHAPTER - ऋजु रेखीय पथ पर गति EXERCISE - एनo सीo ईo आरo टीo प्रश्न
22 Videos
- ऊष्मा स्थानांतरण BOOK - NOOTAN HINDICHAPTER - ऊष्मा स्थानांतरण EXERCISE - अतिरिक्त प्रश्न
2 Videos
- कार्य, शक्ति एवं ऊर्जा BOOK - NOOTAN HINDICHAPTER - कार्य, शक्ति एवं ऊर्जा EXERCISE - अतिरिक्त प्रश्न
7 Videos
Similar Questions
नीचे दिए गए गति के कौन-से उदाहरणों में वस्तु को लगभग बिन्दु वस्तु माना जा सकता है :
(a) दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी ।
(b) किसी वृत्तीय पथ पर साइकल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बन्दर ।
(c ) जमीन से टकराकर तेजी से मुड़ने वाली क्रिकेट कि कोई फिरकती गेंद ।
(d) किसी मेज के किनारे से फिसलकर गिरा कोई बीकर ।
View SolutionCO2 के P -T प्रावस्था आरेख पर आधारित निम्नलिखित प्रश्नो के उत्तर दीजिए:
(a ) किस ताप व दाब पर CO2 की ठोस,द्रव तथा वाष्प प्रावस्थाएँ साम्य में सहवर्ती हो सकती है?
(b ) CO2 के गलनांक तथा क्वथनांक पर दाब में कमी का क्या प्रभाव पड़ता है?
(c ) CO2 के लिए क्रांतिक ताप तथा दाब क्या है?इसका क्या महत्व है?
(d ) (i ) −70∘C ताप व 1 atm दाब (ii ) −60∘C ताप व 10 atm दाब ,(iii ) 15∘C ताप व 56 atm दाब पर CO2 ठोस,द्रव अथवा गैस में किस अवस्था में होती है?
View Solution0.012kg द्रव्यमान की कोई गोली 70ms−1 की क्षैतिज चाल से चलते हुए 0.4 kg द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरन्त ही विरामावस्था में आ जाती है । गुटके को छत से पतली तारों द्वारा लटकाया गया है। परिकलन कीजिए कि गुटका किस ऊँचाई तक ऊपर उठता है? गुटके में पैदा हुई ऊष्मा की मात्रा का भी अनुमान लगाइए ।
View Solutionग्राफ की सहायता से गति के समीकरणों को व्युत्पन्न करना
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solution2 N HCI के 25 ml, 4 N HNO_3 के 50 ml और 2 M H_2SO_4 के v ml को एक साथ मिलाया जाता है और कुल आयतन को 1 L तक तैयार किया जाता है, तनुकरण के बाद इस अम्ल मिश्रण का 50 ml, 1 N Na_2CO_3 के 25 ml के साथ पूर्णतया अभिक्रिया करता है। v का मान है
View Solutionजब दो तत्वों A और D के दो यौगिकों ACl_(3) और DCl_(3) को एक साथ मिश्रित किया जाता है, तो एक यौगिक ADCl_(6) का निर्माण होता है। संरचनात्मक विश्लेषण से पता चला कि ADCl_(6) एक आयनिक यौगिक है। दिया गया है कि DCl_(3) त्रिकोणीय समतल है और ACl_(3) त्रिकोणीय पिरामिडीय है, ऋणायन DCl_(4)^(-) की आकृति ज्ञात कीजिए।
View Solutionसंगलित अशुद्ध धातु को लकड़ी के हरे रंग के लट्टे के साथ हिलाकर फफोलेदार तांबा को परिष्कृत किया जाता है, क्योंकि इस प्रकार की लकड़ी, हाइड्रोकार्बन गैसों (जैसे CH_4 ) को मुक्त करती है। इस प्रक्रम X को ________ कहा जाता है और इसका उपयोग धातु में प्रारंभ में उपस्थित Y की अशुद्धियों के शुद्धिकरण के लिए किया जाता है। Y _______ है।
View Solutionग्लूकोज के ताजा तैयार विलयन से समय के साथ प्रकाशिक घूर्णन में परिवर्तन को निम्न में जाना जाता है -
View Solution10N−H2SO4 के 50 ml, 12N-HCL के 25 ml, और 5N–HNO3 के 40 ml को एक साथ मिलाया जाता है और जल मिलाकर मिश्रण का आयतन 1000 ml किया जाता है। परिणामी विलयन की नॉर्मलता होगी
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solutionऐलुमीनियम क्लोराइड और क्यूप्रस क्लोराइड के उत्प्रेरक मिश्रण की उपस्थिति में ………. और ……….. की वाष्प को बेन्जीन विलयन में प्रवाहित करके बेन्जीन से बेन्जेल्डिहाइड को निर्मित किया जा सकता है। अभिक्रिया को ……….. के नाम से जाना जाता है ।
View Solution1 M NaOH विलयन के 2.5 लीटर को अन्य 0.5 M NaOH विलयन के 3 लीटर के साथ मिलाया जाता है। परिणामी विलयन की मोलरता है -
View Solutionनिम्नलिखित में से कौनसा आरेख एक प्रबल विद्युत अपघट्य के लिए तनुकरण के साथ तुल्यांकी चालकत्व (A) की सही परिवर्तनशीलता को प्रदर्शित करता है?
View Solutionबेन्जैल्डिहाइड बनाने के लिए AlCl3 की उपस्थिति में बेन्जीन के साथ CO+HCI की अभिक्रिया को क्या कहा जाता है?
View SolutionNaOH की उपस्थिति में, फीनॉल के साथ बेंजॉयल क्लोराइड की अभिक्रिया को कहा जाता है:
View Solution
