एकविमीय गति में किसी कण का वेग-समय ग्राफ चित्र में दिखाया गया है :
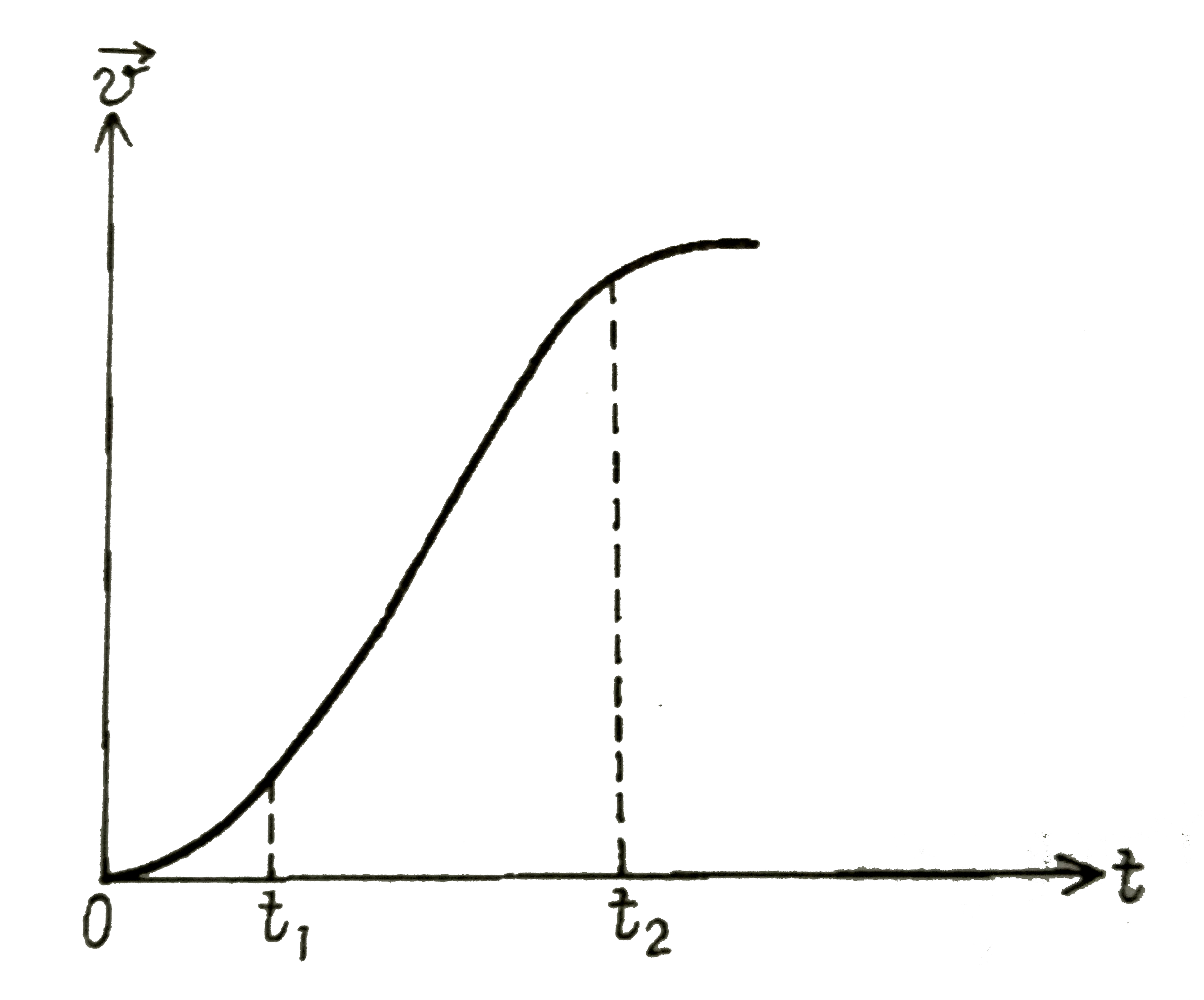
नीचे दिए सूत्रों में t1 से t2 तक के समय-अन्तराल की अवधि में कण की गति का वर्णन करने के लिए कौन -से सूत्र सही है ?
(a) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(b) v(t2)=v(t1)+a(t2−t1)
(c) vaverage=[x(t2)−x(t1)]/(t2−t1)
(d) aaverage=[v(t2)−v(t1)]/(t2−t1)
(e ) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(f) x(t2)−x(t1)=t- अक्ष तथा दिखाई गई बिन्दुकित रेखा के बीच दर्शाए गए वक्र के अन्तर्गत आने वाला क्षेत्रफल।
(a) यह असत्य है, क्योकि समय-अन्तरालो t1 व t2 में त्वरण a नियत नहीं है । (वेग - समय ग्राफ की ढाल जो की त्वरण होती है सभी बिन्दुओं पर समान नहीं है ) ।
(b) यह भी असत्य है । कारण वही है जो अनुभाग (a) के लिए लागू होते है ।
(c ) तथा (d) दोनों सत्य है, (परिभाषा के अनुसार)
(e ) यह असत्य है, क्योकि व्यंजक में औसत त्वरण का प्रयोग नहीं किया जाता है ।
(f) यह सत्य है क्योकि ग्राफ तथा अक्ष के बीच घिरा क्षेत्रफल सभी प्रकार की सरल रेखीय गतियों के लिए कण के विस्थापन को प्रकट करता है ।
Topper's Solved these Questions
- ऋजु रेखीय पथ पर गति BOOK - NOOTAN HINDICHAPTER - ऋजु रेखीय पथ पर गति EXERCISE - एनo सीo ईo आरo टीo प्रश्न
22 Videos
- ऊष्मा स्थानांतरण BOOK - NOOTAN HINDICHAPTER - ऊष्मा स्थानांतरण EXERCISE - अतिरिक्त प्रश्न
2 Videos
- कार्य, शक्ति एवं ऊर्जा BOOK - NOOTAN HINDICHAPTER - कार्य, शक्ति एवं ऊर्जा EXERCISE - अतिरिक्त प्रश्न
7 Videos
Similar Questions
नीचे दिए गए गति के कौन-से उदाहरणों में वस्तु को लगभग बिन्दु वस्तु माना जा सकता है :
(a) दो स्टेशनों के बीच बिना किसी झटके के चल रही कोई रेलगाड़ी ।
(b) किसी वृत्तीय पथ पर साइकल चला रहे किसी व्यक्ति के ऊपर बैठा कोई बन्दर ।
(c ) जमीन से टकराकर तेजी से मुड़ने वाली क्रिकेट कि कोई फिरकती गेंद ।
(d) किसी मेज के किनारे से फिसलकर गिरा कोई बीकर ।
View SolutionCO2 के P -T प्रावस्था आरेख पर आधारित निम्नलिखित प्रश्नो के उत्तर दीजिए:
(a ) किस ताप व दाब पर CO2 की ठोस,द्रव तथा वाष्प प्रावस्थाएँ साम्य में सहवर्ती हो सकती है?
(b ) CO2 के गलनांक तथा क्वथनांक पर दाब में कमी का क्या प्रभाव पड़ता है?
(c ) CO2 के लिए क्रांतिक ताप तथा दाब क्या है?इसका क्या महत्व है?
(d ) (i ) −70∘C ताप व 1 atm दाब (ii ) −60∘C ताप व 10 atm दाब ,(iii ) 15∘C ताप व 56 atm दाब पर CO2 ठोस,द्रव अथवा गैस में किस अवस्था में होती है?
View Solution0.012kg द्रव्यमान की कोई गोली 70ms−1 की क्षैतिज चाल से चलते हुए 0.4 kg द्रव्यमान के लकड़ी के गुटके से टकराकर गुटके के सापेक्ष तुरन्त ही विरामावस्था में आ जाती है । गुटके को छत से पतली तारों द्वारा लटकाया गया है। परिकलन कीजिए कि गुटका किस ऊँचाई तक ऊपर उठता है? गुटके में पैदा हुई ऊष्मा की मात्रा का भी अनुमान लगाइए ।
View SolutionIf the normals at points t1andt2 meet on the parabola, then t1t2=1 (b) t2=−t1−2t1 t1t2=2 (d) none of these
View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in Fig.:

(a) Which of the following formulae are correct for describing the motion of the particle over the time-interval t1 to t2:
(a) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(b) v(t2)=v(t1)+a(t2−t1)
(c) vaverage=(x(t2)−x(t1))/(t2−t1)
(d) aaverage=(v(t2)−v(t1))/(t2−t1)
(e) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(f) x(t2)−x(t1) = area under the v−t curve bounded by the t-axis and the dotted line shown.
View SolutionFor any arbitrary motion in space, which of the following relations are true?
(a) vaverage=(1/2)(v(t1)+v(t2))
(b) vaverage=[r(t2)−r(t1]/(t2−t1)
(c) v(t)=v(0)+at
(d) aaverage=[v(t2)−v(t1)]/(t2−t1)
The average stands for average of the quantity over time interval t1 to t2
View Solution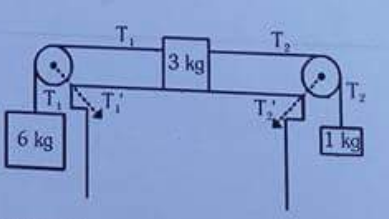
Calculate a, T1,T2,T1'&T2'.
View Solutionएकविमीय गति में किसी कण का वेग-समय ग्राफ चित्र 3.29 में दिखाया गया है :

नीचे दिए सूत्रों में t1 से t2 तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-सा सूत्र सही है :
(i) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(ii) v(t2)=v(t1)+a(t2−t1)
(iii) vaverage=[x(t2)−x(t1)]/(t2−t1)
(iv) aaverage=[v(t2)−v(t1)]/(t2−t1)
(v) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(vi) x(t2)−x(t1)=t-अक्ष तथा दिखाई गई बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल |
View Solutionदर्शाइए कि परवलय y2=4ax पर बिंदुओं t1,t2 और t3 से बने त्रिभुज के क्षेत्रफल का परिमाण a2(t1−t2)(t2−t3)(t3−t1) है।
View Solutionएकविमीय गति में किसी कण का वेग-समय ग्राफ चित्र में दिखाया गया है -
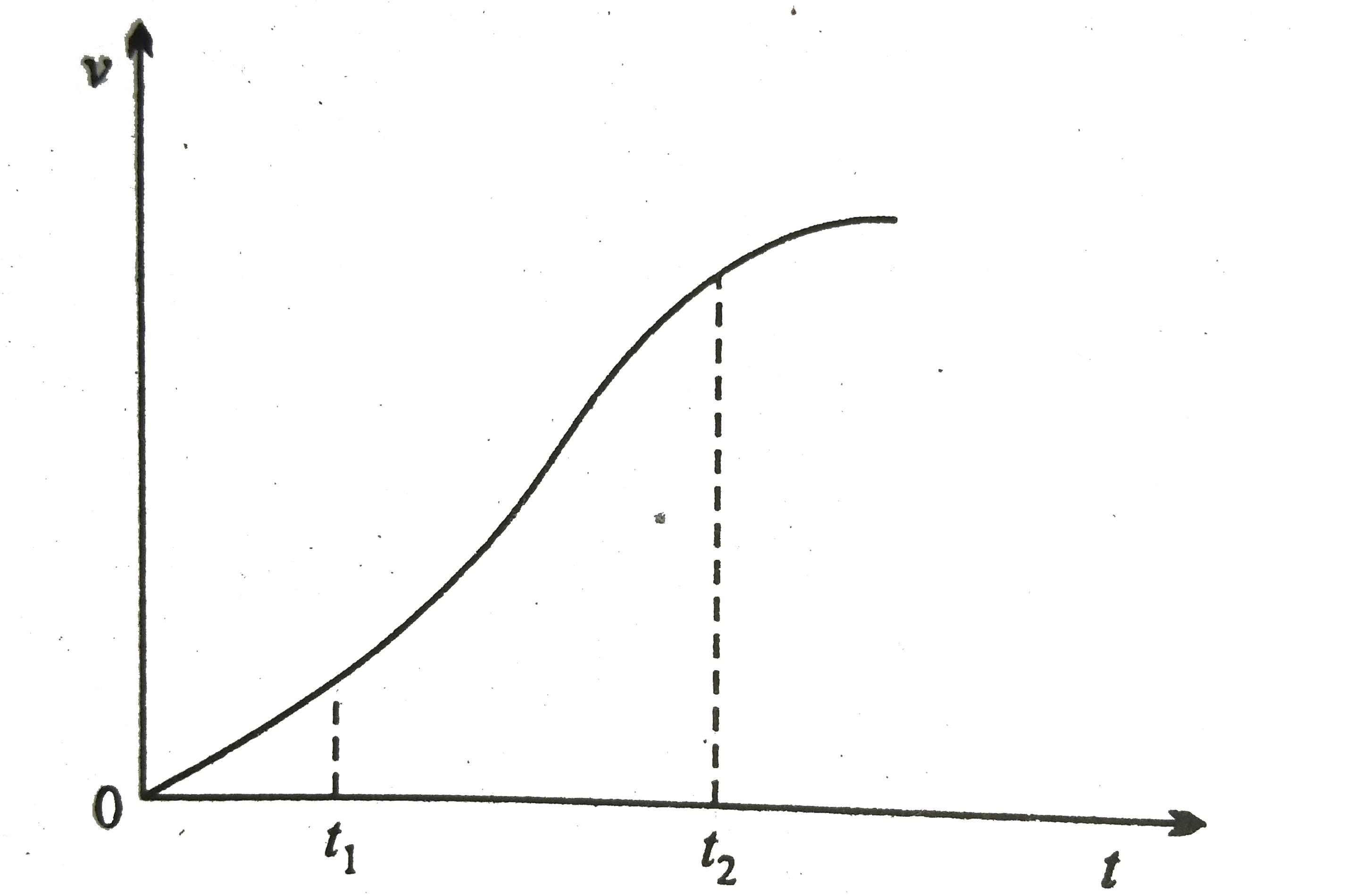
नीचे दिये सूत्रों में t1 से t2 तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन-से सूत्र सही हैं -
(i) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(ii) v(t2)=v(t1)+a(t2−t1)
(iii) vaverage=[x(t2)−x(t1)]/(t2−t1)
(iv) vaverage=[v(t2)−v(t1)]/(t2−t1)
(v) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(vi) x(t2)−x(t1)=t− अक्ष तथा दिखाई गाड़ी बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल ।
View Solutionएकविमीय गति में किसी कण का वेग - समय ग्राफ चित्र में दिखाया गया है-
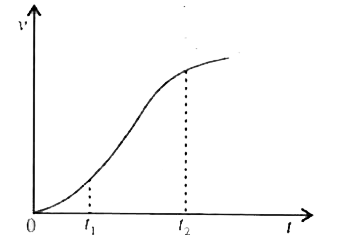
दिए सूत्रों में t1 से t2 तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन - से सूत्र सही हैं
(i) x(t2)=x(t1)+v(t1)(t2−t1)+(1/2)a(t2−t1)2
(i8i) v(t2)=v(t1)+a(t2−t1)
(iii) vaverage=[x(t2)−x(t1)]/(t2−t1)
(iv) aaverage=[v(t2)−v(t1)]/(t2−t1)
(v) x(t2)=x(t1)+vaverage(t2−t1)+(1/2)aaverage(t2−t1)2
(vi) x(t2)−x(t1)=t− अक्ष तथा दिखाई गई बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल |
View SolutionFollowing are four different relation about displacement,velocity and acceleration for the motion of a particle in general.Choose the incorrect one (S). a) V_(av)=(1)/(2)[v(t_(1))+v(t_(2))] b) V_(av)=(r(t_(2))-r(t_(2)))/(t_(2)-t_(1)) c)r= (1)/(2)(v(t_(2))-v(t_(1))(t_(2)-t_(1)) d) a_(av)=(v(t_(2))-v(t_(1)))/(t_(2)-t_(1))
View SolutionSuppose
(x+a)n=T0+T1+T2+…+Tn
Then (T0−T2+T4−…)2+(T1−T3+T5−….)2 is equal to
View SolutionFor any arbitrary motion in space, which of the following relations are true?
a) vaverage=(1/2)(v(t1+v(t2)
b) vaverage=[r(t2)−rt1t2−t1
v(t)=v(0)+at
d) aaverage=[v(t2)−vt1t2−t1
The average stands for average of the quantity over time interval t1 to t_(2)
View SolutionIf t_(1)+t_(2)+t_(3)=-t_(1)t_(2)t_(3) , Then points [at_(1)t_(2),a(t_(1)+t_(2))] , [at_(2)t_(3),a(t_(2)+t_(3))] And [at_(3)t_(1),a(t_(3)+t_(1))] The perpendicular of the triangle with vertices will be
View SolutionThe velocity-time graph of a particle in one-dimensional motion is shown in Fig.
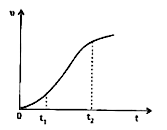
Which of the following formulae are correct for describing the motion of the particle over the time-interval t1 to t2 :
a) x(t2)=x(t1)+v(t1)(t2−t1)+(12)a(t2−t1)2
b) v(t2)=v(t1)+a(t2−t1)
c) vaverage=(x(t2)−x(t1))/(t2−t1)
d) vaverage=(v(t2)−v(t1))/(t2−t1)
e) x(t2)=x(t1)+vaverage(t2−t1)+(12)aaverage(t2−t1)2
f) x(t2)=x(t1) = area under the v - t curve bounded by the t-axis and the dotted line shown.
View Solution
