Question

वृत्त $x^2+y^2=4$ के प्रथम चतुर्थेाश में स्थित भाग और सरल रेखा $y=x$ तथा x - अक्ष से घिरे भाग का क्षेत्रफल ज्ञात कीजिए ।

Explanation

`x^(2) + y^(2) = 4 rArr sqrt(2^(2) -x^(2))" "....(1)`
`y = x " "(2)`
दोनों समीकरणो को हल करने पर प्रतिच्छेद बिन्दु `Q(-sqrt(2), - sqrt(2))` और `P(sqrt(P),sqrt(P))` प्राप्त होता है।
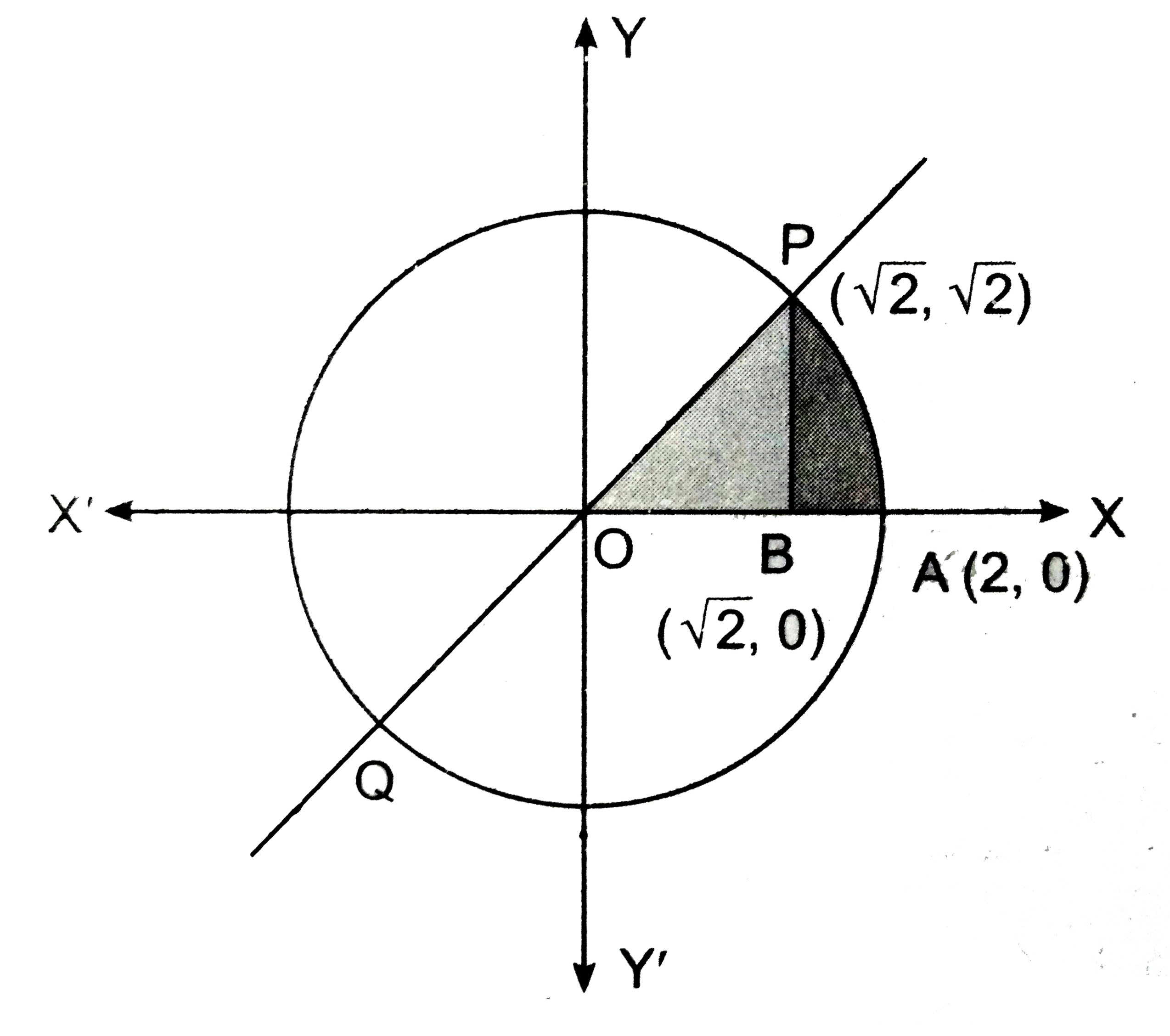प्रथम चुतूर्थाश में `PB bot OX`.
दिये वृत्त का केन्द्र (0,0) और त्रिज्या 2 मात्रक है
अब अभीष्ट क्षेत्रफल
= OBP का क्षेत्रफल +BAP का क्षेत्रफल
`int _(0) ^(sqrt(2)) x dx + int_(sqrt(2))^(2) sqrt(2^(2) - x^(2)) dx`
` = [(x^(2))/(2)]_(0)^(sqrt(2)) +[(x)/(2)sqrt(2^(2) - x^(2)) + (2^(2))/(2)sin^(-1).(x)/(2)]_(sqrt(2))^(2)`
`=(1-0)+[(0+ 2 sin^(-1)1)-(sqrt(2)/(2). sqrt(2)+ 2sin^(-1).(1)/(sqrt(2)))]`
` = 1 + 2.(pi)/(2) - 1-2.(pi)/(4)`
` = (pi)/(2)` वर्ग मात्रक