समाकलन विधि का उपयोग करते हुए बक्र |x|+|y| = 1 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
[संकेत : आवश्यक क्षेत्र, रेखाओं x+y=1,x−y=1,−x+y=1 एवं −x−y=1 से घिरा है।
दिया गया वक्र, |x| + |y| = 1
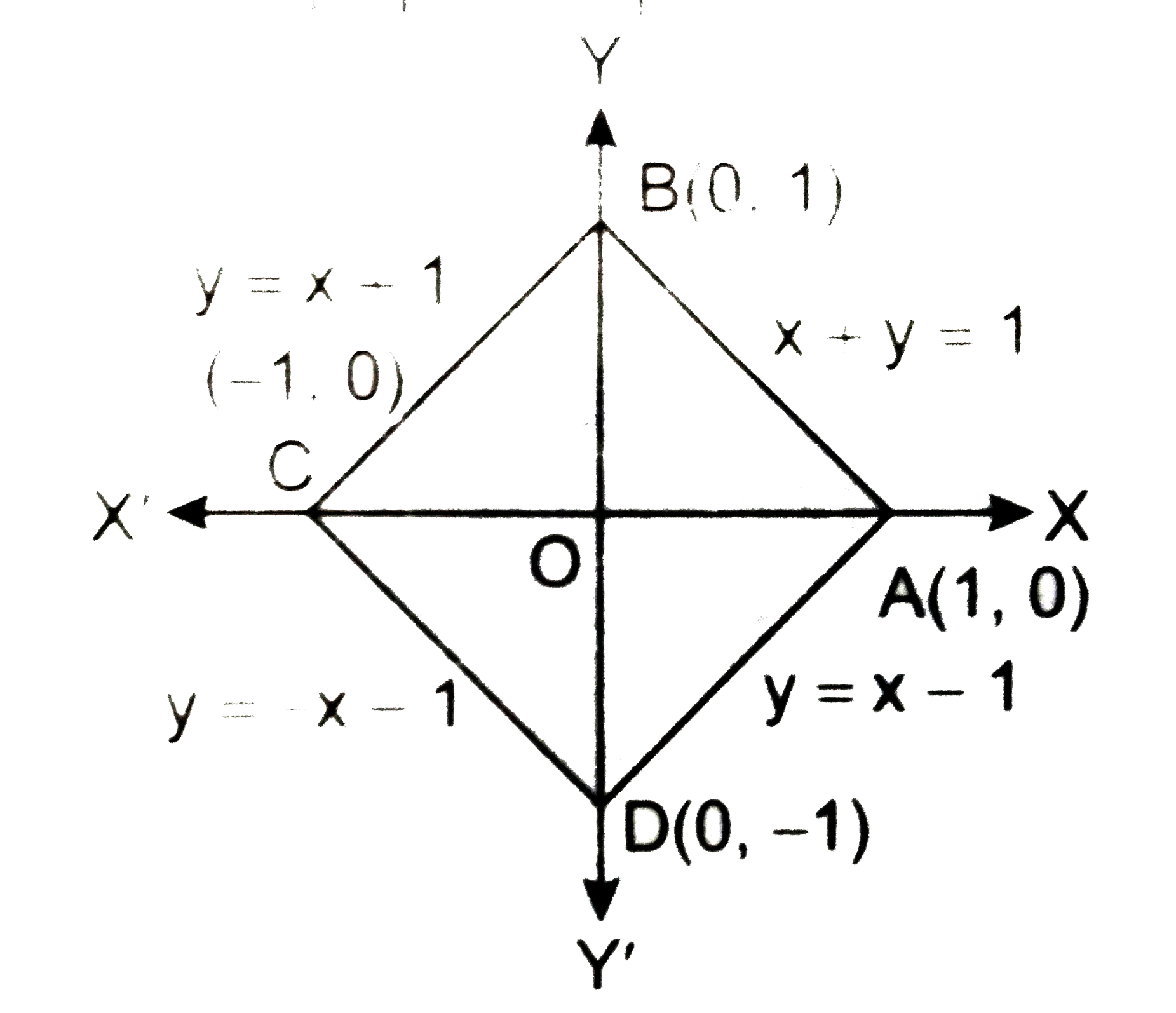
प्रथम चतुर्थांश में, (x>0,y>0) तब, रेखा AB, x + y = 1 है।
द्वितीय चतुर्थांश में, (x<0,y>0) तब, रेखा BC, -x + y = 1 है
तृतीय चतुर्थांश में, (ac<0,y<0) तब, रेखा CD, x-y = 1 है।
चतुर्थ चतुर्थांश में, (x>0,y<0) तब, रेखा DA, x - y = 1 हैं।
चूँकि, ABCD एक वर्ग है ।
अत: अभीष्ट क्षेत्रफल = 4× (प्रथम चतुर्थांश में छायांकित भाग का क्षेत्रफल )
=4∫10(1−x)dx
=4[x−x22]10=4[(1−12)−0]
=2 वर्ग इकाई
Topper's Solved these Questions
Similar Questions
परवलय x2=4y और वृत्त 4x2+4y2=9 के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solution1x−x3
View Solutionमान लीजिए कि f:R→R,f(x)=10x+7 द्वारा परिभाषित फलन है । एक ऐसा फलन g:R→R ज्ञात कीजिए जिसके लिए gof=fog=IR हो ।
View Solutionवक्र y=logx,x−अक्ष,x=1/2तथाx=3/2 से घिरे भाग का क्षेत्रफल ज्ञात कीजिए।
View Solutionवक्रो y=√5−x2तथा y = | x - 1 | से सीमाबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिये |
View Solutionनिश्चित समाकलन की सहायता से रेखाओं y=|x+1|,x=−3,x=1 और X-अक्ष से घिरे भाग का क्षेत्रफल ज्ञात: कीजिए।
View Solutionपरवलय y=4−x2 तथा x -अक्ष से परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
View Solutionवकों y2=2x+1 तथा x=y+1 से घिरे क्षेत्र का क्षेत्रफल है :
View Solution{(x,y):y2≤2x तथा y≥4x−1} द्वारा परभाषित क्षेत्र का क्षेत्रफल है :
View Solutionदीर्घवृत्त x24+y29=1 से घिरे क्षेत्र का क्षेत्रफल 6π2 वर्ग मात्रक है।
View Solutionसरल रेखा y=2x,X− अक्ष तथा कोटियों x=0 और x=3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
View Solutionवृत्त x2+y2=a2 तथा वक्र y=|x| से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionप्रथम चतुर्थांश में रेखाओं x = a, y = a तथा x2+y2=a2 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionवक्र y=2√x तथा x=0,x=1 द्वारा परिबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutiony = |x|, x= - 3, x = 1 व x-अक्ष से परिबध्द क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solutionवृत्त x2+y2=16 तथा परवलय x2=6y से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View Solution
