सदिश विधि द्वारा सिद्ध कीजिए कि sin(α−β)=sinαcosβ−cosαsinβ
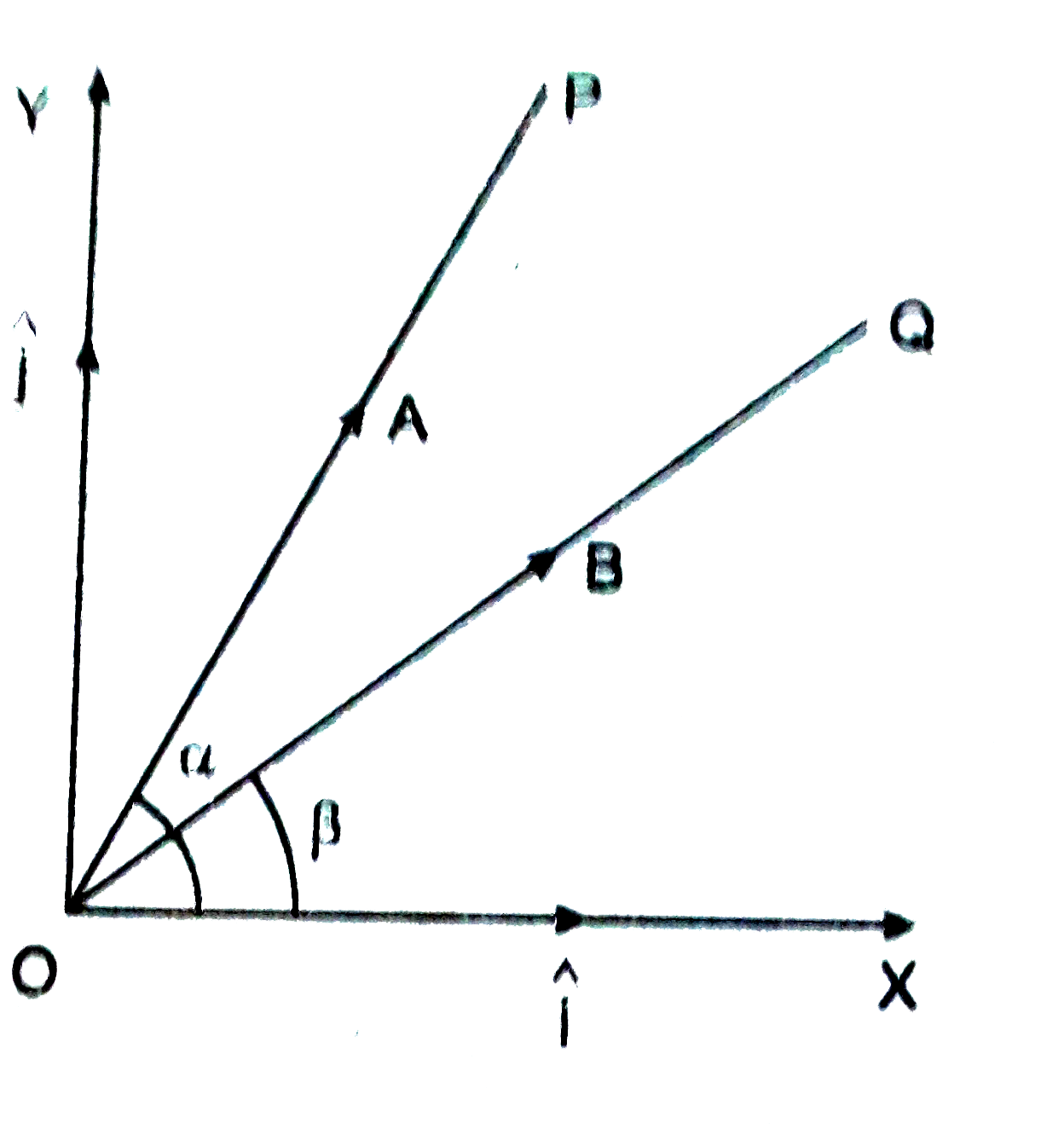
माना ˆi और ˆj क्रमश : OX और OY दिशा में एकांक सदिश है OP और OQ रेखाएँxy - समतल में स्थित है जो OX से क्रमश : α और β कोण बनती है
∴∠POQ=α−β
यदि OP दिशा में एकांक सदिश −−→OA है , तो
−−→OA=cosα.ˆi+sinα.ˆj
इसी प्रकार यदि OQ दिशा में एकांक सदिश −−→OB है तो
−−→OB=cosβ.ˆi+sinβ.ˆj
∴−−→OB×−−→OA=(cosβ.ˆi+sinβ.ˆj)×(cosα.ˆi+sinα.ˆj)
=∣∣∣(ˆi,ˆj,ˆk),cosβ,sinβ,0cosα,sinα,0∣∣∣
=(sinα.cosβ−cosαsinβ)ˆk .... (1)
सदिश गुणन की परिभाषा से
−−→OB×−−→OA=∣∣∣−−→OB∣∣∣∣∣∣−−→OA∣∣∣sin(α−β).ˆk
=1×1×sin(α−β).ˆk
=sin(α−β).ˆk
∴ समीकरण (1) और (2) से
sin(α−β).ˆk=(sinαcosβ−cosαsinβ).ˆk
⇒sin(α−β)=sinαcosβ−cosαsinβ
Topper's Solved these Questions
- सदिश एवं सदिशों का गुणन BOOK - NOOTAN HINDICHAPTER - सदिश एवं सदिशों का गुणन EXERCISE - प्रश्नवाली 10 A
14 Videos
- सदिश एवं सदिशों का गुणन BOOK - NOOTAN HINDICHAPTER - सदिश एवं सदिशों का गुणन EXERCISE - प्रश्नवाली 10 B
11 Videos
- सततता और अवकलनीयता BOOK - NOOTAN HINDICHAPTER - सततता और अवकलनीयता EXERCISE - विविध प्रश्नावली
23 Videos
- समाकलन BOOK - NOOTAN HINDICHAPTER - समाकलन EXERCISE - विविध प्रश्नावली
44 Videos
Similar Questions
निम्नलिखित मापो को अदिश और सदिश राशि के रूप में वर्गीकृत कीजिए
View Solutionयदि बिन्दुओ A और B के स्थिति सदिश क्रमश : →a और →b है, तो AB के मध्य - बिंदु का स्थिति सदिश ज्ञात कीजिए ।
View Solutiondydx ज्ञात कीजिए|
(3x2−9x+5)9
View Solution1x−x3
View SolutionEvaluate ∣∣ ∣ ∣∣cosαcosβcosαsinβ−sinα−sinβcosβ0sinαcosβsinαsinβcosα∣∣ ∣ ∣∣
View Solution∣∣ ∣ ∣∣cosαcosβcosαsinβ−sinα−sinβcosβ0sinαcosβsinαsinβcosα∣∣ ∣ ∣∣
View SolutionEvaluate: =|cosαcosβcosαsinβ−sinα−sinβcosβ0sinαcosβsinαsinβcosα|
View SolutionFind the value of, cos alpha cos beta, cos alpha sin beta, -no alpha-sin beta, cos beta, 0 sin alpha cos beta, sin alpha sin beta, cos alpha] |
View Solution∣∣ ∣ ∣∣cosαcosβcosαsinβ−sinα−sinβcosβ0sinαcosβsinαsinβcosα∣∣ ∣ ∣∣ का मान ज्ञात कीजिए!
View Solutionसिद्ध करे की (sinα.cosβ+cosα.sinβ)2+(cosα.cosβ−sinα.sinβ)2=1
View Solution∣∣ ∣ ∣∣cosαcosβcosαsinβ−sinα−sinβcosβ0sinαcosβsinαsinβcosα∣∣ ∣ ∣∣ का मान ज्ञात कीजिए।
View SolutionIfxcosα+ysinα=xcosβ+ysinβthen
sinα−cosα−sinβ+cosβsinα+cosα−sinβ−cosβ=
View SolutionEvaluate ⎡⎢⎣cosαcosβcosαsinβ−sinα−sinβcosβ0sinαcosβsinαsinβcosα⎤⎥⎦=0
View SolutionEvaluate ∣(cosαcosβ,cosαsinβ,−sinα),(−sinβ,cosβ,0),(sinαcosβ,sinαsinβ,cosα)|}=0
View SolutionEvaluate ∣(cosαcosβ,cosαsinβ,−sinα),(−sinβ,cosβ,0),(sinαcosβ,sinαsinβ,cosα)|}=1
View SolutionEvaluate ⎡⎢⎣cosαcosβcosαsinβ−sinα−sinβcosβ0sinαcosβsinαsinβcosα⎤⎥⎦=0
View Solution
