यदि →a=→b+→c, तब क्या यह सत्य है कि |→a|=∣∣→b∣∣+|→c| ? अपने उत्तर कि पुष्टि कीजिए ।
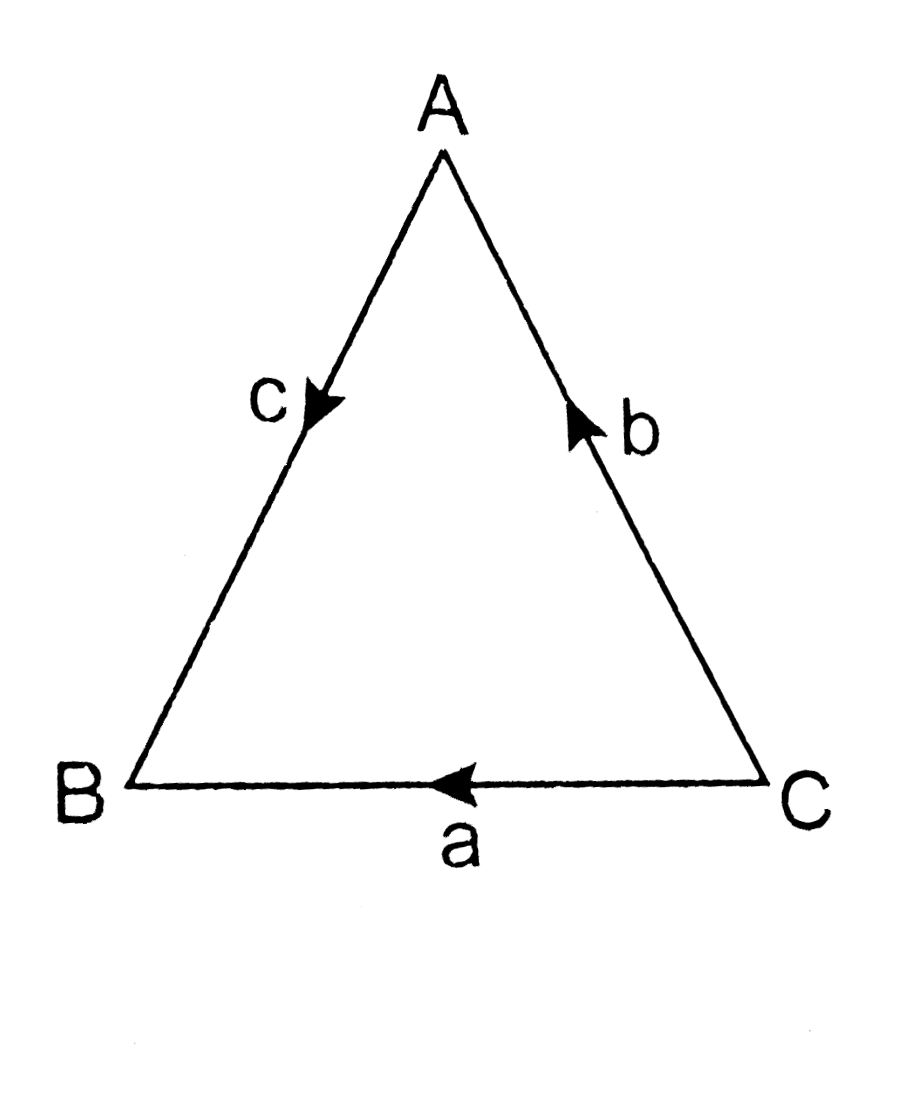
ΔABC में माना −−→CB=→a ,
−−→CA=→b तथा −−→AB=→c
अब योग के त्रिभुज नियम से →a=→b+→c
स्पष्टतया यह ज्ञात कि |→a|,∣∣→b∣∣ तथा |→c|=ΔABC की भुजाएँ है तथा हम यह भी जानते है कि त्रिभुज कि किन्ही दो भुजाओ का योग तीसरी भुजा से बड़ा होता है ।
∴|→a|<∣∣→b∣∣+|→c|
अंत : यह सत्य नहीं है कि |→a|=∣∣→b∣∣+|→c|
Topper's Solved these Questions
Similar Questions
यदि →a=ˆi−7ˆj+7ˆk और →c=3ˆi−2ˆj+2ˆk तो ∣∣→a×→b∣∣ ज्ञात कीजिए ।
View Solutiondydx ज्ञात कीजिए|
(3x2−9x+5)9
View Solution1x−x3
View SolutionIf→a,→b,→c are three mutually perpendicular vectors, then the vector which is equally inclined to these vectors is (A) →a+→b+→c (B) →a|→a|+→b∣∣→b∣∣+→/|→c| (C) →a|→a|2+→b∣∣→b∣∣2+→c|→c|2 (D) |→a|→a−∣∣→b∣∣→b+|→c|→c
View Solutionयदि →a,→b,→c तीन सदिश इस प्रकार हैं कि →a.→b=→a.→c,→a×→b=→a×→c तथा →a≠0 तो दिखाइए कि →b=→c.
View SolutionIf →a=ˆi+ˆj+ˆk,→b=ˆi−ˆj+ˆk,→c=ˆi+2ˆj−ˆk, then the value of ∣∣ ∣ ∣∣→a⋅→a→a⋅→b→a⋅→c→b⋅→a→b⋅→b→b⋅→c→c⋅→a→c⋅→b→c⋅→c∣∣ ∣ ∣∣ is equal to :
View Solutionयदि △ABC के शीर्ष A,B,C के स्थिति सदिश →a,→b,→c हो तो दिखाइए कि △ABC का क्षेत्रफल 12∣∣→a×→b+→b×→c+→c×→a∣∣ बिंदु →a,→b,→c संरेख है यदि :
→a×→b+→b×→c+→c×→a=→0
View Solutionयदि →a+→b+→c=0 तो सिद्ध कीजिए कि →a×→b=→b×→c=→c×→a इस परिमाण का ज्यामितीय विमोचन कीजिए |
View Solutionयदि [→a×→b→b×→c→c×→a]=λ[→a→b→c]2 तो λ बराबर है |
View Solutionसिद्ध कीजिए कि [→a×→b→a×→c→d]=[→a.→d][→a→b→c]
View Solutionयदि →a,→b,→c समान परिमाण के परस्पर लम्ब सदिश हो तो सिद्ध कीजिए कि सदिश →a+→b+→c सदिशों →a,→b और →c के साथ बराबर कोण बनाता है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solutionसिद्ध कीजिए कि [→a×→b→a×→c→d]=(→a.→d)[→a→b→c]
View Solutionयदि →a,→b,→c इस प्रकार कि इकाई सदिश है कि →a.→b=0=→a.→c तथा →b और →c के मध्य का कोण π6 है , तब सिद्ध कीजिए कि →a=±2(→b×→c)
View Solutionमाना →a=ˆi−2ˆj+3ˆk , यदि एक सदिश →b इस प्रकार है कि →a.→b=∣∣→b∣∣2 तथा ∣∣→a−→b∣∣=√7, तब ∣∣→b∣∣=
View Solutionयदि →a=→b+→c, तब →a.(→b×→c) बराबर है -
View Solution
