Question

चित्र में दो गुटके दिखाए गए हैं जिनके द्रव्यमान m तथा M है। ये गुटके एक घर्षणरहित क्षैतिज सतह पर रखे हैं तथा k स्प्रिंग नियतांक वाले एक स्प्रिंग से जुड़े हैं। प्रारंभ में स्प्रिंग अपनी स्वाभाविक लंबाई में है तथा गुटके स्थिर हैं। अब एक अचर बल F, द्रव्यमान M वाले गुटके पर लगना प्रारंभ करता है। स्प्रिंग की लंबाई में अधिकतम वृद्धि निकालें।

Explanation

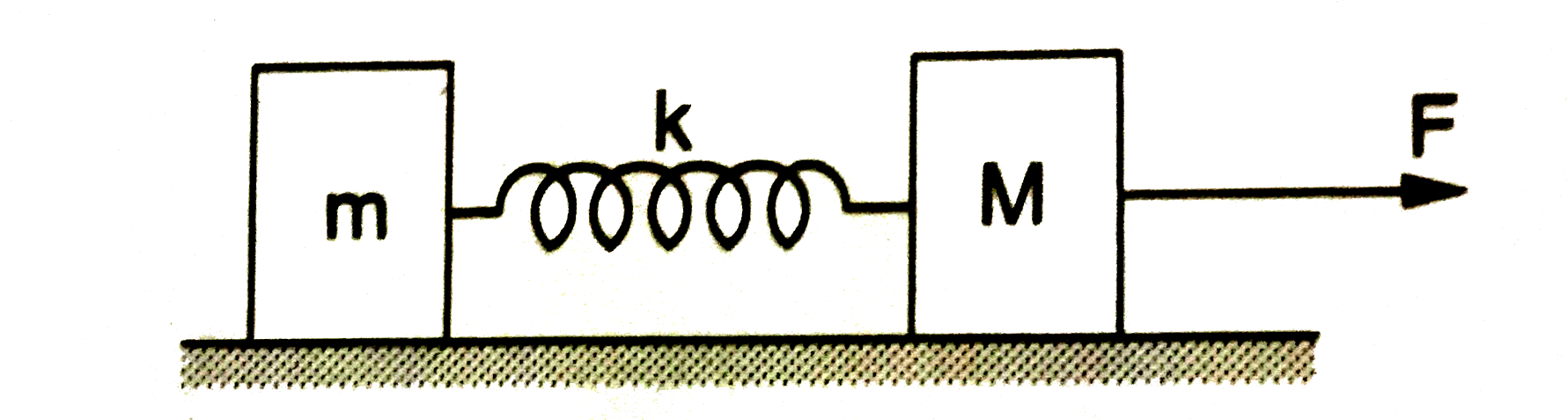
जब तक दाहिना गुटका अधिक वेग से तथा बायाँ गुटका कम वेग से चलता रहेगा, तब तक स्प्रिंग की लंबाई बढ़ती रहेगी। स्प्रिंग की लंबाई अधिकतम तब होगी, जब दोनों गुटकों के वेग बराबर हो जाएँगे।
मान लें कि ? समय में बायाँ गुटका xदूरी विस्थापित होता है। और दाहिना गुटका 3 दूरी विस्थापित होता है। तब स्प्रिंग की लंबाई में वृद्धि होगी। स्प्रिंग में तनाव k(x, -x) होगा। अतः, । समय पर दाहिने गुटके पर बल %3D F -k(x) -~x1 ) तथा बाएँ गुटके पर बल %3 k(xz - x1) होगा।
अतः उनकी गति के समीकरण होंगें,
` " "F-k(x_2-x_1)= M(dv_2)/(dt) " "...(i)`
तथा ` " "k(x_2-x_1) =m (dv_1)/(dt) " "...(ii)`
समीकरण (i ) को m से तथा समीरकण (ii ) को M से गुणा करके घटाने पर,
` " "mF-(m+M)k (x_2-x_1)=Mm(d)/(dt) (v_2-v_1)`
`x_2-x_1` को x तथा `v_2-v_1` को v लिखे|तब इस समीकरण को इस प्रकार लिख सकते है,
` mF-(m+M)kx=Mm(dv)/(dt) =Mm (dv)/(dx) =Mm(vdv)/(dx)`
या ` " "[mF-(m+M) kx ]dx =Mmvdv `
प्रारम्भ में ` x_1 =0 ,x_2 =0,` अतः ` x= x_2 -x_1 =0`
साथ ही `v_1 =0 ,v_2 =0` अतः ` " "v=v_2-v_1 =0`
अतः,` int _0^(x)[mF -(m+M) kx ]dx =mMint _0^(v) vdv `
या ` " "mFx-(m+M)k(x^(2))/(2) =(1)/(2) Mmv^(2)`
स्प्रिंग की अधिकतम लम्बाई के लिए v =0
या ` " "[mF-(m+M)k(x)/(2) ]x=0`
या ` " "x= (2mF)/((m+M)k)` यही स्प्रिंग की लम्बाई में अधिकतम वृद्धि हुई|