एक चिकने क्षैतिज तल पर m तथा M द्रव्यमान के दो गुटके पकड़कर रखे गए हैं। इन गुटकों के बीच एक नगण्य भार वाला स्प्रिंग दबाकर रखा गया है (चित्र 15.5W)। जब गुटकों को छोड़ दिया जाता है, तो वे विपरीत दिशाओं में गति करने लगते हैं और जब स्प्रिंग अपनी स्वाभाविक स्थिति में आ जाता है, तो गुटके उससे संपर्क छोड़ देते हैं। यदि स्प्रिंग का प्रारंभिक संपीडन x तथा स्प्रिंग नियतांक k हो, तो गुटकों के अंतिम वेग क्या होंगे?
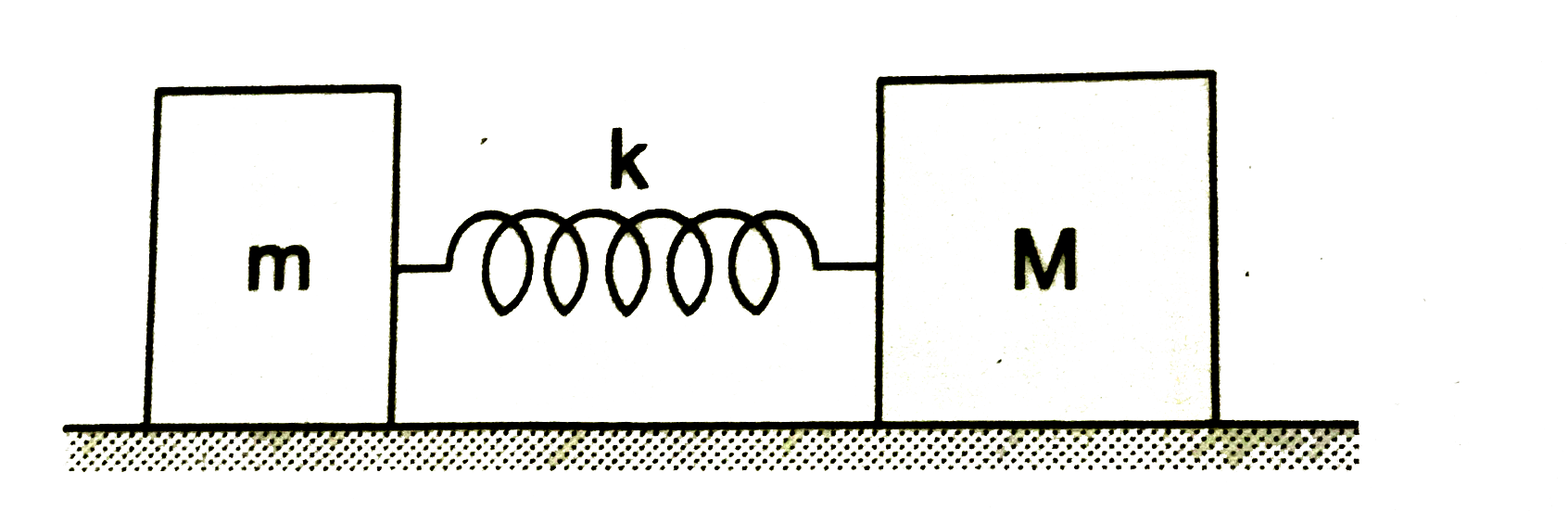
दोनों गुटकों तथा स्प्रिंग को मिलाकर निकाय मानें। इस निकाय पर क्षैतिज दिशा में कोई बाहरी बल नहीं लग रहा है। अतः, इसका संवेग स्थिर रहेगा। प्रारंभ में गुटके तथा स्प्रिंग स्थिर हैं, अतः कुल संवेग शून्य है। अंत में यदि M द्रव्यमान का गुटका V वेग से तथा mm द्रव्यमान का गुटका D वग से चले, तो कुल संवेग MV - mu होगा। स्प्रिंग का भार नगण्य होने के कारण उसका संवेग शून्य लिया गया है। अतः,
MV−mv=0
या V=mMv. ...(i)
प्रारंभिक में निकाय की कुल यांत्रिक ऊर्जा =12kx2
अंत में निकाय की कुल यांत्रिक ऊर्जा =12mv2+12MV2
चूँकि निकाय पर कोई बाहरी बल कार्य नहीं कर रहा है, इसलिए यांत्रिक ऊर्जा में कोई परिवर्तन नहीं होगा|
अतः 12kx2=12mv2+12MV2 ...(ii)
समीकरण (i ) का उपयोग करने पर,
12kx2=12mv2+12m2Mv2
kx2=mv2(1+mM)
अतः v=√kMM(M+m)x
तथा V=√kmM(M+m)x
Topper's Solved these Questions
- BOOK - HC VERMA HINDICHAPTER - संवेग- संरक्षण का सिद्धांत, टक्कर EXERCISE - विचार हेतु प्रश्न10videos
संवेग- संरक्षण का सिद्धांत, टक्कर
- BOOK - HC VERMA HINDICHAPTER - संवेग- संरक्षण का सिद्धांत, टक्कर EXERCISE - सटीक उतरवाले प्रश्न - I (सही उतर का चयन करें)11videos
संवेग- संरक्षण का सिद्धांत, टक्कर
- BOOK - HC VERMA HINDICHAPTER - संवेग- संरक्षण का सिद्धांत, टक्कर EXERCISE - अभ्यास के प्रश्न57videos
संवेग- संरक्षण का सिद्धांत, टक्कर
- BOOK - HC VERMA HINDICHAPTER - वृत्त में गति EXERCISE - अभ्यास के प्रश्न25videos
वृत्त में गति
- BOOK - HC VERMA HINDICHAPTER - सदिश राशियों का गणित EXERCISE - अभ्यास के प्रश्न16videos
सदिश राशियों का गणित
Similar Questions
आप किसी रेलवे स्टेशन पर ट्रेन की प्रतिक्षा कर रहे है। आपका 3 साल का भाई प्लैटफॉर्म पर रखे एक संद्रिक पर चढ़कर पलैटफॉर्म पर कूद रहा है। संवेग-संरक्षण के अनुसार संद्रक पीछे क्यो नहीं जाती?
04:32View Solutionनिम्नलिखित दो वकतत्यों को देखें.
(A) एक निकाय को रेखीय संबग अचर रहता है।
(B) एक निकाय का द्रव्यमान केंद्र स्थिर रहता है।44:26View Solution1.0 kg तथा 4.0kg द्रव्यमानों के दो कणों की गतिज ऊर्जाएँ बराबर हैं। इनके रैखिक संवेगों का अनुपात ज्ञात कीजिए।
View Solutionधरती और चंद्रमा के बीच की दुरी 3.85×105km है तथा चंद्रमा को धरती का चक्कर लगाने में 27.3 दिन लगते है। इतनी जानकारी से चंद्रमा का त्वरण निकालें ।
View Solutionएक वेक्टर →A x -अक्ष से 45∘ का कौन बनाता है ओर उसी ओर घूमते हुए दूसरा वेक्टर →B x -अक्ष से 135∘ का कौन बनता है। इन वेक्टरो के परिमाण क्रमशः 4 इकाई ओर 4 इकाई है।→A तथा →B का परिणामी निकाले।
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionसंपर्क में रखे गुटकों की गति
View Solutionजब भी कवि के पिता काम करते हैं, तो उनके कार्य करने के ढंग में क्या है?
View Solutionजब धातु M को NaOH के साथ उपचारित किया जाता है, तो एक श्वेत जिलेटिन जैसा अवक्षेप 'X' प्राप्त होता है, जो NaOH के आधिक्य में घुलनशील होता है। यौगिक 'X' प्रबल रूप से गर्म करने पर एक ऑक्साइड देता है जिसका उपयोग वर्णलेखिकी में एक अधिशोषक के रूप में किया जाता है। धातु 'M' है:
View Solution300 K पर N_2O_4 (g) के एक मोल को एक वायुमंडलीय दाब के अंतर्गत एक बंद पात्र में रखा जाता है। जब इसको 600 K तक गर्म किया जाता है, तो द्रव्यमानानुसार 20% N_2O_4(g) का NO_2 (g) में अपघटन हो जाता है। परिणामी दाब ( atm में) है:
View Solutionजब AgNO_(3) के विलयन को आधिक्य में CoCl_(3).XNH_(3) विलयन के 1M में मिलाया जाता है, तो AgCI के एक मोल का निर्माण होता है? 'X' का मान क्या है? (माना लीजिए कि उपसहसंयोजन संख्या 6 है।)
View Solutionजब logk और 1/T के बीच एक आलेख आलेखित किया जाता है, तो हमें एक आलेख प्राप्त होता है, जैसा कि नीचे दर्शाया गया है आलेख में ढाल का मान क्या है?
View Solutionनिम्नलिखित अणु के लिए,
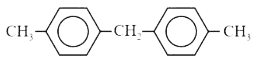
जब किसी एक हाइड्रोजन को क्लोरीन परमाणु द्वारा प्रतिस्थापित कर दिया जाता है, तो कितने संरचनात्मक समावयवी संभव हैं?View Solutionजब शुष्क ईथर में आयोडोबेन्जीन को सोडियम के साथ उपचारित किया जाता है, तो उत्पाद है:
View Solutionजब सल्फ्यूरिक अम्ल का एक मोल बम कैलोरीमीटर में जिंक चूर्ण के एक मोल के साथ अभिक्रिया करता है, तो ΔU और w किसके संगत होते हैं:
View Solutionजब CO_(2) को जल में विलेय किया जाता है तो विलयन में उपस्थित प्रजाति है:
View Solution

