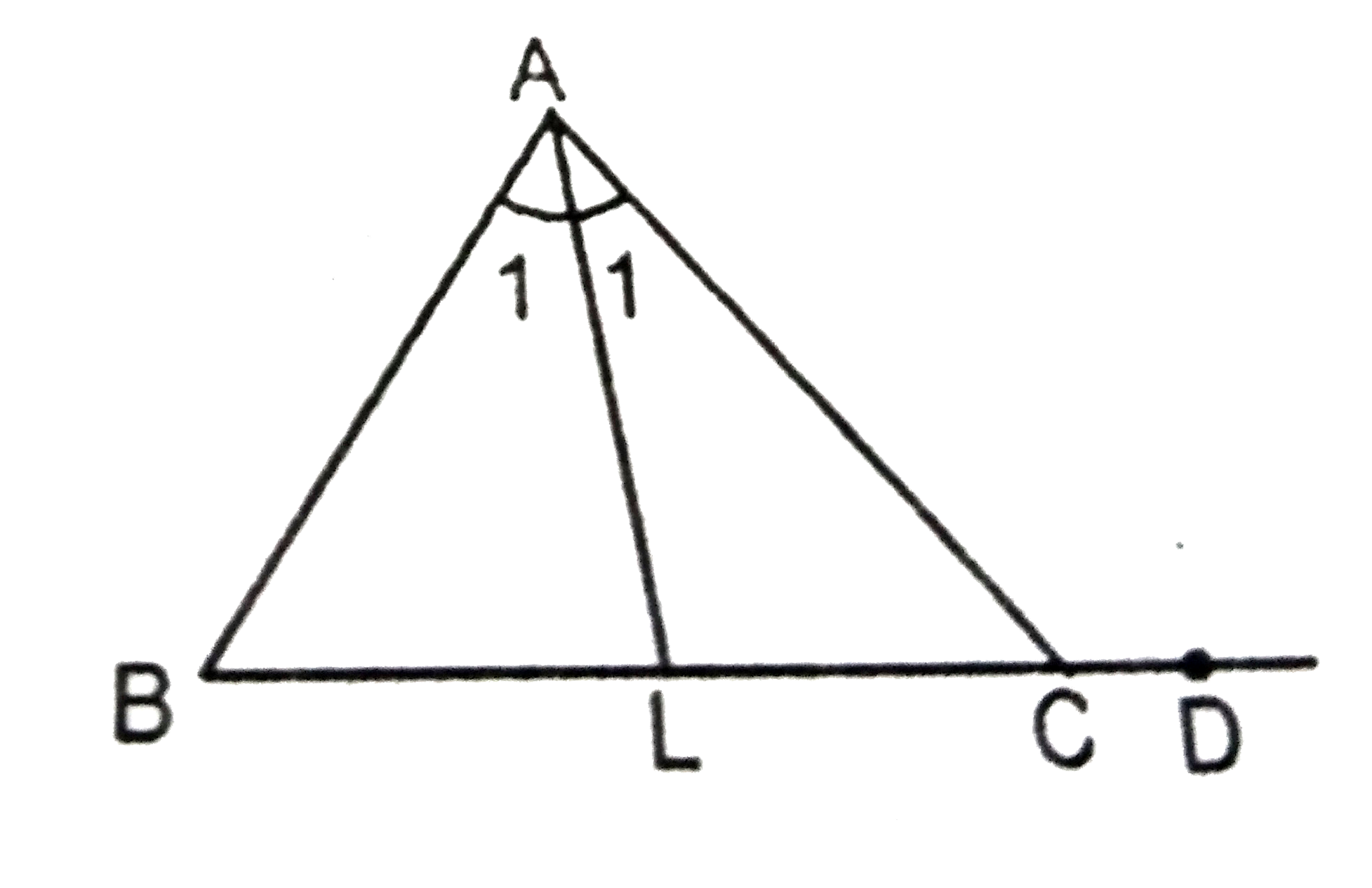
एक त्रिभुज ABC की भुजा BC इस प्रकार बढ़ाई गयी है कि D , किरण BC पर है । ∠A का समद्विभाजक BC पर L में मिलता है तो सिद्ध कीजिए कि ∠ABC+∠ACD=2∠ALC

ΔABC में , यहाँ है,
बाह्रा ∠ACD=∠B+∠A ( बाह्रा कोण प्रमेय द्वारा)
⇒ बाह्रा ∠ACD=∠B+2∠1
(∵AL,∠A का समद्विभाजक है इसलिए, ∠A=2∠1)
⇒∠ACD=∠B=2∠1 ….(1)
ΔABL में ,यहाँ है ,
तथा ∠ALC=∠B+∠BAL
⇒∠ALC=∠ALC=∠B+∠1
⇒2∠ALC=2∠B+2∠1 ....(2)
(2)−(1) से,
=2∠ALC−∠ACD=∠B
⇒2∠ALC=∠ACD+∠B
अतः ∠ACD+∠ABC=2∠ALC
Topper's Solved these Questions
- त्रिभुज एवं उसके गुण BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज एवं उसके गुण EXERCISE - अभ्यास प्रश्न 11.1(अतिलघु उत्तरीय प्रश्न )
7 Videos
- त्रिभुज एवं उसके गुण BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुज एवं उसके गुण EXERCISE - अभ्यास प्रश्न 11.1 (लघु उत्तरीय प्रश्न )
13 Videos
- चतुर्भुर्जBOOK - BALAJI PUBLICATIONCHAPTER - चतुर्भुर्जEXERCISE - स्वमूल्यांकन परिक्षण
29 Videos
- त्रिभुजों की सर्वांगसमता BOOK - BALAJI PUBLICATIONCHAPTER - त्रिभुजों की सर्वांगसमता EXERCISE - स्वमूल्यांकन परीक्षण
15 Videos
Similar Questions
यदि एक त्रिभुज के दो कोण बराबर है तब दोनों की विपरीत भुजा बराबर है या नहीं ?
View Solutionएक त्रिभुज के कोण 2:3:7 के कोण में है । त्रिभुज के प्रत्येक कोण की माप ज्ञात कीजिए।
View Solutionसिद्ध कीजिए की एक समान्तर चतुर्भुर्ज की विपरीत के मध्य बिंदुओं को मिलाने वाली सरल रेखा, समान्तर भुजाओं के अन्य युग्म से समान्तर होती है।
View Solutionरेखा l कोण A की समद्विभाजक है तथा l पर कोई बिंदु B है| BP और BQ बिंदु B से ∠Aकी भुजाओं पर लम्ब है तो दिखाइये कि-

(i) ΔAPB≅ΔAQB
(ii) BP=BQ
View SolutionIf in a DeltaABC,cosAa=cosBb=cosCc, then find the measures of angles A, B, C.
View SolutionThe sides BC of ABC is product to a point D . The bisector of ∠A meets side BC in L . If ∠ABC=300 and ∠ACD=1150, find ∠ALC
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionΔABC की भुजा BC को D तक बढ़ाया जाता है ∠A का समद्विभाजक BC को L पर मिलता है ।
सिद्ध कीजिये कि ∠ABC+∠ACD=2∠ALC
View SolutionΔABC की भुजा BC को D तक बढ़ाया गया है। ∠A का समद्विभाजक BC से L पर मिलता है। सिद्ध करें कि ∠ABC+∠ACD=2∠ALC
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solution
