The sides BC of ABC is product to a point D . The bisector of ∠A meets side BC in L . If ∠ABC=300 and ∠ACD=1150, find ∠ALC
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
Step 1: Identify the given angles
We are given:
- ∠ABC=30∘
- ∠ACD=115∘
Step 2: Apply the Exterior Angle Theorem
According to the Exterior Angle Theorem, the exterior angle (∠ACD) is equal to the sum of the two opposite interior angles (∠A+∠ABC).
∠ACD=∠A+∠ABC
Substituting the known values:
115∘=∠A+30∘
To find ∠A:
∠A=115∘−30∘=85∘
Step 3: Determine the Linear Pair
Since ∠ACL and ∠ACD are a linear pair, we can write:
∠ACL+∠ACD=180∘
Substituting the known value of ∠ACD:
∠ACL+115∘=180∘
To find ∠ACL:
∠ACL=180∘−115∘=65∘
Step 4: Find ∠A at point L
Since AL is the angle bisector of ∠A, we can write:
∠A=12×∠A=42.5∘
Step 5: Apply the Angle Sum Property in Triangle ALC
In triangle ALC, the sum of the angles is 180∘:
∠A+∠C+∠L=180∘
Substituting the known values:
42.5∘+65∘+∠L=180∘
Calculating:
107.5∘+∠L=180∘
To find ∠L:
∠L=180∘−107.5∘=72.5∘
Final Answer
Thus, ∠ALC=72.5∘.
---
We are given:
- ∠ABC=30∘
- ∠ACD=115∘
According to the Exterior Angle Theorem, the exterior angle (∠ACD) is equal to the sum of the two opposite interior angles (∠A+∠ABC).
∠ACD=∠A+∠ABC
Substituting the known values:
115∘=∠A+30∘
To find ∠A:
∠A=115∘−30∘=85∘
Since ∠ACL and ∠ACD are a linear pair, we can write:
∠ACL+∠ACD=180∘
Substituting the known value of ∠ACD:
∠ACL+115∘=180∘
To find ∠ACL:
∠ACL=180∘−115∘=65∘
Since AL is the angle bisector of ∠A, we can write:
∠A=12×∠A=42.5∘
In triangle ALC, the sum of the angles is 180∘:
∠A+∠C+∠L=180∘
Substituting the known values:
42.5∘+65∘+∠L=180∘
Calculating:
107.5∘+∠L=180∘
To find ∠L:
∠L=180∘−107.5∘=72.5∘
Thus, ∠ALC=72.5∘.
Topper's Solved these Questions
Similar Questions
The side BC of ABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC=300and ∠ACD=1150, then ∠ALC= 850 (b) 72120 (c) 1450 (d) none of these
View SolutionThe sides BC of ABC is product to a point D . The bisector of ∠A meets side BC in L . If ∠ABC=300 and ∠ACD=1150, find ∠ALC
View Solution
Knowledge Check
In a quadrilateral ABCD, the bisectors of ∠A and ∠B meet at O. If ∠C=70∘and∠D=130∘, then measure of ∠AOBis
A40∘B60∘C80∘D100∘
If in a DeltaABC,cosAa=cosBb=cosCc, then find the measures of angles A, B, C.
View SolutionD is a point on the side BC of ABC. A line PDQ , though D , meets side AC in P and AB produced at Q . If ∠A=800, ∠ABC=600 and ∠PDC=150 find (i) ∠AQD (ii) ∠APD.
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIn Figure, the bisectors of ∠A and ∠B meet at a point P. If ∠C=1000 and ∠D=500, find the measure of ∠APB
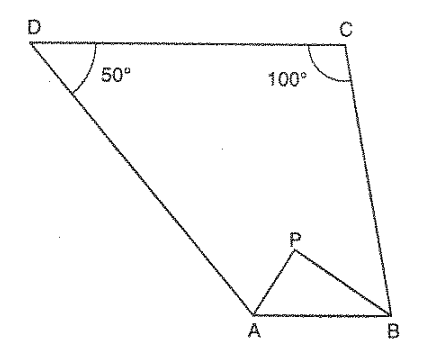
View SolutionIn a ABC, ∠B=1050, ∠C=500, Find ∠A
View SolutionIn Fig.81, side BC of ABC has been produced to D and CEBA. If ∠ABC=650, ∠BAC=550, find ∠ACE, ∠ECD and ∠ACD.
View SolutionIn ABC, ∠B=450, ∠C=550 and bisector of ∠A meets BC at a point D. Find ∠ADB and ∠ADC
View Solution
