की माध्यिकाओं में से एक है तथा का कोई बिंदु है। सिद्ध कीजिए कि ।
में AD एक माध्यिका है।
………..1
माध्यिका, त्रिभुज को बराबर भागों में बांटती है
पुनः में OD एक माध्यिका है।
…………2
समीकरण 1 व 2 से
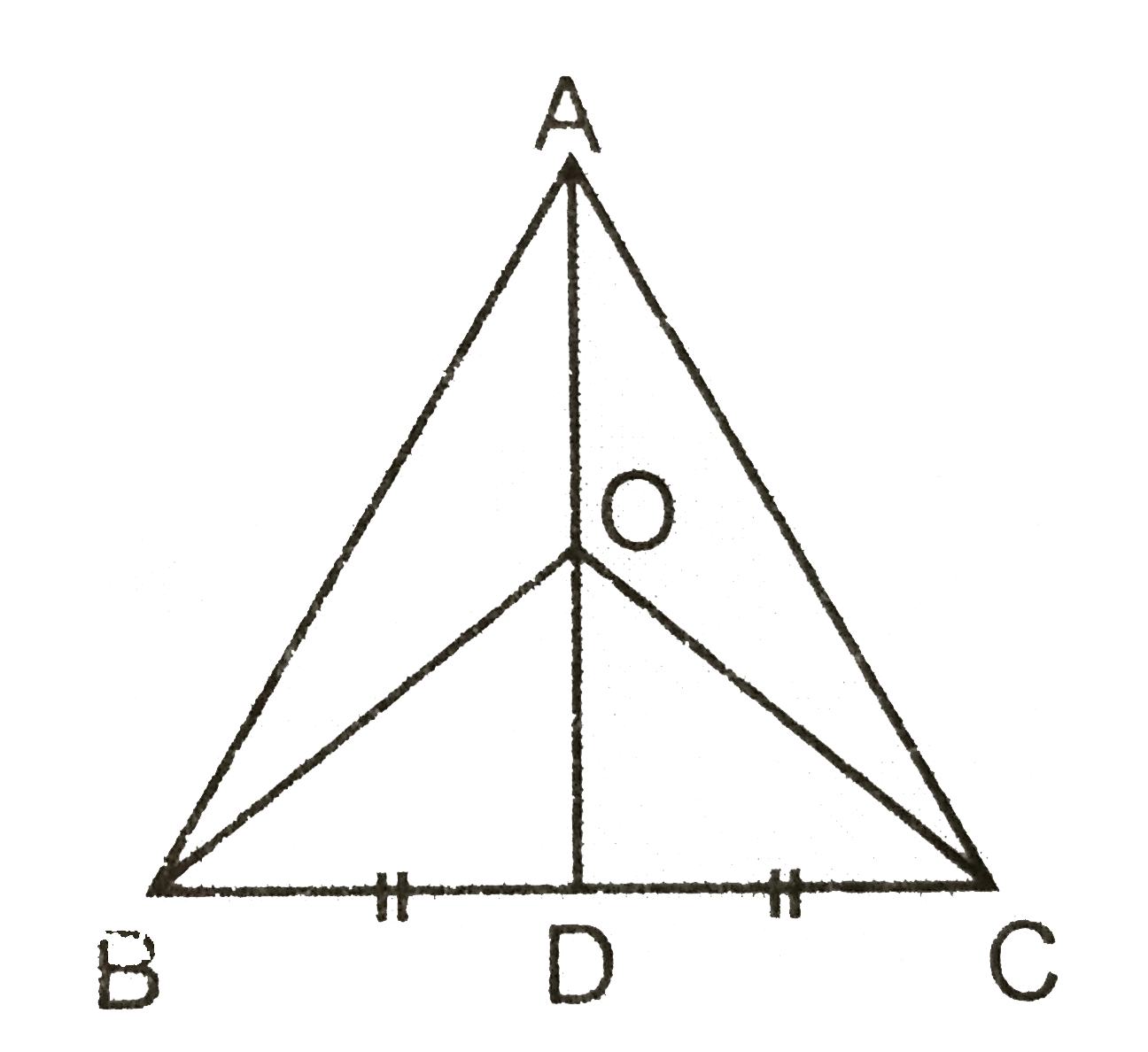
Topper's Solved these Questions
- समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलBOOK - BALAJI PUBLICATIONCHAPTER - समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलEXERCISE - अति लघु उत्तरीय प्रश्न
5 Videos
- समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलBOOK - BALAJI PUBLICATIONCHAPTER - समांतर चतुर्भुज व त्रिभुज के क्षेत्रफलEXERCISE - लघु उत्तरीय प्रश्न
16 Videos
- शेषफल प्रमेय तथा गुणनखण्ड प्रमेय BOOK - BALAJI PUBLICATIONCHAPTER - शेषफल प्रमेय तथा गुणनखण्ड प्रमेय EXERCISE - स्वमूल्यांकन परिक्षण
20 Videos
- सांख्यिकीBOOK - BALAJI PUBLICATIONCHAPTER - सांख्यिकीEXERCISE - स्वमूल्यांकन परीक्षण
17 Videos
Similar Questions
एक समांतर चतुर्भुज के विकर्ण इसे कितने भागों में विभक्त करते हैं?
View Solutionचित्र (i) और (ii) में दिए गये समलम्ब चतुर्भुजों ABCD और PQRS का क्षेत्रफल ज्ञात कीजिए।

View Solutionx3+3x2+3x+1 को 5+2x से भाग करने पर शेषफल ज्ञात कीजिए।
View Solutionतीन सिक्के 30 बार उछाले गये। प्रत्येक बार आये चित् की संख्या निम्न प्रकार लिखी गयी :
0,1,2,2,1,2,3,1,3,0,1,3,1,1,2,2,0,1,2,1,3,0,0,1,1,2,3,2,2,0
उपरोक्त आँकड़ों के लिए एक बारंबारता बंटन सारणी तैयार कीजिए।
View SolutionIn Delta ABC,AD and BE are altitudes.Prove that (ar(Delta DEC))/(ar(Delta ABC))=(DC^(2))/(AC^(2))
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionएक त्रिभुज ABC में मध्यिकाएँ AD ,BE और CF एक बिंदु G से गुजरती है। यदि AD=9 सेमी ,GE=4.2 सेमी और GC=6 सेमी ,तो AG , BE औरFG की लम्बाइयों के मान ज्ञात कीजिए।
View Solutionएक बिंदु इस प्रकार गमन करता है कि उसकी बिंदु (3,4) से दुरी बिंदु (−3,−4) से उसकी दूरी की तिगुनी रहती है । उसका बिन्दुपथ ज्ञात कीजिए ।
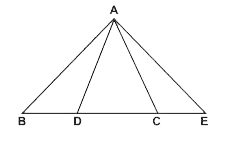
View SolutionIn the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
View SolutionIn triangle ABC , AD is the median and G is a point on AD such that AG : GD = 2 : 1, then ar (triangle BDG): (triangle ABC) is equal to : त्रिभुज ABC में, AD माध्यिका है तथा G, AD पर ऐसा बिंदु है कि AG : GD = 2 : 1 है, तो ar (triangle BDG): (triangle ABC) का मान ज्ञात करें |
View SolutionIn triangle ABC , AD is median and G is the point on AD such that AG: GD = 2: 1, then ar(triangle ABG) :ar(triangle ABC) is equal to : त्रिभुज ABC में, AD मध्यिका है तथा G, AD पर स्थित ऐसा बिंदु है कि AG: GD = 2 : 1 है, तो ar(triangle ABG) :ar(triangle ABC) का मान किसके बराबर होगा ?
View SolutionIn triangle ABC , AD is median and P is the point on AD such that AP : PD = 3 : 4, then ar(triangle APB) :ar(triangle ABC) is equal to : त्रिभुज ABC में, AD मध्यिका है तथा P, AD पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है, तो ar(triangle APB) :ar(triangle ABC) का मान किसके बराबर होगा ?
View SolutionIn triangle ABC ,AD is a median and P is a point on AD such that AP : PD = 3 : 4. Then ar (triangle BPD): ar (triangle ABC) is equal to: त्रिभुज ABC में, AD एक माध्यिका है और P, AB पर स्थित ऐसा बिंदु है कि AP : PD = 3 : 4 है| ar (triangle BPD): ar (triangle ABC) ज्ञात करें |
View SolutionIn triangle ABC ,P is a point on BC such that BP : PC = 1 : 2 and Q is the mid point of BP. then, ar(triangle ABQ) :ar (triangle ABC) is equal to: त्रिभुज ABC में, P, BC पर स्थित ऐसा बिंदु है कि BP : PC = 1 : 2 है और Q, BP का मध्य बिंदु है | तो ar(triangle ABQ) :ar (triangle ABC) का मान क्या होगा ?
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 3 : 4 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 3 : 4 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View Solution
