Doubtnut Promotions Sticky

किसी वैद्युत् द्विध्रुव के कारण अक्षीय स्थिति में किसी बिन्दु पर विधुत क्षेत्र की तीव्रता का व्यंजक ज्ञात कीजिए |

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

वैधुत द्विध्रुव-जब दो समान परिमाण के विपरीत प्रवृत्ति के आवेश एक-दूसरे के अत्यंत समीप रखे हों तो इस निकाय को वैधुत द्विध्रुव कहते हैं |
मानलो AB एक वैधुत द्विध्रुव है जो +q और -q आवेश से मिलकर बना है | मानलो दोनों आवेशों की बीच की दूरी 2l है | इस द्विध्रुव के मध्य बिन्दु O से अक्षीय स्थिति में r दूरी पर एक बिन्दु P है, जिस पर विधुत क्षेत्र की तीव्रता ज्ञात करनी है |
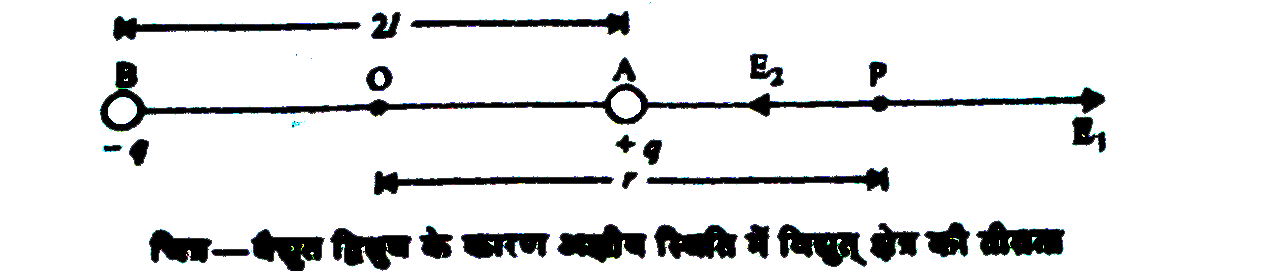
ocr_image
बिन्दु A पर स्थित +q आवेश के कारण बिन्दु P पर विधुत क्षेत्र की तीव्रता
E1=14πε0.qAP2
या E1=14πε0.q(r−l)2 (AP दिशा में)
इसी प्रकार बिन्दु B पर स्थित -q आवेश के कारण बिन्दु P पर विधुत क्षेत्र की तीव्रता
E2=14πε0.qBP2
या E2=14πε0.q(r+l)2 (PB दिशा में)
E1 और E2 एक ही रेखा में विपरीत दिशा में कार्यरत हैं तथा E1>E2
∴ बिन्दु P पर परिणामी तीव्रता
E=E1−E2(AP दिशा में)
या E=14πε0.q(r−l)2−14πε0.q(r+l)2
=q4πε0[1(r−l)2−1(r+l)2]
=q4πε0[(r+l)2−(r−l)2(r−l)2(r+l)2]
=q4πε0.4rl(r2−l2)2
=14πε0.2×q×2l×r(r2−l2)2
या E=14πε0.2pr(r2−l2)2, (∵ द्विध्रुव आघूर्ण p=q×2l)
इसकी दिशा AP के अनुदिश होगी |
यदि l<<r हो, तो
E=14πε0.2pr(r2)2=14πε0.2prr4
∴ E=14πε0.2pr3
इस स्थिति में क्षेत्र की दिशा -q से +q की ओर होती है |

|
Updated on:21/07/2023
Class 12PHYSICSELECTROSTATICS

Topper's Solved these Questions

Similar Questions