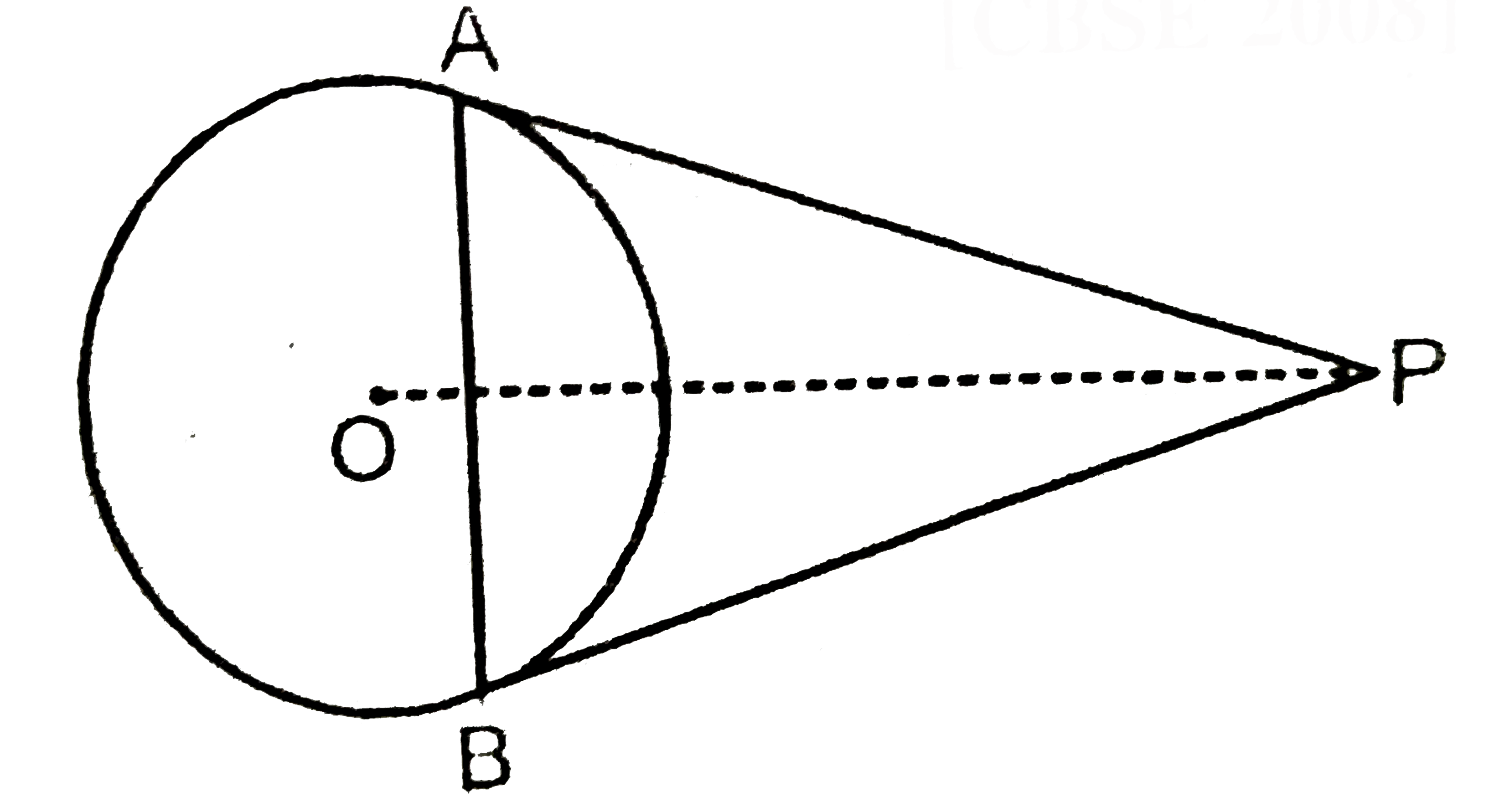
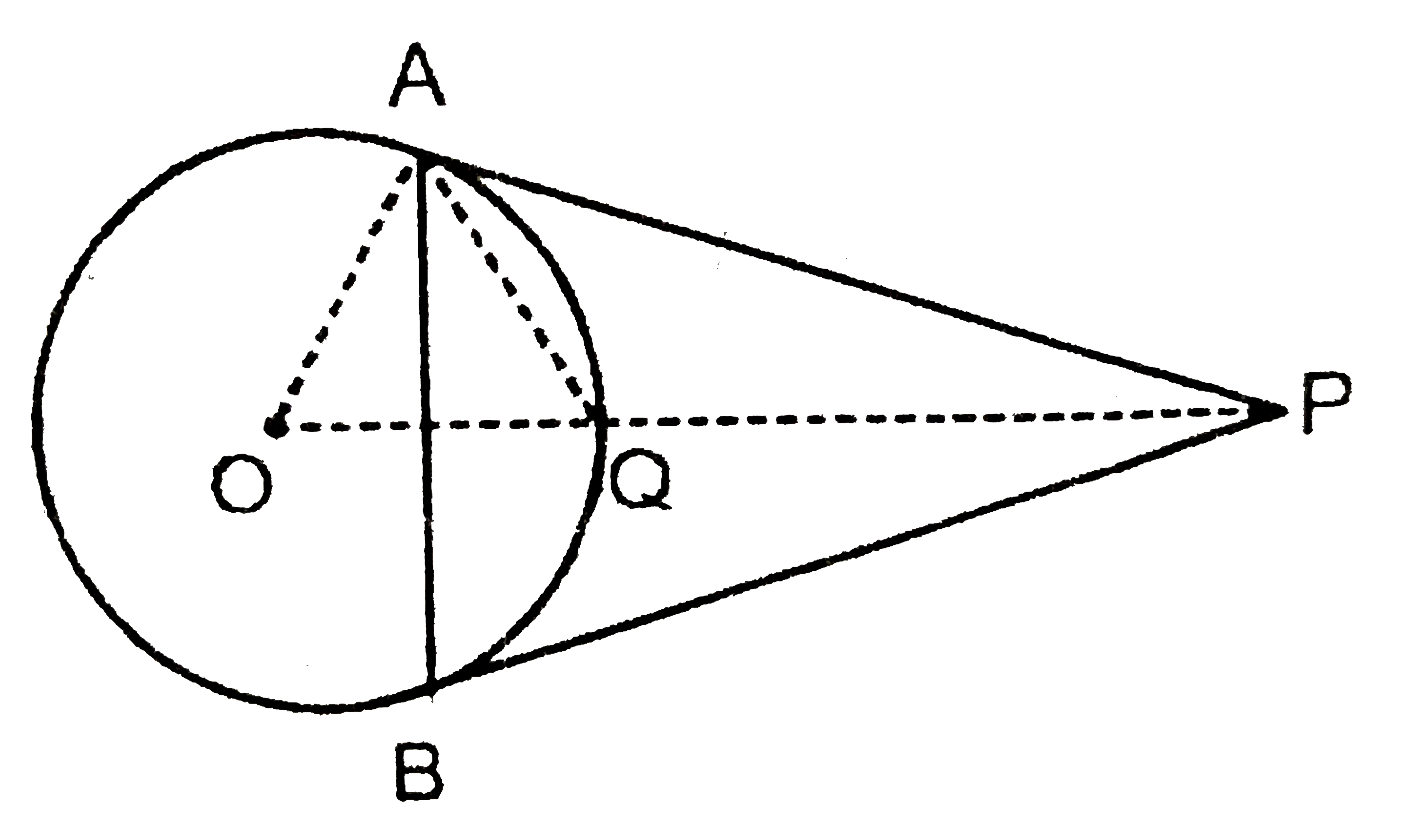
वृत्त (O,r) के बाहर बिंदु P से PAऔर PB दो स्पर्श रेखाएँ खींची गई हैं| दिखाएँ कि यदि OP=2r, तो △APB समबाहु त्रिभुज हैं|
मान लें कि OP वृत्त को Q पर काटती है|
OA और AQ को मिलाया|
∴OAQ=90∘
∴OP=OP−OQ=2r−r=r
अब OAP का समकोण त्रिभुज है, जिसका कोण A समकोण है और Q, OP का मध्य बिंदु है|
∴QA=OQ=QP=r
इस तरह OA = OQ = OA =r
∴△AOQ का समबाहु त्रिभुज है|
तब ∠AOQ=60∘⇒∠APO=30∘
⇒∠APB=2∠APO=60∘
अब PA = PB
⇒∠PAB=∠PBA=60∘
अब PA = PB
⇒∠PAB=∠PBA=60∘
इस प्रकार ∠PAB=∠PBA=∠APB=60∘
अतः △APB एक समबाहु त्रिभुज है|
Topper's Solved these Questions
- वृत्त BOOK - KC SINHACHAPTER - वृत्त EXERCISE - Exercise 10.1
15 Videos
- वृत्त BOOK - KC SINHACHAPTER - वृत्त EXERCISE - अतिलघु उत्तरीय प्रशन
32 Videos
- वास्तविक संख्याएं BOOK - KC SINHACHAPTER - वास्तविक संख्याएं EXERCISE - वस्तुनिष्ट प्रशन
28 Videos
- वृत्तों से संबंधित क्षेत्रफल BOOK - KC SINHACHAPTER - वृत्तों से संबंधित क्षेत्रफल EXERCISE - वस्तुनिष्ठ प्रश्न
21 Videos
Similar Questions
वृत्त के केंद्र से 5cm दूर स्थित बिंदु A से वृत्त पर खींची गई स्पर्श रेखा की लम्बाई 4cm हैं। वृत्त की त्रिज्या ज्ञात करें।
View Solutionएक बिंदु P से, वृत्त की स्पर्श रेखा की लम्बाई 15 सेमी. हैं और P की दुरी केंद्र से 17 सेमी. हैं,तो वृत्त की त्रिज्या क्या हैं?
View Solution(3−√3) है
View Solutionयदि एक अर्द्धवृत का परिमाप 36 cm हो, तो इसकी त्रिज्या है |
View Solutionयदि किसी बिंदु P के परवलय y2=4x पर खींची गई दो स्पर्श-रेखाएँ परस्पर लम्ब हों, तो P का बिन्दुपथ है :
View Solutionवृत्त के बाहर स्थित बिंदु से खींची गई स्पर्श रेखाओं की संख्या हो सकती है:
View Solutionएक 4 सेमी त्रिज्या के वृत्त पर बाह्य बिंदु से दो स्पर्श रेखाओ PA तथा PB कि रचना कीजिए। जहाँ PA तथा PB के मध्य कोण 65∘ है।
View SolutionPA and PB are tangents to a circle with centre O, from a point P outside the circle, and A and B are points on the circle. If angle APB= 40^@ , then angle OAB is equal to: PA तथा PB एक वृत्त के बाहर स्थित बिंदु P से वृत्त की स्पर्श रेखाएं हैं जिसका केंद्र O है तथा A और B वृत्त पर स्थित बिंदु हैं | यदि angle APB= 40^@ है, तो angle OAB का मान ज्ञात करें |
View SolutionPA and PB are two tangents to a circle with centre O from a point P outside the circle.A and B are points on the circle. If angle OAB =35^@ than angle APB is equal to: PA और PB केंद्र O वाले एक एक वृत्त की दो स्पश्रिखाएं हैं जो वृत्त के बाहर स्थित बिंदु P से निकली हैं |A और B वृत्त पर स्थित दो बिंदु हैं | यदि कोण angle OAB =35^@ है, तो कोण APB किसके बराबर होगा ?
View SolutionPA and PB are two tangents from a point P outside a circle with centre O. If A and B are points on the circle such that angle APB= 80^@ , then angle OAB is equal to: PA और PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली दो स्पर्श रेखाएं हैं | यदि A और B वृत्त पर स्थित ऐसे दो बिंदु हैं कि angle APB= 80^@ है, तो angle OAB का मान क्या होगा ?
View SolutionPA and PB are the tangents to a circle with centre O, from a point P outside the circle. A and B are the points on the circle. If angle APB= 72^@ ,then angle OAB is equal to: PA तथा PB एक वृत्त पर वृत्त के बाहर स्थित बिंदु P से खींची गयी स्पर्श रेखाएं हैं जिसका केंद्र O है | A तथा B वृत्त पर स्थित बिंदु हैं | यदि angle APB= 72^@ है, तो angle OAB का मान ज्ञात करें |
View SolutionPA and PB are two tangents from a point P outside the circle with centre O. If A and B are points on the circle such that ∠APB=110∘, then ∠OAB is equal to:
PA तथा PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली स्पर्श रेखाएं हैं | यदि A और B वृत्त पर स्थित ऐसे बिंदु हैं कि ∠APB=110∘ है, तो ∠OAB किसके बराबर है ?
View SolutionPA and PB are two tangents from a point P outside the circle with centre O. If A and B are points on the circle such that ∠APB=40∘, then ∠OAB is equal to:
PA तथा PB केंद्र O वाले वृत्त के बाहर स्थित बिंदु P से निकली दो स्पर्श रेखाएं हैं | A तथा B वृत्त पर स्थित बिंदु हैं |यदि ∠APB=40∘ है, तो ∠OAB किसके बराबर है ?
View SolutionFrom a point P outside the circle with centre O, two tangents PA and PB are drawn to meet the circle at A and B respectively. If ∠APB=70∘, then ∠OAB is equal to :
केंद्र O वाले वृत्त के बाहर स्थित किसी बिंदु P से दो स्पर्श रेखाएं PA और PB खींची जाती हैं जो वृत्त से क्रमशः A और B मिलती हैं | यदि ∠APB=70∘ है, तो कोण OAB का मान ज्ञात करें |
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠OAB=20∘, then ∠APB is equal to:
PA तथा PB केंद्र O वाले वृत के बाहर स्थित बिंदु P से वृत्त पर खींची गयी दो स्पर्श रेखाएं हैं | A और B वृत्त पर स्थित बिंदु हैं | यदि ∠OAB=20∘ है, तो ∠APB का मान कया होगा ?
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle A and B are points on the circle. If ∠APB=86∘, then ∠OAB is equal to:
PA तथा PB केंद्र O वाले वृत के बाहर स्थित बिंदु P से वृत्त पर खींची गयी दो स्पर्श रेखाएं हैं | A और B वृत्त पर स्थित बिंदु हैं | यदि ∠APB=86∘ है, तो ∠OAB का ज्ञात करें |
View Solution
