Question

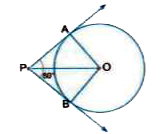
If PA and PB are tangents drawn from an external point P to a circle with centre O such that $\angle APB={70}^{\circ }$, then $\angle OAB$ is equal to:
यदि PA और PB एक बाहरी बिंदु P से केंद्र O के साथ एक वृत्त में खींची
गई स्पर्श रेखाएँ हैं जैसे कि $\angle APB={70}^{\circ }$ तो $\angle OAB$ बराबर है:

Options

A. a)`40^@`
B. b)`25^@`
C. c)`30^@`
D. d)`35^@`

Explanation

To solve the problem, we need to find the angle $$OAB$$ given that $$PA$$ and $$PB$$ are tangents from point $$P$$ to the circle with center $$O$$, and that $$\angle APB={70}^{\circ }$$.

1. Understanding the Geometry:
- We have a circle with center \( O \) and point \( P \) outside the circle.
- \( PA \) and \( PB \) are tangents to the circle at points \( A \) and \( B \) respectively.
- The angle \( \angle APB \) is given as \( 70^\circ \).

2. Using the Property of Tangents:
- The radius \( OA \) is perpendicular to the tangent \( PA \) at point \( A \). Therefore, \( \angle OAP = 90^\circ \).

3. Identifying Angles in Triangle OAP:
- In triangle \( OAP \), we have:
- \( \angle OAP = 90^\circ \)
- \( \angle APB = 70^\circ \)
- Let \( \angle OAB = x \).

4. Finding the Other Angle:
- In triangle \( OAP \), the sum of angles is \( 180^\circ \):
\( \angle OAP + \angle OAB + \angle BAP = 180^\circ \)
- Substituting the known values:
\( 90^\circ + x + (90^\circ - x) = 180^\circ \)
- Simplifying gives:
\( 180^\circ = 180^\circ \)
- This confirms our angles are consistent.

5. Using the Isosceles Triangle Property:
- Since \( PA = PB \) (both are tangents from point \( P \)), triangle \( PAB \) is isosceles.
- Therefore, \( \angle PAB = \angle PBA \).

6. Expressing Angles:
- Let \( \angle PAB = \angle PBA = 90^\circ - x \).

7. Applying the Angle Sum Property in Triangle PAB:
- The sum of angles in triangle \( PAB \) is:
\( \angle APB + \angle PAB + \angle PBA = 180^\circ \)
- Substituting the known values:
\( 70^\circ + (90^\circ - x) + (90^\circ - x) = 180^\circ \)
- This simplifies to:
\( 70^\circ + 180^\circ - 2x = 180^\circ \)
- Rearranging gives:
\( 70^\circ = 2x \)
- Therefore, solving for \( x \):
\( x = \frac{70^\circ}{2} = 35^\circ \)

8. Conclusion:
- Thus, the angle \( OAB \) is \( 35^\circ \).

Final Answer:
\( \angle OAB = 35^\circ \)