एक त्रिभुज ABC के आधार BC पर सम्मुख शीर्ष A से डाला गया लम्ब AD भुजा BC को D पर इस प्रकार काटता है की DB =3 CD है|सिद्ध करो की 2AB2=2AC2+BC2
दिया है की: DB=3CD
∴ BC=DB+DC
⇒ BC=3CD+CD
⇒ BC=4CD
⇒ CD=14BC और DB=3CD=34BC ...(i)
चूँकि ΔADB एक समकोण त्रिभुज है|अतः पाइथागोरस प्रमेय से
AB2=AD2+BD2 ....(ii)
इसी प्रकार समकोण ΔADC में पाइथागोरस प्रमेय से
AC2=AD2+DC2 ...(iii)
(ii ) में से (iii ) को घटाने से पर
AB2−AC2=BD2−CD2
⇒ AB2−AC2(34BC)2−(14BC)2 [(i)से BD=34BC,CD=14BC]
⇒ AB2−AC2=916BC2−116BC2
⇒ AB2−AC2=816BC2=12BC2
⇒ 2AB2−2AC2=BC2
⇒ 2AB2=2AC2+BC2
Topper's Solved these Questions
- त्रिभुजेंBook:RD SHARMAChapter:त्रिभुजेंExercise:प्रश्नावली 4.1
Explore 12 Videos
- त्रिभुजेंBook:RD SHARMAChapter:त्रिभुजेंExercise:प्रश्नावली 4.2
Explore 20 Videos
- त्रिकोणमितीय सर्वसमिकाएँ Book:RD SHARMAChapter:त्रिकोणमितीय सर्वसमिकाएँ Exercise:बहु विकल्पीय प्रश्न
Explore 28 Videos
- दो चार वाले रैखिक समीकरण युग्म Book:RD SHARMAChapter:दो चार वाले रैखिक समीकरण युग्म Exercise:बहु विकल्पीय प्रश्न
Explore 16 Videos
Similar Questions
कोष्ठक में दिए हुए शब्दों में से ही शब्दों को चुनकर रिक्त स्थान को भारिये:
सभी वृत.......(सर्वांगसम, समरूप) होते है|
View Solutionत्रिभुज ABC की भुजाओं AB और AC बिंदु D और E इस प्रकार है की DE भुजा BC के समानांतर है| यदि|||
AD=6 सेमि , DB = 9 सेमि तथा AE =8 सेमि, हो तो AC ज्ञात करो|
View Solutionयदि secθ+tanθ=x हो तो secθ=
View Solutionनिम्न समीकरण युग्म का अद्वितीय हल होंगे, यदि
kx−y=2
6x−2y=3
View SolutionThe perpendicular from A on side BC of a ABC intersects BC at D such that DB = 3 CD. Prove that 2AB^2 = 2AC^2 + BC^2.
View SolutionThe perpendicular AD on the base BC of a ABC intersects BC at D so that DB=3CD . Prove that 2 AB2=2 AC2+BC2 .
View SolutionIn Delta ABC seg AD perp seg BC,DB=3CD Prove that 2AB^(2)=2AC^(2)+BC^(2)
View SolutionIn the given figure, the of a ΔABC, interesects BC at D such DB=3CD. Prove that 2AB2=2AC2+BC2
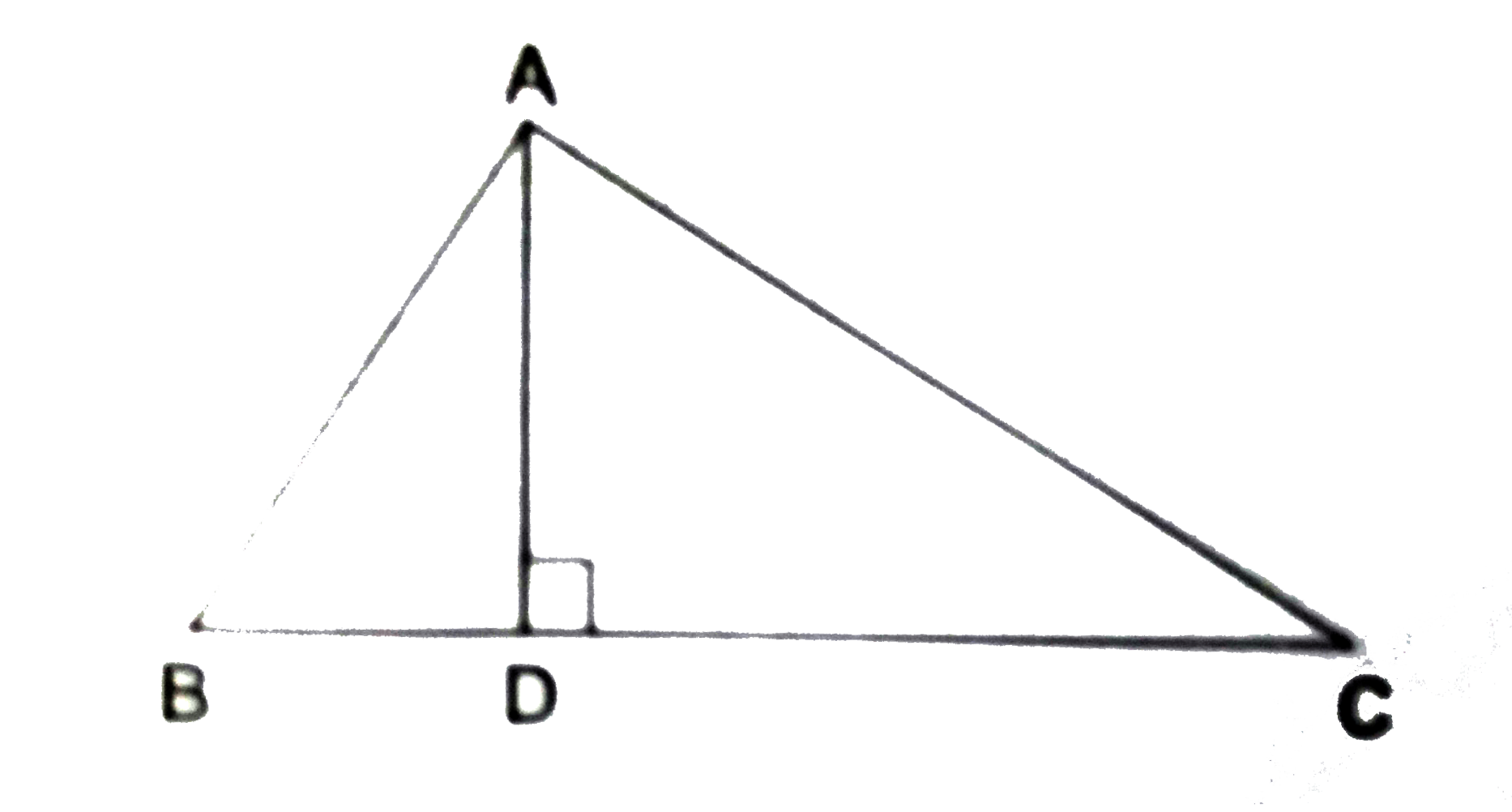
View SolutionIn ΔABC,AD⊥BC which intersects BC at D. If BD=3CD, then prove that 2AB2=2AC2+BC2
View SolutionΔABC के आधार BC पर डाला गया लंब AD भुजा BC को D पर प्रतिच्छेद करता है ।
यदि DB=3CD सिद्ध कीजिए कि 2AB2=2AC2+BC2.
View SolutionThe perpendicular from A on side BC at a ΔABC intersects BC at D such that DB=3 CD. Prove that 2AB2=2AC2+BC2
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View SolutionA யிலிருந்து வரையப்பட்ட செங்கோடு பக்கம் BC ஐ D யில் DB =3 CD என்னுமாறு ΔABC யில் வெட்டுகிறது 2AB2=2AC2+BC2 என நிரூபிக்க ?
View SolutionThe perpendicular from A on side BC of a ABC intersects BC at D such that DB = 3 CD. Prove that 2AB2=2AC2+BC2.
View SolutionIn ΔABC, seg AD⊥ seg BCDB=3CD.
Prove that : 2AB2=2AC2+BC2
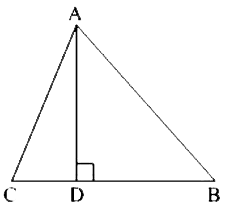
View Solution△ABC -এর BC বাহুর ওপর লম্ব AD এবং DB=3CD। প্রমাণ করো, 2AB2=2AC2+BC2
View Solution
