The perpendicular from A on side BC of a ABC intersects BC at D such that DB = 3 CD. Prove that .
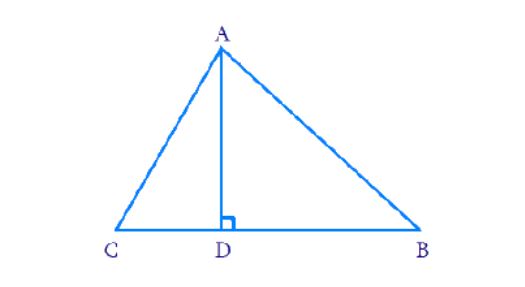
In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In , and
...... (1)
and, ..... (2)
In
[Using Pythagoras theorem]
In
[Using Pythagoras theorem ]
[from equation(3)]
[from equations(1) and (2)]
Thus,
Similar Questions
In Figure 3, AD⊥BC and BD=13CD. Prove that 2CA2=2AB2+BC2.
View SolutionIn Figure 2,AD⊥BC. Prove that AB2+CD2=BD2+AC2.
View SolutionIn an equilateral triangle ABC, D is a point on side BC such that BD=13BC. Prove that 9AD2=7AB2.
View SolutionIn the following figure, AD is perpendicular to BC and D divides BC in the ration 1 : 3.
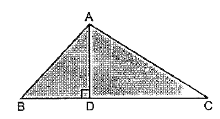
Prove that : 2AC2=2AB2+BC2
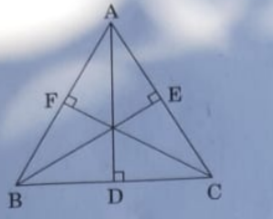
View SolutionIn Figure -6 , in an equilateral triangle ABC, AD is perpendicular to BC , BE is perpendicular to AC and CF is perpendicular to AB . Prove that 4(AD2+BE2+CF2)=9AB2
View SolutionIn Figure DE||BC and CD||EF. Prove that AD2=AB⋅AF.
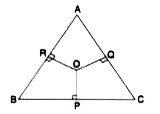
View SolutionIn the following figure, OP, OQ and OR are drawn perpendiculars to the sides BC, CA and AB repectively of triangle ABC. Prove that :
AR2+BP2+CQ2=AQ2+CP2+BR2
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
F is equidistant from AB and BC.
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionP and Q are the mid-points of the CA and CD respectively of a triangle ABC, right angled at C. Prove that: 4AQ2=4AC2+ BC2, 4BP2=4BC2+AC2, and 4(AQ2+ BP2)=5AB2.
View Solution
