यदि एक आयत ABCD के अंदर स्थित एक बिंदु O है तो सिद्ध कीजिए की:
OB2+OD2=OC2+OA2
आयत ABCD के अंदर एक बिंदु O स्थित है जिससे गुजरती हुई AB के समांतर रेखा भुजाओं AD और BC को क्रमशः E और F पर काटती है|
समकोण त्रिभुजों OEA और OFC में पाइथागोरस प्रमेय से
OA2=OE2+AE2 और OC2=OF2+CF2
इन दोनों को जोड़ने पर
⇒ OA2+OC2=OE2+AE2+OF2+CF2
⇒ OA2+OC2=OE2+OF2+AE2+CF2....(i)
समकोण त्रिभुज OFB O OED में पाइथागोरस प्रमेय से
OB2=OF2+FB2 तथा OD2=OE2+DE2
इन दोनों को जोड़ने पर
OB2+OD2=OF2+FB2+OE2+DE2
⇒ OB2+OD2=OE2+OF2+DE2+BF2
⇒ OB2+OD2=OE2+OF2+CF2+AE2 [∵DE=CF तथा AE =BF ]
⇒ OB2=OD2=(OE2+AE2)+(OF2+CF2) ...(ii)
(i ) व (ii ) से
OB2+OC2=OB2+OD2

Topper's Solved these Questions
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.1
12 Videos
- त्रिभुजेंBOOK - RD SHARMACHAPTER - त्रिभुजेंEXERCISE - प्रश्नावली 4.2
20 Videos
- त्रिकोणमितीय सर्वसमिकाएँ BOOK - RD SHARMACHAPTER - त्रिकोणमितीय सर्वसमिकाएँ EXERCISE - बहु विकल्पीय प्रश्न
28 Videos
- दो चार वाले रैखिक समीकरण युग्म BOOK - RD SHARMACHAPTER - दो चार वाले रैखिक समीकरण युग्म EXERCISE - बहु विकल्पीय प्रश्न
16 Videos
Similar Questions
कोष्ठक में दिए हुए शब्दों में से ही शब्दों को चुनकर रिक्त स्थान को भारिये:
सभी वृत.......(सर्वांगसम, समरूप) होते है|
View Solutionत्रिभुज ABC की भुजाओं AB और AC बिंदु D और E इस प्रकार है की DE भुजा BC के समानांतर है| यदि|||
AD=6 सेमि , DB = 9 सेमि तथा AE =8 सेमि, हो तो AC ज्ञात करो|
View Solutionयदि secθ+tanθ=x हो तो secθ=
View Solutionनिम्न समीकरण युग्म का अद्वितीय हल होंगे, यदि
kx−y=2
6x−2y=3
View Solutionआयत ABCD के अंदर स्थित O कोई बिंदु है सिद्ध कीजिए कि OB2+OD2=OA2+OC2 है

View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that OB=6cm,OD=8cmandOA=5cm, find the length of OC.
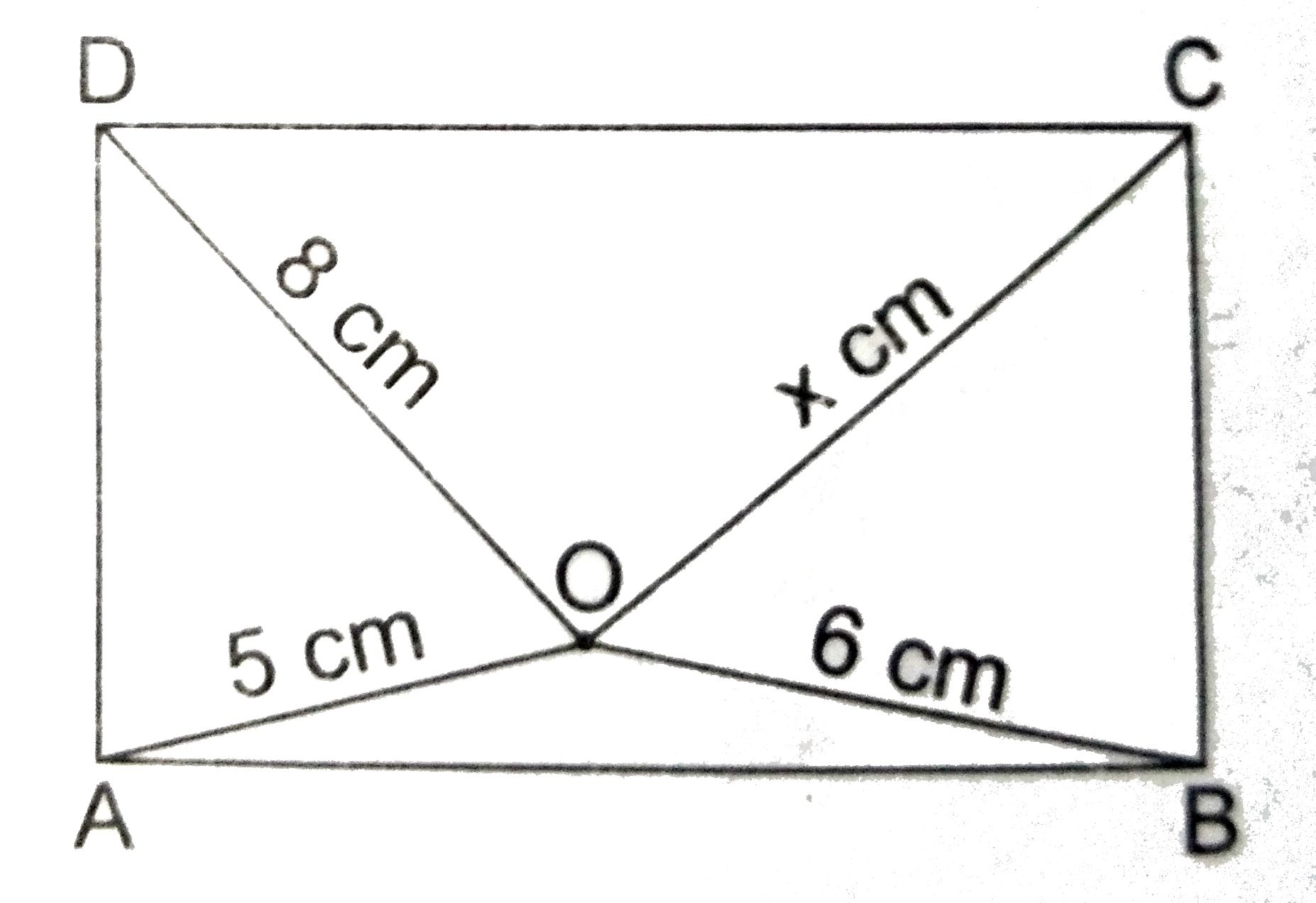
View Solutionआयतन ABCD के अंदर स्थित O कोई बिन्दु है । सिद्ध कीजिए कि OB2+OD2=OA2+OC2 है ।
View SolutionO is any point inside a rectangle ABCD, Prove that OA2+OC2=OB2+OD2
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View SolutionIn figure O is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
View SolutionO' is any point inside a rectangle ABCD.
Prove that OB2+OD2=OA2+OC2
View SolutionABCDE एक समपंचभुज है। O इसका केंद्र है। सिद्ध कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD+−−→OE=→0
View Solutionयदि ¯¯¯¯¯¯OA=¯a,¯¯¯¯¯¯OB=¯b तथा C,AB पर एक ऐसा बिंदु है कि ¯¯¯¯¯¯AC=3¯¯¯¯¯¯AB तो सदिश ¯¯¯¯¯¯OC बराबर है:
View Solutionएक आयत की भुजाओं की लम्बाईयाँ a और b है। यदि उसके एक शीर्ष को मुलबिन्दु तथा x- अक्ष को भुजा a के अनुदिश ले तो आयत की भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionएक 2.8 सेमी के वृत्त की रचना कर उस पर स्थित बिंदु P पर एक स्पर्श रेखा की रचना कीजिए।
View Solution
