O is any point inside a rectangle ABCD. Prove that $O B^{2} + O D^{2} = O A^{2} + O C^{2}$ .
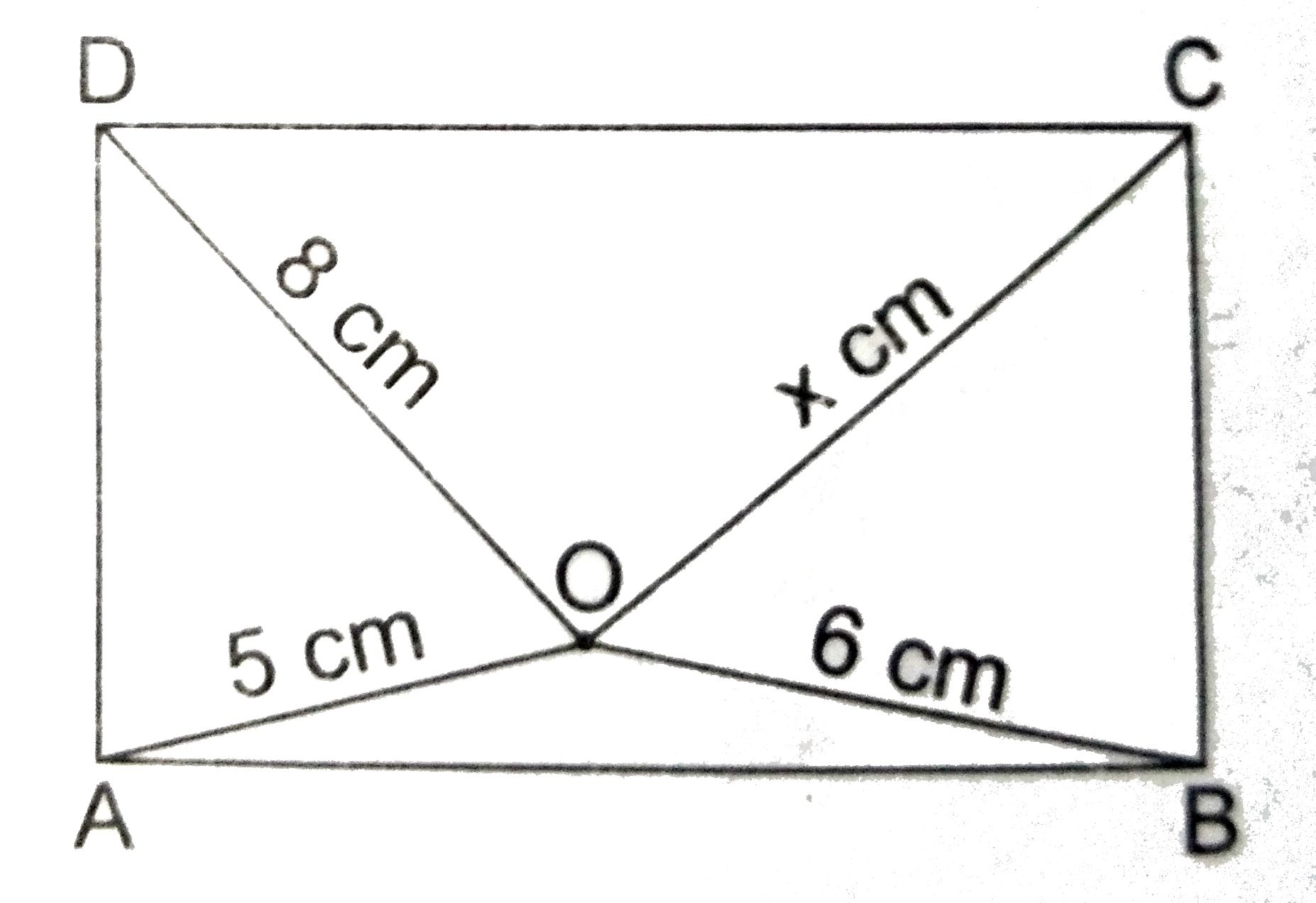
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that $O B = 6 c m, O D = 8 c m and O A = 5 c m,$ find the length of OC.

Video Solution

Text Solution

Verified by Experts

GIVEN O is point inside a rectangle ABCD.
TO PROVE $O B^{2} + O D^{2} = O A^{2} + O C^{2}$ .
CONSTRUCTION Through O, drawn $P O Q ∣ ∣ B C$ so that P lies on AB and Q lies on DC.

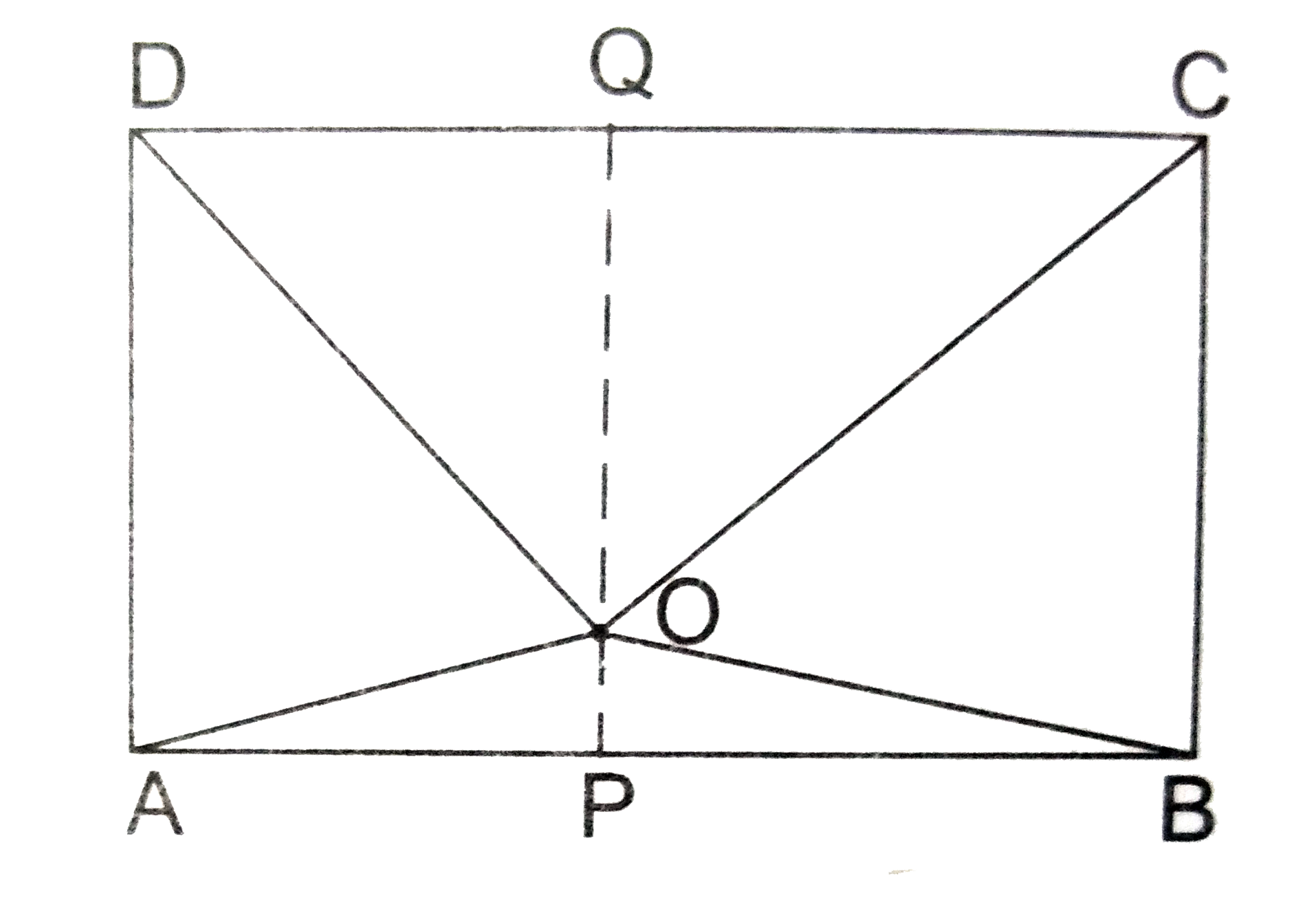
PROOF We have
$P O Q ∣ ∣ B C \Rightarrow P Q ⊥ A B and Q P ⊥ D C$
$\Rightarrow ∠ B P Q = 90^{\circ} and ∠ C Q P = 90^{\circ}$
$∴ B P = C Q$ [ oppositie sides of a rectangle]
$D Q = A P$ [ opposite sides of a rectangle]
From right $Δ O P B$ , we have $O D^{2} = O P^{2} + B P^{2}$
From right $Δ O Q D$ , we have $O D^{2} = O Q^{2} + D Q^{2}$
From right $Δ O P A$ , we have $O A^{2} = O P^{2} + A P^{2}$
From right $Δ O Q C$ , we have $O C^{2} = O Q^{2} + C Q^{2}$ .
$∴ O B^{2} + O D^{2} = O P^{2} + O Q^{2} + B P^{2} + D Q^{2} = O P^{2} + O Q^{2} + C Q^{2} + A P^{2} [∴ B P = C Q and D Q = A P]$
$= (O P^{2} + A P^{2}) + (O Q^{2} + C Q^{2})$
$= O A^{2} + O C^{2}$
Hence, $O B^{2} + O D^{2} = O A^{2} + O C^{2}$
DEFUCTION Let OC=xm
$O B^{2} + O D^{2} = O A^{2} + O C^{2}$
$\Rightarrow 6^{2} + 8^{2} = 5^{2} + x^{2}$
$\Rightarrow x^{2} = 36 + 64 - 25 = 75$
$\Rightarrow x = \sqrt{75} = 5 \sqrt{3} = (5 \times 1.732) = 8.66 \Rightarrow O C = 8.66$ cm

Updated on:21/07/2023

A point O lies inside a square ABCD such that OA=3, OB=4 and OD=5, find the value of OC.
AA) $\sqrt[3]{3}$
BB)6.67
CC) $\sqrt[3]{2}$
DD)4 $\sqrt[]{2}$
In the given figure, O is the centre of the circle. AB is tangent. $A B = 12 c m and O B = 13 c m$ . Find OA:

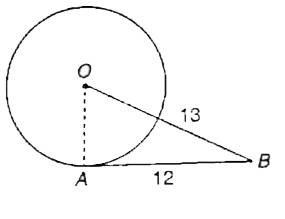A6.5 cm
B6 cm
C5 cm
Dnone of these
Diagonal $A C$ of a rectangle $A B C D$ is produced to the point $E$ such that $A C : C E = 2 : 1, A B = 8 c m$ and $B C = 6 c m$ . Find the length of $D E$ .
A $2 \sqrt{19}$ $c m$
B $15$ $c m$
C $3 \sqrt{17}$ $c m$
D $13$ $c m$