μ1 और μ2 अपवर्तनांक वाले (μ2>μ1) दो माध्यमों को पृथक करने वाले गोलीय उत्तर अपवर्तनांक पृष्ठ प्रकाश के अपवर्तन द्वारा बने वस्तु के प्रतिबिब निर्माण हेतु किरण आरेख इस आरेख की सहायता से निम्न सबंध की व्युत्पत्ति कीजिए ।
μ1v−μ1u=μ2−μ1R
जहाँ प्रयुक्त संकेतों के सामान्य अर्थ है ।
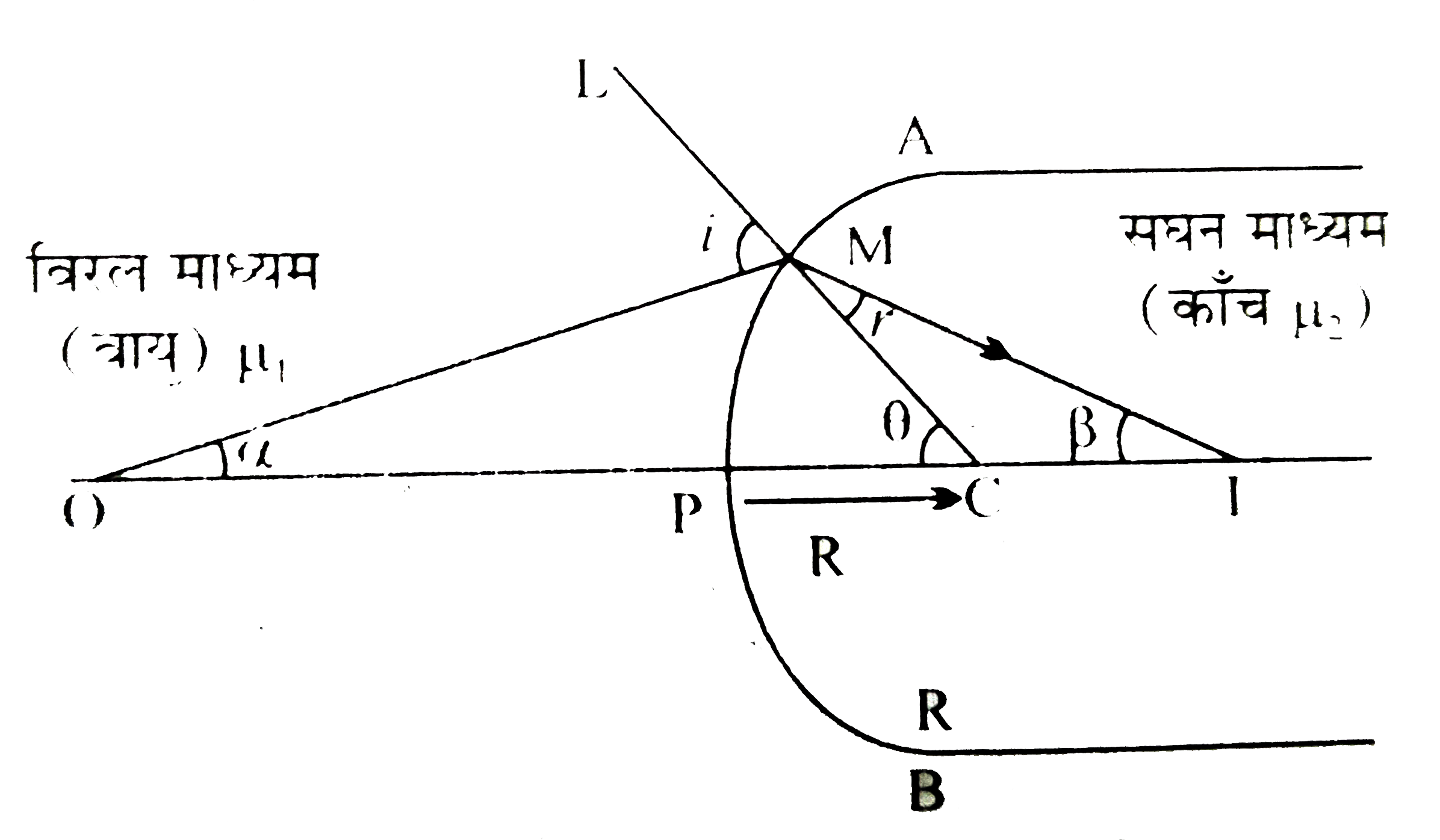
मान लो APB उत्तर पृष्ठ का मुख्य परिच्छेद है। इसके बायीं ओर वायु जिसका अपवर्तन μ1 तथा दाई ओर अपवर्तनांक μ2 का कोई माध्यम (काँच) है। P इसका ध्रुव तथा C वक्रता केंद्र है। इस पृष्ठ के मुख्य अक्ष पर बिंदु आकर की कोई वस्तु O स्थित है । θ से चलने वाली एक किरण OP वक्रता केंद्र C की दिशा में आपतित होती है । अतः बिना विचलित हुए सीधे चली जाती है । θ से चलने वाले दूसरी किरण OM अपवर्तन के पश्चात् अभिलंब CM की ओर मूड जाती है ओर MI मार्ग का अनुसरण करती है। दोनों किरणे परस्पर बिंदु I पर मिलती है । इस प्रकार θ का वास्तविक प्रतिबिंब I पर बनता है ।
आपतन कोण ∠OML=i
आपतन कोण ∠IMC=r
मान लो ∠MOC=α,∠MCP=θ
तथा ∠MIC=β स्नेल के नियमनुसार
μ=1β2=μ2μ1=sinisinr
μ1sini=μ2sin2 ...(1)
i ओर r के मान बहुत कम होते है अतः sini=i तथा sinr=r
μ2μ1=ir
μ1i=μ2r ..(2)
आपतित किरण, अपवर्तित किरण तथा अभिलंब मुख्या अक्ष के साथ क्रमशः α,β व θ कोण बनाते है।
तथा ΔOMg में i=α+θ
तथा ΔIMC में Q=r+β या r=θ−β
समीकरण (1) में, ओर i और r के मान रखने पर,
μ1(α+θ)=μ2(θ−β) ...(3)
सूत्र- कोण =चापत्रिज्या
Qα,β व θ के मान अंत्यंत अल्प है अतः
tanα=α=PMMO,tanβ=β,PMPI
तथा tanθ=θ=PMPC
पृष्ठ के बिंदु M के मुख्य अक्ष पर डाला गया लंब MP है। चूँकि P व P अत्यंत निकट है अतः PM=PM होंगे समी (3) में रखने पर,
μ1(PMPO+PMPC)=μ2(PMPC−PMPI)
μ1(1PO+1PC)=μ2(1PC−1PI)
PO=−u,PI=v,PC=+R
∴μ1(−1u+1R)=μ2(1R−1v)
μ2−μ1R=μ2v−μ1u
इस सूत्र को उत्तर पृष्ठ का अपवर्तन सूत्र कहते है।
Topper's Solved these Questions
- किरण प्रकाशिकी एवं प्रकाशीय यंत्र BOOK - PRABODH PUBLICATIONCHAPTER - किरण प्रकाशिकी एवं प्रकाशीय यंत्र EXERCISE - दीर्घ उत्तरीय प्रश्न
14 Videos
- किरण प्रकाशिकी एवं प्रकाशीय यंत्र BOOK - PRABODH PUBLICATIONCHAPTER - किरण प्रकाशिकी एवं प्रकाशीय यंत्र EXERCISE - आंकिक प्रश्न
12 Videos
- किरण प्रकाशिकी एवं प्रकाशीय यंत्र BOOK - PRABODH PUBLICATIONCHAPTER - किरण प्रकाशिकी एवं प्रकाशीय यंत्र EXERCISE - आंकिक प्रश्न
12 Videos
- किरण प्रकाशिकी एवं प्रकाशीय तंत्रBOOK - PRABODH PUBLICATIONCHAPTER - किरण प्रकाशिकी एवं प्रकाशीय तंत्रEXERCISE - मूल्य आधारित प्रश्न
9 Videos
- गतिमान आवेश ओर चुम्बकत्व BOOK - PRABODH PUBLICATIONCHAPTER - गतिमान आवेश ओर चुम्बकत्व EXERCISE - आंकिक प्रश्न
12 Videos
Similar Questions
प्रिज्म किसे कहते है ?
View Solutionएक मोमबत्ती को अवतल दर्पण के सम्मुख 4 सेमी की दुरी पर रखा गया है । दर्पण की वक्रता त्रिज्या 10 सेमी है। प्रतिबिम्ब की स्थिति, प्रकृति आवर्धन क्षमता परिकलित कीजिए।
View Solutionएक मोमबत्ती को अवतल दर्पण के सम्मुख 4 सेमी की दुरी पर रखा गया है । दर्पण की वक्रता त्रिज्या 10 सेमी है। प्रतिबिम्ब की स्थिति, प्रकृति आवर्धन क्षमता परिकलित कीजिए।
View Solutionशीला की नानी हमेशा सिर दर्द की शिकायत करती है। शीला उन्हें किसी नेत्र चिकित्सक को दिखाने के लिए कहती है लेकिन वे ये कहकर कि उनकी आँख ठीक है, मना कर देती है। उसकी नानी उसे सुई में धागा डालने के लिए भी कहती है। शीला उनकी समस्या समझ गई और नेत्र चिकित्सक के पास ले गई उन्होंने उन्हें चश्मा लगाने की सलाह दी।
शीला ने क्या निष्कर्ष निकाला ?
View Solutionतार की एक वृत्ताकार कुण्डली में 100 फेरे हैं । प्रत्येक की त्रिज्या 8.0 cm है ओर इनमें 0.40 A विद्युत धारा प्रवाहित हो रही है । कुण्डली हो रही है । कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र का परिणाम क्या होगा ?
View SolutionConsider the situation as shown in the figure. If mu_(1) is the friction coefficient between block A and incline and mu_(2) is the friction coefficient between block B and incline. Find the acceleration of block A if (a) mu_(1) = (1)/(5) , mu_(2) =(2)/(5) and (b) mu_(1) = (2)/(5) , mu_(2) = (1)/(5) .
View SolutionThe observer 'O' sees the distance AB as infinitely large. If refractive index of liquid is mu_(1) and that of glass is mu_(2) , then (mu_(1))/(mu_(2)) is : .
View Solution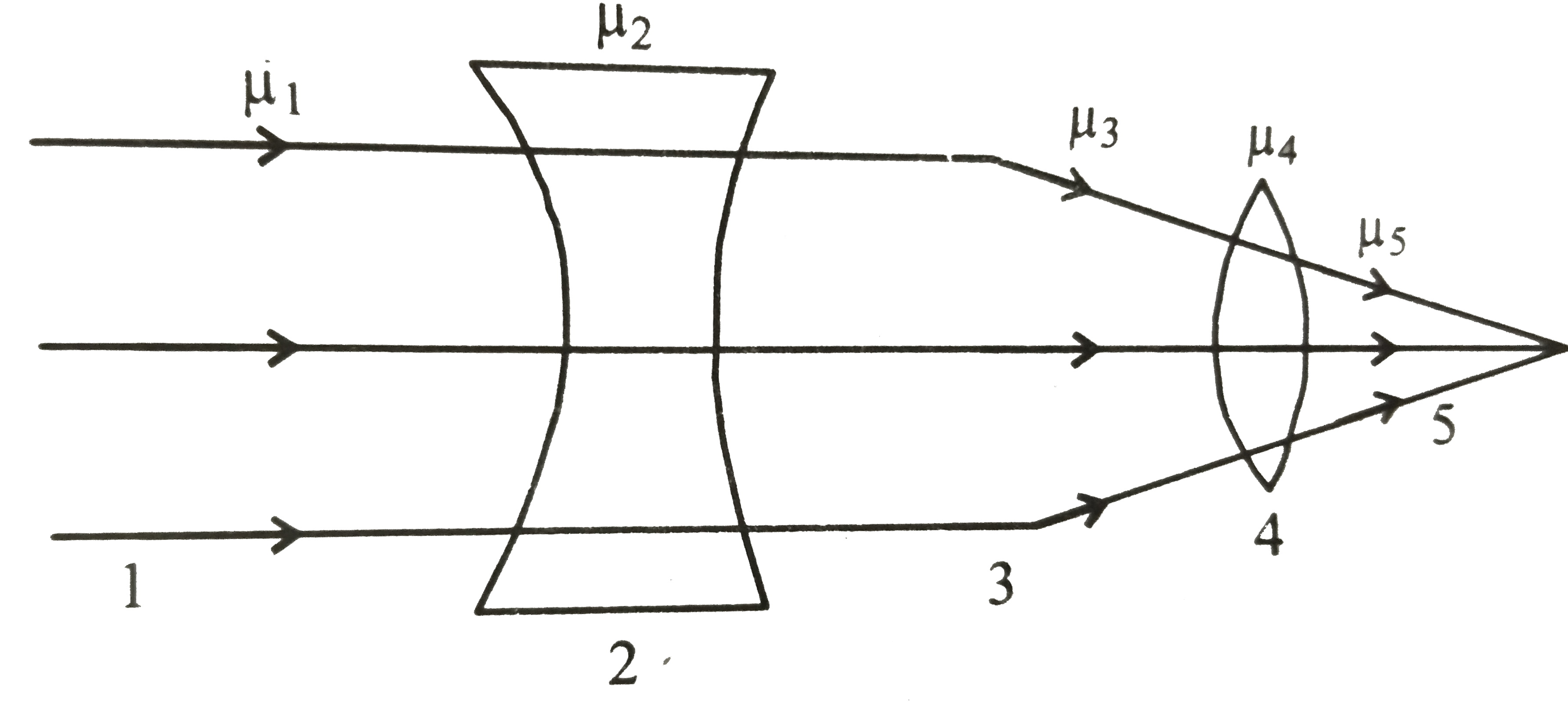
In the figure shown μ1,μ2,μ3,μ4andμ5 are the refractive
indices of the mediums 1,2,3,4 and 5 respectively. Consider
the following:
(1) μ1=μ2 (2) μ3=μ4=μ5
(3) μ2<μ3 (4) μ4>μ5
Which of the above are correct?
View Solutionकिसी गोलीय सतह से अपवर्तन के लिए सूत्र μ2v−μ1u=μ2−μ1r निकालें।
View Solutionसदिशों μ1=(1,2,3),μ2=(2,3,1),μ3=(1,3,2) और μ4=(4,6,2) के विषम में निम्नलिखित कथनो पर विचार कीजिये।
I.μ1,μ4 के समान्तर है II. μ2,μ4 के समान्तर है III.μ2,μ3 के समान्तर है
उपरोक्त कथनो में से कोण-सा/से कथन सही है/है?
View SolutionLight travels from a medium of refractive index μ1 to another of refractive index μ2(μ1>μ2). For total internal reflection of light, which is NOT true?
View SolutionThe reciprocalof ((mu_(2)-mu_(1))/(R)) gives the value of
View Solutionसिद्ध कीजिए कि 1μ2=12μ1.
View SolutionIf refractive index of core & cladding are μ1&μ2 respectively then :
View SolutionThe refractive indices of a medium for two light waves are μ1andμ2. If μ1>μ2, then which wave will move faster in the medium?
View SolutionThe refractive indices of three media 1,2 and 3 and mu_(1),mu_(2) and mu_(3) respectively (mu_(1) gt mu_(2) gt mu_(3)) . Which of the following statements are correct?
View Solution
