The observer 'O' sees the distance AB as infinitely large. If refractive index of liquid is μ1 and that of glass is μ2, then μ1μ2 is :
 .
.
2
1/2
4
none of these
The correct Answer is:A
Using formula of spherical surface taking 'B' as object
μ2∞−μ1(−2R)=μ2=μ1−R
(R being the radius of the curved surface)
μ2∞−μ1(−2R)=μ2−μ1−R⇒μ1μ2=2.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.109videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.1120videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.89videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
If refractive index of core & cladding are μ1 & μ2 respectively then :
Aμ1>μ2Bμ2>μ1Cμ1=μ2DNone of these - Question 2 - Select One
If refractive index of core & cladding are μ1&μ2 respectively then :
Aμ1>μ2Bμ2>μ1Cμ1=μ2DNone of these - Question 3 - Select One
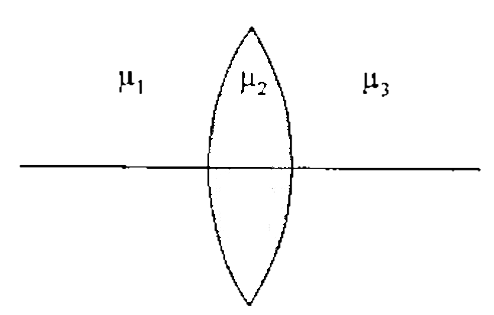
A double convex lens, lens made of a material of refractive index μ1, is placed inside two liquids or refractive indices μ2 and μ3, as shown. μ2>μ1>μ3. A wide, parallel beam of light is incident on the lens from the left. The lens will give rise to
 Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam
Aa single convergent beamBtwo different convergent beamsCtwo different divergent beamsDa convergent and a divergent beam
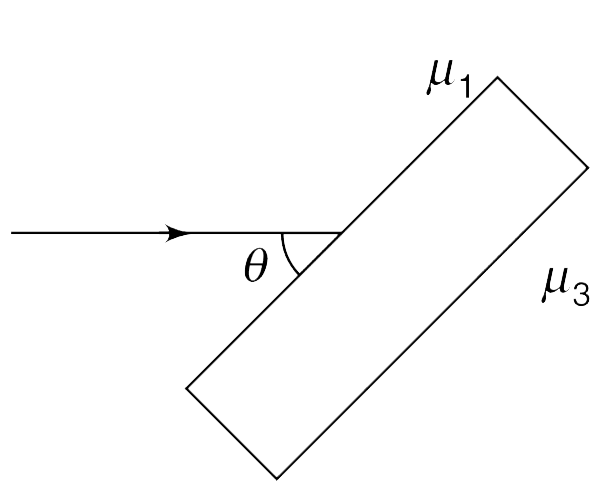
A light ray travelling in a medium of refractive index μ1 is incident on a parallel faced glass slab making an angle of θ with the glass surface. The refractive index of the medium on the other side of the glass slab is μ3(>μ1). Find the angular deviation suffered by the light ray.
 View Solution
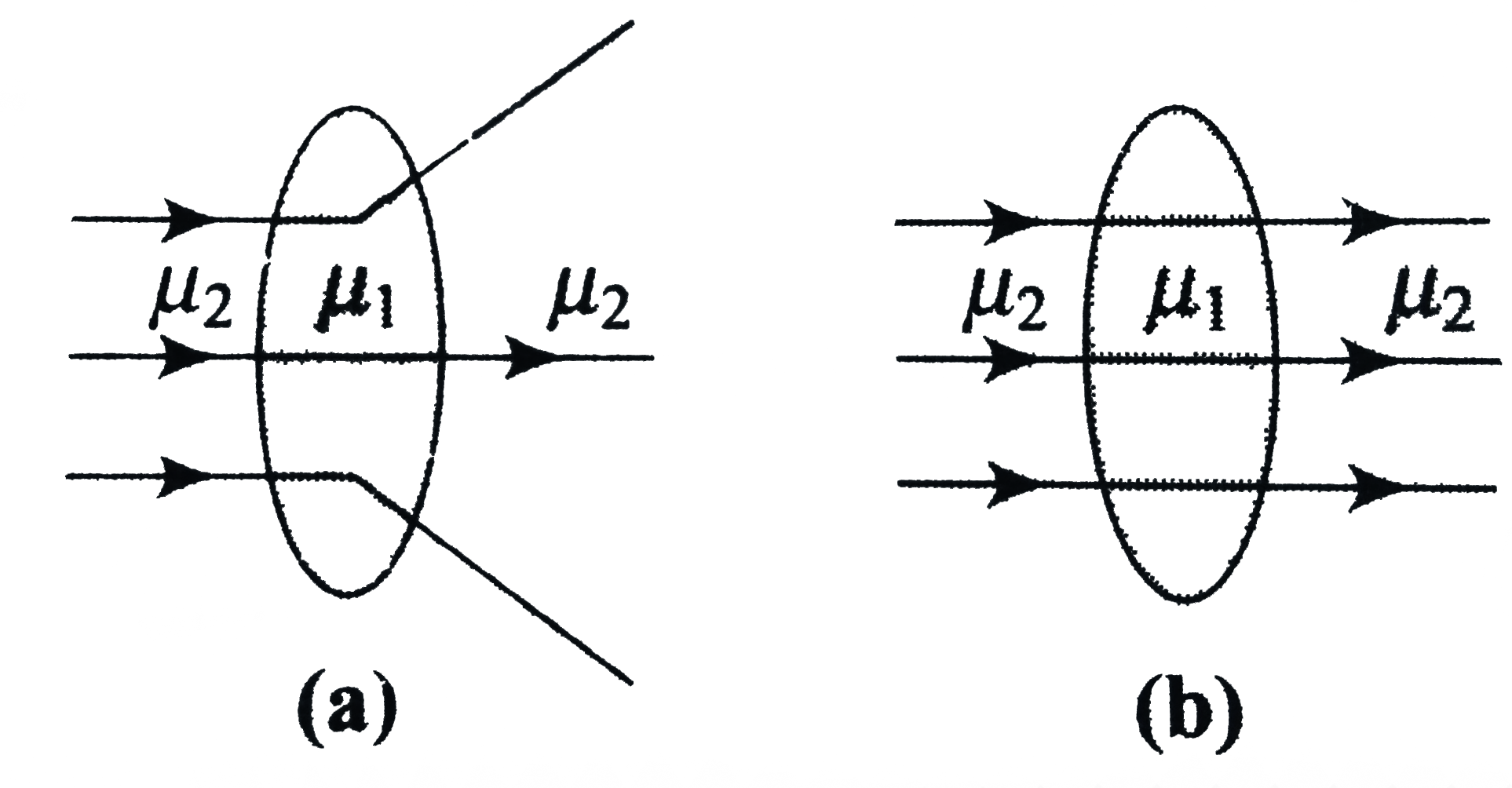
View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
 View Solution
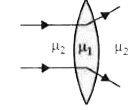
View SolutionA convex lens made up of material of refractive index μ1, is immersed in a medium of refractive index μ2 as shown in the figure. The relation between μ1 and μ2 is
 View Solution
View SolutionIf μ1andμ2are aboslute refractive index of medium 1 and medium 2 respectively, then
View SolutionIf a convex lens of refractive index μl is placed in a medium of refractive index μm Such that μl>μm>μair then
View Solution