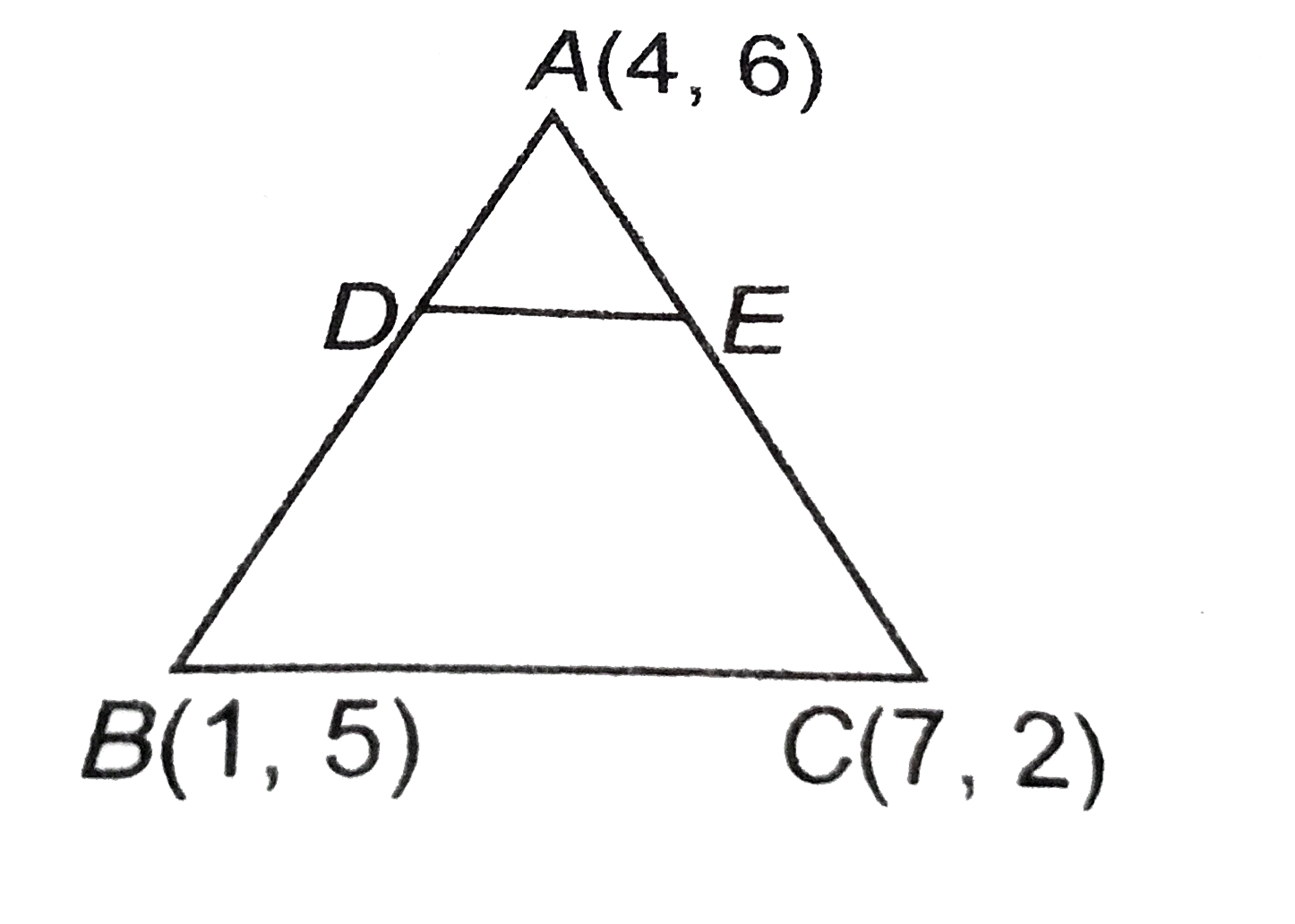
एक त्रिभुज ABC के शीर्ष A(4, 6), B(1, 5) और C(7, 2) हैं । भुजाओ AB और AC को क्रमश: D और E पर प्रतिच्छेद करते हुए एक रेखा इस प्रकार खींची गई है की ADAB=AEAC=14 है । ΔADE का क्षेत्रफल परिकलित कीजिए और इसकी तुलना ΔABC के क्षेत्रफल से कीजिए ।
∴ΔABC का क्षेत्रफल
=12[{4.5+1.2+7.6}−{1.6+7.5+4.2}]
=12[(20+2+42)−(6+35+8)]
=12(64−49)=152 वर्ग मात्रक
दिया है ADAB=13 ⇒ ADAD+BD=14
⇒ 4AD=AD+BD
⇒ 3AD=BD
⇒ ADBD=13=1:3
∴ बिंदु D, AB को 1 : 3 के अनुपात में विभाजित करता है । अत: बिंदु D के निर्देशांक
=(1x1+3×41+3=1×5+3×61+3)
=(1+124,5+184)=(134,234)
पुन: AEAC=14
⇒ AEAE+EC=14
⇒ 4AE=AE+EC
⇒ 3AE=EC
⇒ AEEC=13=1:3
∴ बिंदु E, AC को 1 : 3 के अनुपात में विभाजित करता है । अत: बिंदु E के निर्देशांक
=(1×7+3×41+3,1×2+3×61+3)
=(7+124,2+184)=(194,5)
अब A≡(4,6),D≡(134,234),E≡(194,5)
∴ΔADE का क्षेत्रफल ltbr=12[{4.234+134.5+194.6}−{134.6+194.234+4.5}]
=12[(23+654+1144)−(784+43716+20)]
=12[92+65+1144−312+437+32016]
=12[2714−106916]=12(1084−106916)
=1532 वर्ग मात्रक
अब ΔADE का क्षेत्रफलΔABC का क्षेत्रफल=15/3215/2=116=1:16
Topper's Solved these Questions
- निर्देशांक ज्यामितिBOOK - NOOTAN HINDICHAPTER - निर्देशांक ज्यामितिEXERCISE - अतिलघु उत्तरीय प्रश्न
10 Videos
- निर्देशांक ज्यामितिBOOK - NOOTAN HINDICHAPTER - निर्देशांक ज्यामितिEXERCISE - लघु उत्तरीय प्रश्न
10 Videos
- निर्देशांक ज्यामितिBOOK - NOOTAN HINDICHAPTER - निर्देशांक ज्यामितिEXERCISE - प्रश्नावली 7.3
5 Videos
- द्विघात समीकरण BOOK - NOOTAN HINDICHAPTER - द्विघात समीकरण EXERCISE - विविध प्रश्नावली (बहुविकल्पीय प्रश्न)
7 Videos
- पृष्ठीय क्षेत्रफल और आयतन BOOK - NOOTAN HINDICHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - बहुविकल्पीय प्रश्न
7 Videos
Similar Questions
a का मान ज्ञात कीजिए यदि बिंदु (3, a) रेखा 2x - 3y = 5 पर स्थित है ।
View Solutionयदि A(-2, 4) B(0, 0) और C(4, 2) ΔABC, के शीर्ष हैं, तो A से जाने वाली माध्यिका की लम्बाई ज्ञात कीजिए ।
View Solutionउस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष हैं :
(i) (2, 3), (-1, 0), (2, -4)
(ii) (-5, -1), (3, -5), (5, 2)
View Solutionनिम्नलिखित प्रश्न में चार विकल्प दिए गए हैं। उस विकल्प को चुनकर अपनी उत्तर पुस्तिका में लिखिए जिसके मूल वास्तविक हैं:
View Solutionएक सुराही निम्नलिखित का संयोजन है :
View SolutionIn triangle ABC, DE||BC where D is a point on AB and E is a point on AC. DE divides the area of triangle ABC into two equal parts.Then DB : AB is equal to एक त्रिभुज ABC DE||BC है जिसमें D,AB पर एक बिंदू है और E, AC पर एक बिंदू है। DE, triangle ABC के क्षेत्रफल को दो समान भागों में विभाजित करता है, DB : AB किसके बराबर हे?
View SolutionIn an isosceles triangle ABC with AB = AC and AD is perpendicular to BC, if AD = 6 cm and the perimeter of triangle ABC is 36 cm, then the area of triangle ABC is: एक समद्विबाह त्रिभुज ABC में AB=AC और AD, BC पर लंबवत है, यदि AD = 6 सेमी और ABC की परिधि 36 सेमी है, तो ABC का क्षेत्रफल है
View SolutionIn triangle ABC E and D are points on sides AB and AC,respectively, such that angle ABC= angle ADE , if AE = 6cm, AD = 4 cm and EB = 4 cm, then the length of DC is: triangle ABC में, E और D क्रमशः AB और AC पर एक बिंदु हैं, जैसे कि angle ABC= angle ADE ,यदि AE = 6cm, AD = 4 cm और EB = 4 cm है, तो DC की लंबाई है:
View SolutionIn an isosceles triangle ABC, AB=AC and AD is perpendicular to BC at D. If AD = 8 cm and perimeter of triangle ABC is 64cm, then the area of triangle ABC एक समद्विबाहु त्रिभुज ABC में, AB= AC और AD, BC पर लंबवत है। यदि AD =8 सेमी और ABC की परिधि 64 cm है, तो ABC का क्षेत्रफल है:
View SolutionIn a triangle ABC, AB =AC and the perimeter of A ABC is 8(2 + sqrt 2) cm . If the length of BC is sqrt 2 times the length of AB, then find the area of triangle ABC . एक त्रिभुज ABC में AB = AC और triangle ABC की परिधि 8(2 + sqrt 2) सेमी है। यदि 80 की लंबाई AB की लंबाई से sqrt 2 गुना है, तो triangle ABC का क्षेत्रफल ज्ञात कीजिए|
View SolutionThe area of a triangle ABC is one unit. DE is a straight line parallel to BC , joining the points D and E on AB and AC respectively such that AD : DB = 1 : 6. The ratio of the areas of the triangles ADE and ABC is : एक त्रिभुज ABC का क्षेत्रफल 1 इकाई है | DE, BC के समानांतर एक सीधी रेखा है जो क्रमशः AB और AC पर स्थित बिंदु D तथा E को इस प्रकार जोड़ती है कि AD : DB = 1 : 6 है | त्रिभुज ADE और ABC के क्षेत्रफल में अनुपात ज्ञात करें |
View SolutionIn a △ABC, D and E are two points on the sides AB and BC , respectively such that AD : DB = 2: 3 and DE || AC. If the area of △ADE is equal to 18 square cm, then what is the area ( In square cm) of △ABC ?
किसी त्रिभुज ABC में, D और E क्रमश: भुजा AB और BC पर स्थित बिंदु हैं जो इस प्रकार हैं कि AD : DB = 2: 3 है तथा 9DE || AC है | यदि त्रिभुज ADE का क्षेत्रफल 18 वर्ग सेमी के बराबर है, तो त्रिभुज ABC का क्षेत्रफल ( वर्ग सेमी में ) ज्ञात करें
View SolutionIn △ABC ,D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD /BD = 3/4 ,Then ratio of the area of trapezium DECB to the area of △ABC is:
त्रिभुज ABC में, D तथा E भुजा AB और AC पर स्थित ऐसे बिंदु हैं कि DE || BC और AD/BD = 3/4 है | समलम्ब DECB के क्षेत्रफल और त्रिभुज ABC के क्षेत्रफल में अनुपात ज्ञात करें ।
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =3/4 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =3/4 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल में अनुपात ज्ञात करें |
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE || BC and AD/BD =5/6 .The ratio of the area of △ABC to the area of trapezium DECB is :
त्रिभुज ABC में,D और E क्रमशः भुजा AB और AC पर स्थित ऐसे बिंदु है कि DE ||BC है और AD/BD =5/6 है | त्रिभुज ABC के क्षेत्रफल तथा समलम्ब DECB के क्षेत्रफल के बीच अनुपात ज्ञात करें |
View SolutionIn △ABC ,D and E are the points on sides AB and AC, respectively, such that DE || AC. If AD : DB = 5:3 then what is the ratio of the area of △BDE to that of the trapezium ACED ?/
त्रिभुज ABC में, D तथा E क्रमशः भुजा AB और BC पर स्थित ऐसे बिंदु हैं कि DE || AC है | यदि AD : DB = 5 : 3 है, तो त्रिभुज BDE के क्षेत्रफल और समलम्ब ACED के क्षेत्रफल में अनुपात ज्ञात करें |
View Solution
