In a triangle ABC, AB =AC and the perimeter of A ABC is 8(2+√2) cm . If the length of BC is √2 times the length of AB, then find the area of △ABC.
एक त्रिभुज ABC में AB = AC और △ABC की परिधि 8(2+√2) सेमी है। यदि 80 की लंबाई AB की लंबाई से √2 गुना है, तो △ABC का क्षेत्रफल ज्ञात कीजिए|
28cm2
36cm2
32cm2
16cm2
To find the area of triangle ABC, we will follow these steps:
Step 1: Understand the given information
We know that:
- Triangle ABC is isosceles with AB = AC.
- The perimeter of triangle ABC is 8(2+√2) cm.
- The length of side BC is √2 times the length of AB.
Let:
- AB=AC=x
- BC=y
From the information given, we can express the perimeter as:
AB+AC+BC=2x+y=8(2+√2)
Step 2: Express BC in terms of AB
From the problem, we have:
y=√2⋅x
Step 3: Substitute y in the perimeter equation
Substituting y in the perimeter equation:
2x+√2x=8(2+√2)
This simplifies to:
(2+√2)x=8(2+√2)
Step 4: Solve for x
Now, we can divide both sides by (2+√2):
x=8
Step 5: Find the length of BC
Now that we have x:
y=√2⋅x=√2⋅8=8√2
Step 6: Calculate the semi-perimeter (s)
The semi-perimeter s is given by:
s=AB+AC+BC2=2x+y2=2(8)+8√22=8+4√2
Step 7: Use Heron's formula to find the area
Heron's formula states:
Area=√s(s−a)(s−b)(s−c)
Where a=BC=8√2, b=AC=8, and c=AB=8.
Calculating s−a, s−b, and s−c:
- s−a=(8+4√2)−8√2=8−4√2
- s−b=(8+4√2)−8=4√2
- s−c=(8+4√2)−8=4√2
Now substituting these values into Heron's formula:
Area=√(8+4√2)(8−4√2)(4√2)(4√2)
Step 8: Simplify the expression
Calculating (8+4√2)(8−4√2):
=82−(4√2)2=64−32=32
Thus,
Area=√32⋅(4√2)⋅(4√2)=√32⋅32=√1024=32
Final Answer
The area of triangle ABC is 32cm2.
---
We know that:
- Triangle ABC is isosceles with AB = AC.
- The perimeter of triangle ABC is 8(2+√2) cm.
- The length of side BC is √2 times the length of AB.
- AB=AC=x
- BC=y
AB+AC+BC=2x+y=8(2+√2)
From the problem, we have:
y=√2⋅x
Substituting y in the perimeter equation:
2x+√2x=8(2+√2)
This simplifies to:
(2+√2)x=8(2+√2)
Now, we can divide both sides by (2+√2):
x=8
Now that we have x:
y=√2⋅x=√2⋅8=8√2
The semi-perimeter s is given by:
s=AB+AC+BC2=2x+y2=2(8)+8√22=8+4√2
Heron's formula states:
Area=√s(s−a)(s−b)(s−c)
Where a=BC=8√2, b=AC=8, and c=AB=8.
- s−a=(8+4√2)−8√2=8−4√2
- s−b=(8+4√2)−8=4√2
- s−c=(8+4√2)−8=4√2
Area=√(8+4√2)(8−4√2)(4√2)(4√2)
Calculating (8+4√2)(8−4√2):
=82−(4√2)2=64−32=32
Thus,
Area=√32⋅(4√2)⋅(4√2)=√32⋅32=√1024=32
The area of triangle ABC is 32cm2.
Topper's Solved these Questions
Similar Questions
In an isosceles triangle ABC, AB=AC and AD is perpendicular to BC at D. If AD = 8 cm and perimeter of △ABC is 64cm, then the area of △ABC
एक समद्विबाहु त्रिभुज ABC में, AB= AC और AD, BC पर लंबवत है। यदि AD =8 सेमी और ABC की परिधि 64 cm है, तो ABC का क्षेत्रफल है:
View SolutionIn an isosceles triangle ABC with AB = AC and AD is perpendicular to BC, if AD = 6 cm and the perimeter of △ABC is 36 cm, then the area of △ABC is:
एक समद्विबाह त्रिभुज ABC में AB=AC और AD, BC पर लंबवत है, यदि AD = 6 सेमी और ABC की परिधि 36 सेमी है, तो ABC का क्षेत्रफल है
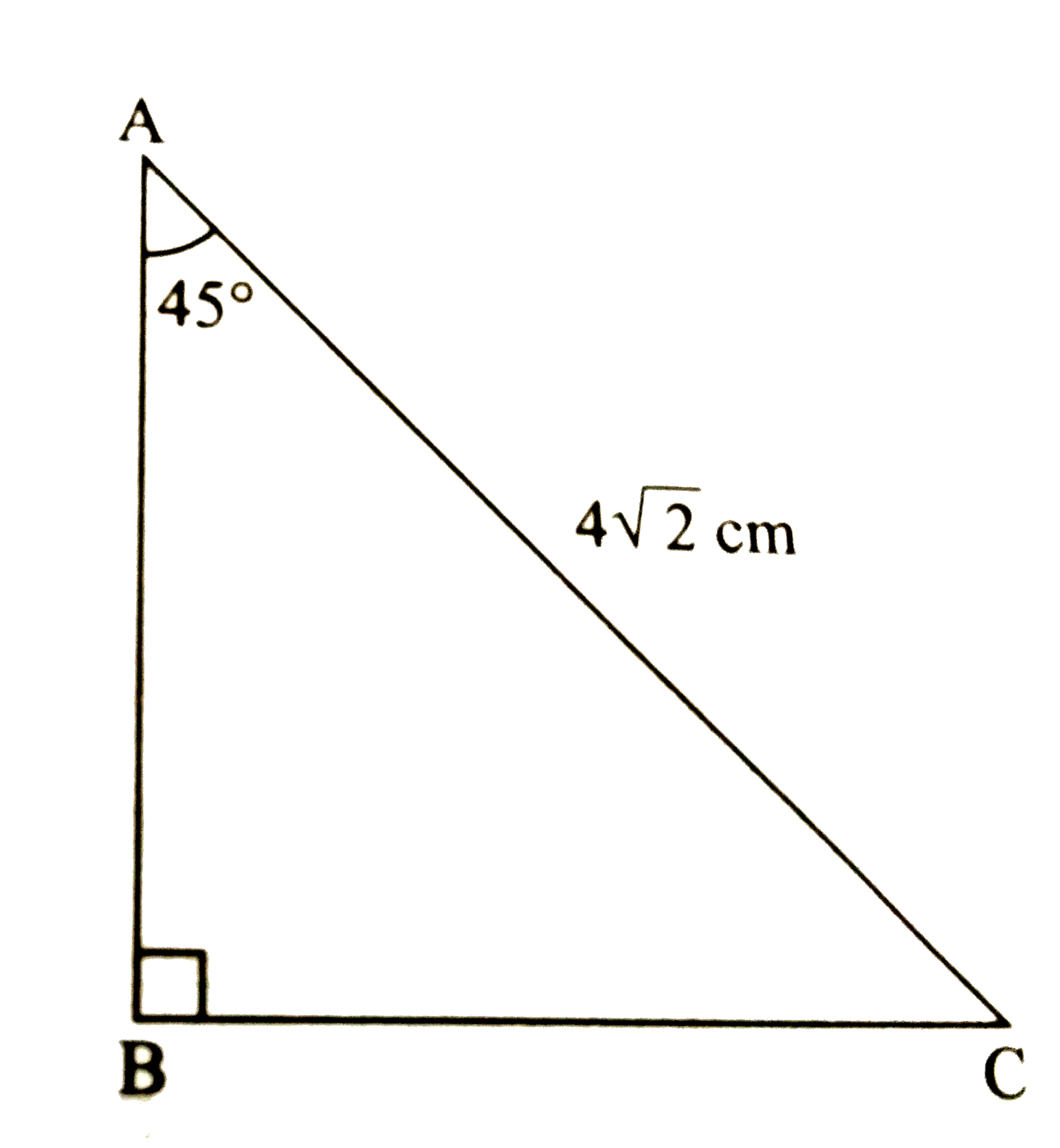
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
View SolutionIn ΔABC,AB=6cm,BC=7cm and AC=5cm .The area of ΔABC is
View SolutionIn △ABC ,AD is the bisector of ∠BAC, meeting BC at D. If AC= 21 cm, BC = 12 cm and the length BD is 2 cm less than DC, then the length of side AB is :
त्रिभुज ABC में, AD, ∠BAC का द्विभाजक है जो BC से D पर मिलता है| यदि AC =21 सेमी, BC =12 सेमी है और BD की लंबाईDC से 2 सेमी कम है, तो भुजा AB की लंबाई ज्ञात करें |
View SolutionFind the length of the altitude AL of an isoceles triangle ABC, where AB = AC = 5 cm and BC = 8 cm.
View SolutionIn triangle ABC, the length of BC is less than twice the length of AB by 2 cm. The length of AC exceeds the length of AB by 10 cm. The perimeter is 32 cm. The length (in cm) of the smallest side of the triangle is :
त्रिभुज ABC में, BC की लंबाई AB की लंबाई के दोगुने से 2 कम है | AC की लंबाई AB की लंबाई से 10 सेमी अधिक है | परिमाप 32 सेमी है | त्रिभुज की सबसे छोटी भुजा की लंबाई है -
View SolutionIn triangle ABC, the length of BC is less than twice the length of AB by 2 cm. The length of AC exceeds the length of AB by 10 cm. The perimeter is 32 cm. The length (in cm) of the smallest side of the triangle is :
त्रिभुज ABC में, BC की लंबाई AB की लंबाई के दोगुने से 2 कम है | AC की लंबाई AB की लंबाई से 10 सेमी अधिक है | परिमाप 32 सेमी है | त्रिभुज की सबसे छोटी भुजा की लंबाई है -
View SolutionIn a triangle ABC,∠B=90∘,D is the midpoint of AC,BD=√117. Sum of sides of AB & BC is 30 cm. Find the area of triangle ABC.
View SolutionIn a triangle ABC, the internal angle bisector of ∠ABC meets AC at K. If BC=2,CK=1andBK=3√22, then find the length of side AB.
View Solution
