4 सेमी त्रिज्या वाले एक वृत्त के परिगत एक त्रिभुज ABC इस प्रकार खींचा गया है कि रेखाखण्ड BD और DC ( जिसमे स्पर्श बिन्दु D द्रारा BC विभाजित है ) की लम्बाईयाँ क्रमशः 8 सेमी और 6 सेमी है (देखिए आकृति ) भुजाएँ AB और AC ज्ञात कीजिए।
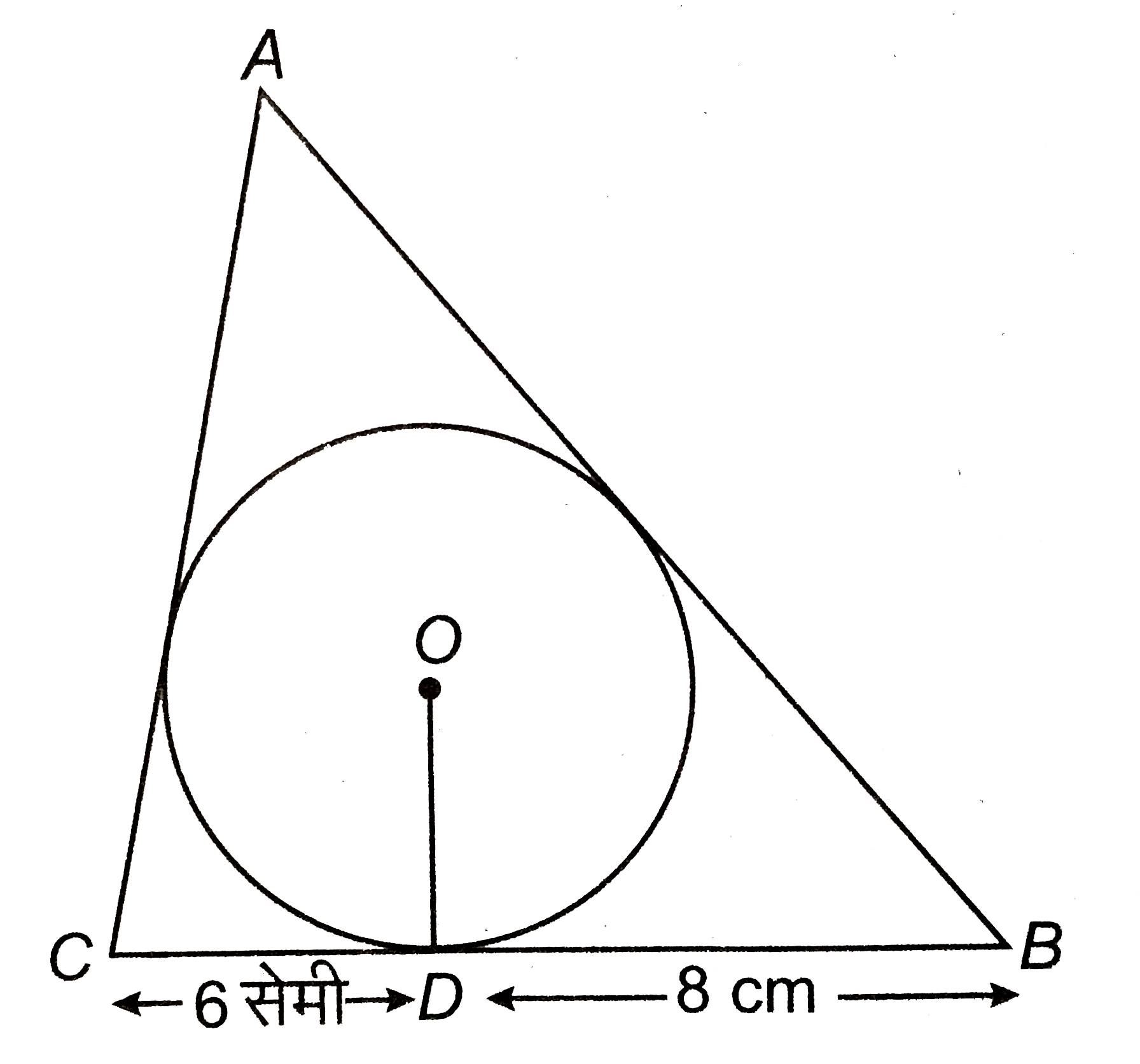
दिया है : CD = 6 सेमी, BD = 8 सेमी और त्रिज्या = 4 सेमी OC, OA और OB को मिलाया।
हम जानते है कि किसी बाह्य बिन्दु से वृत्त पर खींची स्पर्श रेखायें बराबर होती है।

∴CD=CF=6 सेमी
और BD=BE=8 सेमी
माना AF = AE = x सेमी
ΔOCB में,
त्रिभुज का क्षेत्रफल A1=12× आधार × ऊँचाई
=12×CB×OD
=12×14×4=28 सेमी2
ΔOCA में,
त्रिभुज का क्षेत्रफल A2=12×AC×OF
=12(6+x)×4=12+2x
ΔOBA में,
A3=12×AB×OE
=12(8+x)×4=16+2x
अब त्रिभुज ABC का अर्द्ध-परिमाप =12(AB+BC+CA)
s=12(x+6+14+8+x)=14+x
अब ΔABC का क्षेत्रफल =A1+A2+A3
=28+(12+2x)+(16+2x)
=56+4x ......(1)
हीरोन के सूत्र से,
ΔABC का क्षेत्रफल
=√s(s−a)(s−b)(s−c)
=√(14+x)(14+x−14)(14+x−x−6)(14+x−x−8)
=√(14+x)(x)(8)(6)=√(14+x)48x ....(2)
∴ समीकरण (1) और (2) से,
√(14+x)48x=56+4x
दोनों पक्षों का वर्ग करने पर,
(14+x)48x=42(14+x)2
⇒3x=4+x
⇒2x=14 ⇒x=7 lt brgt ∴AC=6+x=6+7=13 सेमी
AB=8+x=8+7=15 सेमी
Topper's Solved these Questions
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - विविध प्रश्नावली अतिलघु उत्तरीय प्रश्न
1 Videos
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - विविध प्रश्नावली
6 Videos
- वृत्त BOOK - NOOTAN HINDICHAPTER - वृत्त EXERCISE - प्रश्नावली 10.1
4 Videos
- वास्तविक संख्याएँBOOK - NOOTAN HINDICHAPTER - वास्तविक संख्याएँEXERCISE - विविध प्रश्नावली
30 Videos
- वृत्तों से समबन्धित क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - वृत्तों से समबन्धित क्षेत्रफल EXERCISE - विविध प्रश्नावली ( बहुविकल्पीय प्रश्न )
14 Videos
Similar Questions
7 सेमी त्रिज्या के वृत्त में, बिन्दु P से स्पर्श रेखा PT इस प्रकार खींची गई है कि PT = 24 सेमी है। यदि O वृत्त का केन्द्र है, तो OP की लम्बाई ज्ञात कीजिए।
View Solutionदी आकृति में, O केन्द्र के वृत्त में PT स्पर्श रेखा है। यदि OT = 6 सेमी और OP =10 सेमी है, तो स्पर्श रेखा PT की लम्बाई ज्ञात कीजिए।
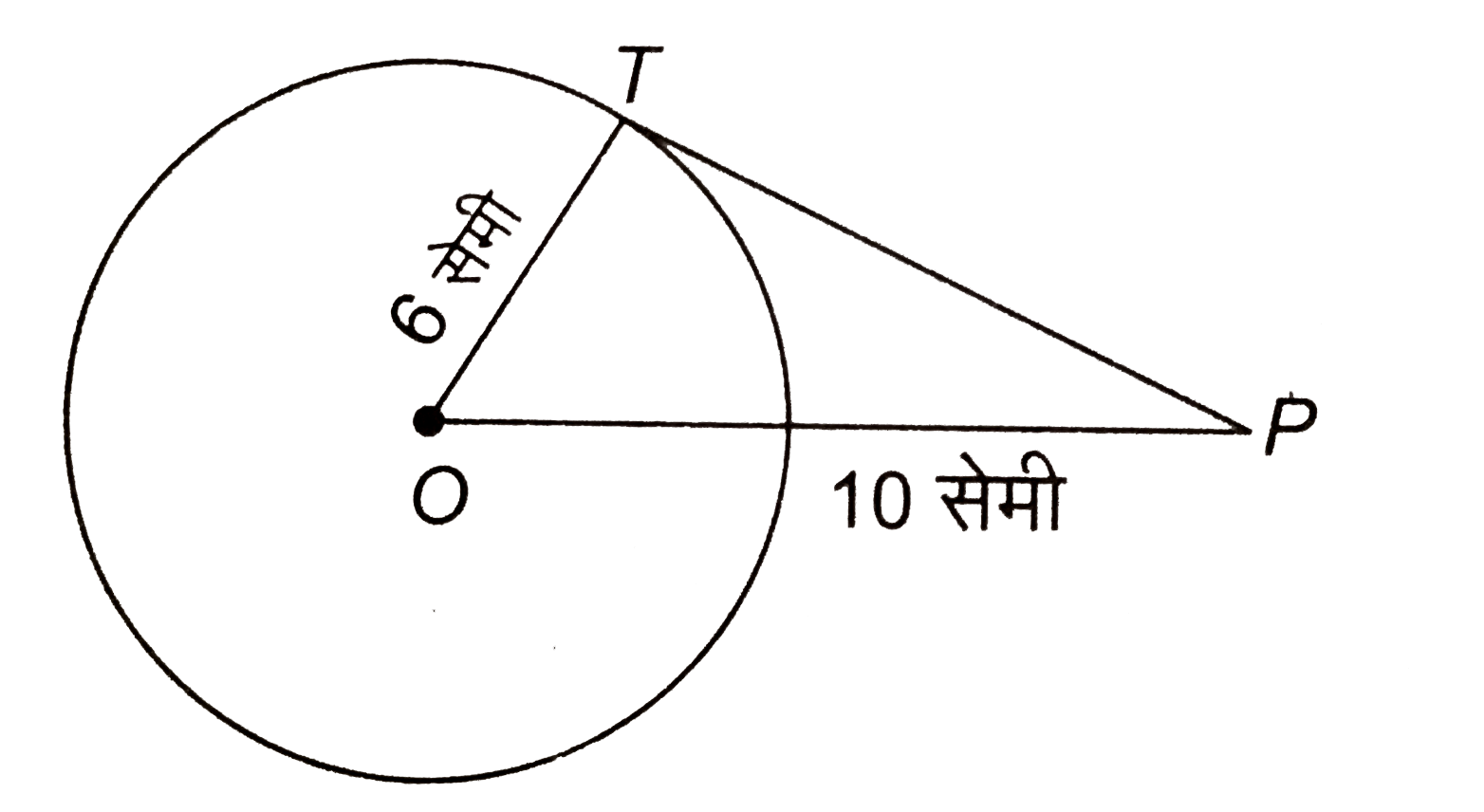
View Solutionएक वृत्त की कितनी स्पर्श रेखाएँ हो सकती है?
View Solutionयूक्लिड विभाजन प्रमेयिका बताइए।
View Solutionयदि R1 और R2 त्रिज्याओं वाले दो वृत्तों की परिधियों का योग R त्रिज्या के वृत्त की परिधि के बराबर है , तो :
View Solutionएक त्रिभुज ABC में मध्यिकाएँ AD ,BE और CF एक बिंदु G से गुजरती है। यदि AD=9 सेमी ,GE=4.2 सेमी और GC=6 सेमी ,तो AG , BE औरFG की लम्बाइयों के मान ज्ञात कीजिए।
View Solutionआकृति में PQ तथा RS एक वृत्त पर क्रमशः बिन्दु A और C पर स्पर्श रेखाएं है। यदि ∠ABC=60∘ और ∠BAP=40∘ हो तो ∠BCR ज्ञात कीजिए।

View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है, की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionदो वृत्त जिनकी त्रिज्याएँ क्रमशः 2.5 सेमी एवं 1.5 सेमी है जिनके केंद्र 8 सेमी दूरी पर स्थित है ,पर एक उभयनिष्ठ तिर्यक स्पर्श रेखा किन रचना कीजिए।
View Solutionदो वृत्तों, जिनकी त्रिज्याएँ क्रमशः सेमी 1.7 और 2.8 सेमी की है ,की एक उभयनिष्ठ तिर्यक स्पर्श रेखा की रचना कीजिए जबकि दोनों के केंद्र एक दूसरे से 6 सेमी दूरी पर है।
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View SolutionIn a circle centred at O, AB is a chord and C is any point on AB, such that OC is perpendicular to AB. If the length of the chord is 16 cm and OC = 6 cm, the radius of circle is : O केंद्र वाले एक वृत्त में, AB एक जीवा है और C, AB पर कोई बिंदु है, जैसे OC, AB पर लंबवत है। यदि जीवा की लंबाई 16 सेमी और OC = 6 सेमी है, तो वृत्त की त्रिज्या है:
View SolutionA circle is inscribed in a triangle ABC. It touches the sides AB, BC and AC at the points R, P and Q respectively. If AQ = 4.5 cm, PC = 5.5 cm and BR = 6 cm, then the perimeter of the triangle ABC is: एक वृत्त किसी त्रिभुज ABC में अन्तर्निहित है | यह भुजाओं AB, BC और AC को क्रमशः बिंदु R, P और Q पर स्पर्श करता है | यदि AQ = 4.5 सेमी, PC = 5.5 सेमी और BR = 6 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |
View SolutionIn triangle ABC , angle A is a right angle. The lengths of AC and BC 6 cm and 10 cm respectively. Point D is on AB such that BD = 4 cm. What is the length of CD? त्रिभुज ABC में, कोण A समकोण है | AC और BC की लंबाई क्रमशः 6 सेमी और 10 सेमी है | बिंदु D, AB पर इस प्रकार स्थित है कि BD = 4 सेमी है | CD की लंबाई ज्ञात करें |
View Solutiontriangle ABC is a triangle, where angle B is obtuse. AD is perpendicular on CB produced at D. If AB = 8cm, BC = 7cm and BD = 4cm, then AC is equal to : ABC एक त्रिभुज है, जिसमें कोण B अधिक कोण है | AD, CB पर लम्ब है जिसे D पर डाला गया है | यदि AB =8 सेमी, BC = 7 सेमी और BD = 4 सेमी है, तो AC किसके बराबर है ?
View Solution
