In a circle centred at O, AB is a chord and C is any point on AB, such that OC is perpendicular to AB. If the length of the chord is 16 cm and OC = 6 cm, the radius of circle is :
O केंद्र वाले एक वृत्त में, AB एक जीवा है और C, AB पर कोई बिंदु है, जैसे OC, AB पर लंबवत है। यदि जीवा की लंबाई 16 सेमी और OC = 6 सेमी है, तो वृत्त की त्रिज्या है:
10 cm
8 cm
6 cm
12 cm
To find the radius of the circle given the chord AB and the perpendicular distance OC, we can follow these steps:
1. Identify the Length of the Chord:
The length of the chord AB is given as 16 cm.
2. Determine the Half-Length of the Chord:
Since OC is perpendicular to AB, it bisects the chord into two equal parts. Therefore, the length of AC (or BC) is:
AC=AB2=16 cm2=8 cm
3. Identify the Length of OC:
The distance OC is given as 6 cm.
4. Form a Right Triangle:
In triangle OAC, we have:
- OC = 6 cm (perpendicular from the center to the chord)
- AC = 8 cm (half of the chord)
- OA = radius of the circle (which we need to find)
5. Use the Pythagorean Theorem:
According to the Pythagorean theorem:
OA2=OC2+AC2
Substituting the known values:
OA2=62+82
OA2=36+64
OA2=100
6. Calculate the Radius:
Taking the square root of both sides gives:
OA=√100=10 cm
Conclusion:
The radius of the circle is 10 cm.
The length of the chord AB is given as 16 cm.
Since OC is perpendicular to AB, it bisects the chord into two equal parts. Therefore, the length of AC (or BC) is:
AC=AB2=16 cm2=8 cm
The distance OC is given as 6 cm.
In triangle OAC, we have:
- OC = 6 cm (perpendicular from the center to the chord)
- AC = 8 cm (half of the chord)
- OA = radius of the circle (which we need to find)
According to the Pythagorean theorem:
OA2=OC2+AC2
Substituting the known values:
OA2=62+82
OA2=36+64
OA2=100
Taking the square root of both sides gives:
OA=√100=10 cm
The radius of the circle is 10 cm.
Topper's Solved these Questions
Similar Questions
In a circle centred at O, AB is a chord and C is any point on AB, such that OC is perpendicular to AB. If the length of the chord is 16 cm and OC = 6 cm, the radius of circle is :
O क वाले एक वृत्त में, AB एक जीवा है और C, AB पर कोई बिंदु है, जैसे OC, AB पर लंबवत है। यदि जीवा की लंबाई 16 सेमी और OC = 6 सेमी है, तो वृत्त की त्रिज्या है:
View SolutionIn a circle centred at O, AB is a chord and C is any point on AB such that OC is perpendicular to AB. If the radius of the circle is 10 cm and OC = 6 cm, then the length of the chord is:
एक वृत्त में O केंद्र है , AB एक जीवा है और C, AB पर कोई बिंदु है जैसे OC, AB पर लंबवत है। यदि वृत्त की त्रिज्या 10 सेमी और OC = 6 सेमी है, तो जीवा की लंबाई ज्ञात करे |
View Solution
Knowledge Check
In a circle with centre at O (0,0) 2. and radius 5 cm, AB is a chord of length 8 cm. If OM is perpendicular to AB, then the length of OM is:
A2.5cm.B3cm.C4cm.D1cm.O is the centre of a circle. AB is a chord of the circle but not its diameter. OC is perpendicular to AB. If OC = CB and radius of the circle be 7 cm, then the length of AB is
A7√2cmB14cmC7 cmD7√2 cm
In a circle with centre O, AD is a diameter and AC is a chord. Point B on AC such that OB = 7cm and ∠OBA=60∘. If ∠DOC=60∘, then what is the length of BC?
केंद्र वाले एक वृत्त में, AD एक व्यास है और AC एक जीवा है। AC पर एक बिंदु B इस प्रकार है की OB = 7 सेमी और ∠OBA=60∘ | यदि ∠DOC=60∘ है, तो BC की लंबाई क्या है?
View SolutionIn a circle two equal and parallel chords are 6 cm apart and lie on the opposite sides of the centre of the circle.If the length of each chord is 8 cm, than the radius of the circle is:
एक वृत्त में दो बराबर और समान्तर जीवाएँ 6 cm के दुरी पर हैं और वृत्त के केंद्र के विपरीत भाग पर स्थित हैं। यदि प्रत्येक जीवाएँ की लंबाई 8 सेमी है, तो वृत्त की त्रिज्या है:
View SolutionIn a circle of radius 5 cm, AB and AC are two chords such that AB=AC=6cm. Find the length of the chord BC
View SolutionIn a circle, AB is the diameter and CD is a chord. AB and CD produced meet at a point P, outside the circle. If PD = 15.3 cm, CD = 11.9 cm and AP = 30.6 cm, then the radius of the circle is:
एक वृत्त में, AB व्यास है तथा CD एक जीवा है | AB तथा CD को बढ़ाया जाता है जो वृत्त से बाहर एक बिंदु P पर मिलती हैं | यदि PD = 15.3 सेमी, CD = 11.9 सेमी तथा AP = 30.6 सेमी है, तो वृत्त की त्रिज्या कितनी है ?
View Solution.In given figure OC is perpendicular segment drawn from centre O to chord AB. If OB=5 cm and OC= 3cm then find the length of AB
View SolutionIn the given figure, TB is a chord which passes through the centre of the circle. PT is a tangent to the circle at the point. T on the circle. If PT = 10 cm, PA = 5 cm and AB = x cm, then the radius of the circle is:
दिए गए चित्र में, TB एक जीवा है जो वृत्त के केंद्र से होकर गुजरता है। PT, वृत्त के बिंदु T पर वृत्त की स्पर्शरेखा है। यदि PT= 10 सेमी, PA=5 सेमी और AB = x सेमी, तो वृत्त का त्रिज्या है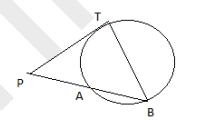
View Solution
