शंकु के एक छिन्नक के लिए , पूर्व स्पष्ट किए संकेतों का प्रयोग करते हूए , वक्र पृष्ठीय क्षेत्रफल और संपूर्ण पृष्ठीय क्षेत्रफल के उन सूत्रों को सिद्ध कीजिए , जो अनुच्छेद $13.5$ में दिए गए है ।

Video Solution

Text Solution

Verified by Experts

माना एक शंकु (V,AB) का शीर्ष V, आधार की त्रिज्या $r_{2}$ और तिर्यक ऊंचाई $l_{2}$ है । इस शंकु के शीर्ष V से $h_{1}$ नीचे स्थित बिन्दु O' से आधार के समान्तर एक शंकु (V,CD) काटा गया है जिसकी त्रिज्या $r_{1}$ तथा तिर्यक ऊंचाई $l_{1}$ है ।
बिन्दु D से आधार पर लम्ब DE खींचा ।

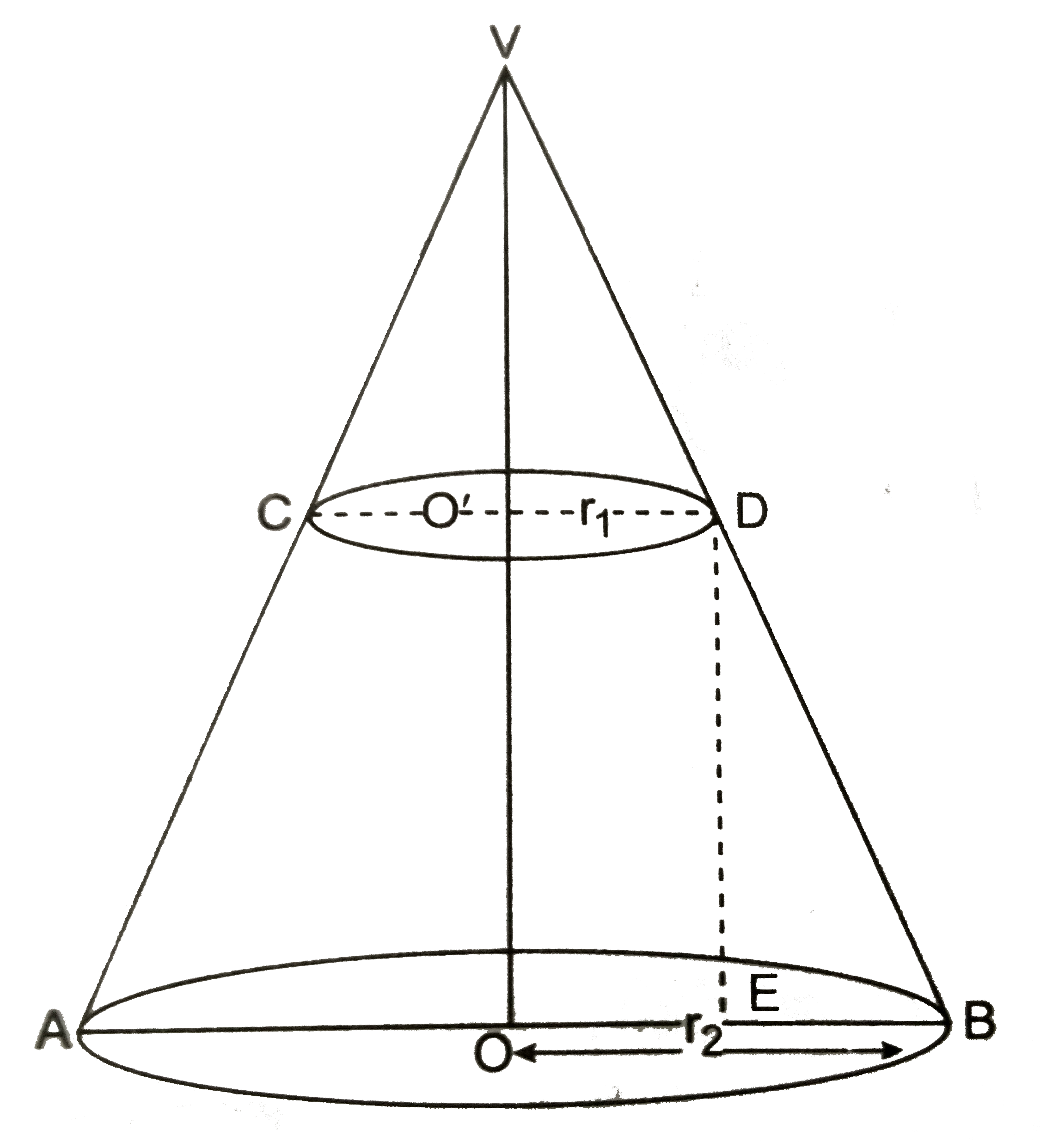
$Δ V O' D$ तथा $Δ D E B$ में ,
$∠ V O' D = ∠ D E B$
(VO और DE दोनों ही आधार पर लम्बवत् है)
$∠ V D O' = ∠ D B E$
(दोनों शंकुओं के आधार परस्पर समान्तर है )
$∴ Δ V O' D$ और $Δ D E B$ समरूप है ,
$\frac{V D}{B D} = \frac{O' D}{E B}$
या $\frac{l_{1}}{l} = \frac{O' D}{O B - O E} = \frac{O' D}{O B - O' D}$
जबकि $B D = l =$ छिन्नक की तिर्यक ऊंचाई
$\Rightarrow \frac{l_{1}}{l} = \frac{r_{1}}{r_{2} - r_{1}} \Rightarrow l_{1} = (\frac{r_{1}}{r_{2} - r_{1}}) l ... ... 1$
छिन्नक का वक्रपृष्ठीय क्षेत्रफल = शंकु (V,AB) का वक्रपृष्ठ- शंकु (V,CD) का वक्रपृष्ठीय
$= π r_{2} l_{2} - π r_{1} l_{1} = π r_{2}$
$= π r_{2} l_{1} + π r_{2} (B D) - π r_{1} l_{1}$
$= π (r_{2} - r_{1}) + π r_{2} l$
(जहाँ $B D = l =$ छिन्नक की तिर्यक ऊंचाई है ।)
$= π (r_{2} - r_{1}) (\frac{r_{1}}{r_{2} - r_{1}}) l + π r_{2} l$
[ समीकरण (1) से ]
$= π r_{1} l + π r_{2} l$
अतः छिन्नक का वक्र पृष्ठीय क्षेत्रफल $= π (r_{1} + r_{2}) l$
यही सिद्ध करना था ।
और छिन्नक का सम्पूर्ण पृष्ठ = वक्रपृष्ठ+ इससे सिरे का क्षेत्रफल + दूसरे सिरे का क्षेत्रफल
$= π (r_{1} + r_{2}) l + π r_{1}^{2} + π r_{2}^{2}$
$= π (r_{1} + r_{2}) l + π (r_{1}^{2} + r_{2}^{2})$
यही सिद्ध करना था ।

|

Updated on:21/07/2023

Class 10 MATHS SURFACE AREAS AND VOLUMES

Topper's Solved these Questions

Similar Questions

NOOTAN HINDI-पृष्ठीय क्षेत्रफल और आयतन -ए०न०सी०ई०आर०टी० प्रश्न (प्रश्नावली 13.5)

Home
Ask Doubt
Profile