एक समकोण त्रिभुज , जिसकी भुजाएँ 3 सेमी और 4 सेमी है ( कारण के अतिरिक्त) , को उसके कारण के परितः घुमाया जाता है । इस प्रकार प्राप्त द्वि- शंकु (double cone) के आयतन और पृष्ठीय क्षेत्रफल ज्ञात कीजिए (π का मान जो भी उपयुक्त लगे , प्रयोग कीजिए )
समकोण ΔABC में ∠B=90∘,AB=4 सेमी , BC=3 सेमी
तब ,ΔABC का क्षेत्रफल =3×42=6 वर्ग सेमी
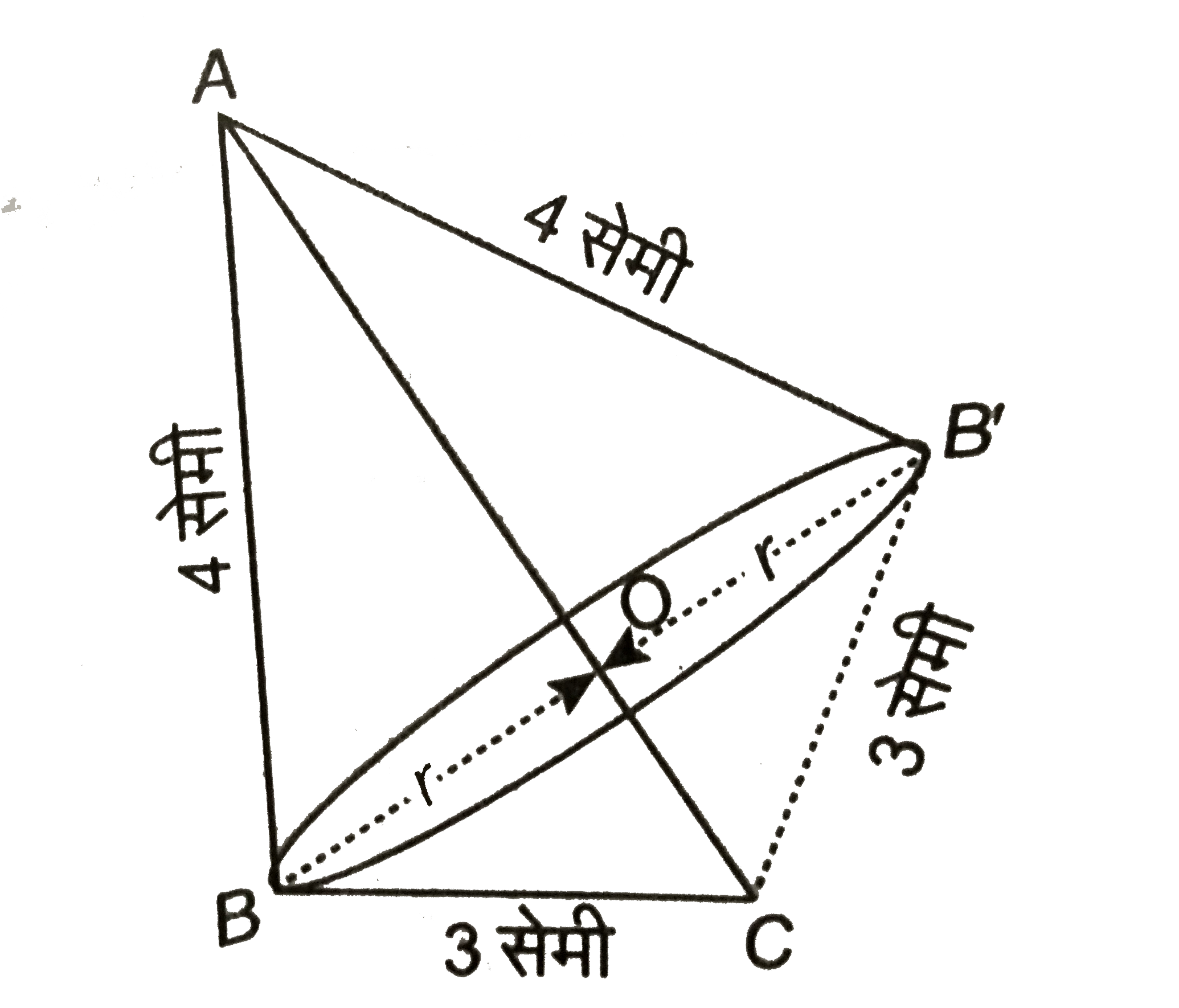
कर्ण AC=√AB2+BC2
=√(4)2+(3)2)=√25=5
AC पर BOB' लम्ब है ,यदि BO=r, हो , तो ΔABC का क्षेत्रफायल =AC×BO2=52BO=52r
तब , 52r=6
(becuase52r और 6 दोनों ΔABC के क्षेत्रफल है ।)
∴r=6×25=2.4 सेमी
अतः समकोण ΔABC के परिक्रमण से बने द्वि - शंकु की त्रिज्या r=2.4 सेमी है ।
तब द्विशंकु ( दोनों शंकुओं ) का आयतन
= शंकु (A,BB') का आयतन + शंकु (C,BB')का आयतन
=12πr2(AO)+13πr2(OC)
=13πr2(AO+OC)
=13πr2(AC)
[∵AO+OC=AC]
=13π×(2.4)2×5=9.6π घन सेमी
9.6×3.14 घन सेमी
=30.144 घन सेमी
और द्विशंकु (दोनों शंकुओं) का पृष्ठीय क्षेत्रफल = शंकु (A,BB' ) का वक्रपृष्ठ + शंकु (C,BB') का वक्रपृष्ठ
πr(AB)+πr(BC)=πr(AB+BC)
=3.14×2.4×(4+3)=3.14×2.4×7
=52.75 वर्ग सेमी
अतः द्विशंकु का आयतन =30.144 घन सेमी
तथा पृष्ठीय क्षेत्रफल =52.75 वर्ग सेमी ( लगभग ) ।
Topper's Solved these Questions
- पृष्ठीय क्षेत्रफल और आयतन BOOK - NOOTAN HINDICHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - विविध प्रश्नावली (अतिलघु उत्तरीय प्रश्न)
10 Videos
- पृष्ठीय क्षेत्रफल और आयतन BOOK - NOOTAN HINDICHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - लघु उत्तरीय प्रश्न
10 Videos
- पृष्ठीय क्षेत्रफल और आयतन BOOK - NOOTAN HINDICHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - ए०न०सी०ई०आर०टी० प्रश्न (प्रश्नावली 13.4)
5 Videos
- निर्देशांक ज्यामितिBOOK - NOOTAN HINDICHAPTER - निर्देशांक ज्यामितिEXERCISE - बहुविकल्पीय प्रश्न
7 Videos
- प्रायिकता BOOK - NOOTAN HINDICHAPTER - प्रायिकता EXERCISE - बहुविकल्पीय प्रश्न
7 Videos
Similar Questions
एक धातु के ठोस गोले जिसकी त्रिज्या 9 सेमी है , को पिघलाकर 9 सेमी त्रिज्या का ठोस बेलन बनाया गया है , बेलन की ऊंचाई ज्ञात कीजिए ।
View Solution28 सेमी व्यास और 72 सेमी ऊंचाई की एक बाल्टी पानी से भरी है । इसका पानी 66 सेमी लम्बी और 28 सेमी चौड़ी आयताकार टंकी में खाली कर दिया जाता है । टंकी में पानी की सतह की ऊंचाई ज्ञात कीजिए ।
View Solutionपानी पीने वाला एक गिलास 14 सेमी ऊंचाई वाले एक शंकु के छिन्नक के आकार का है । दोनों वृत्ताकार सिरों के व्यास 4 सेमी और 2 सेमी है । इस गिलास की धारिता ज्ञात कीजिए ।
View Solutionबिंदु (3, 4) की x-अक्ष से दूरी है :
View Solutionकिसी निश्चित घटना की प्रायिकता है :
View Solutionएक त्रिभुज ABC में मध्यिकाएँ AD ,BE और CF एक बिंदु G से गुजरती है। यदि AD=9 सेमी ,GE=4.2 सेमी और GC=6 सेमी ,तो AG , BE औरFG की लम्बाइयों के मान ज्ञात कीजिए।
View Solutionदो स्थिर बिंदुओं A और B के निर्देशांक क्रमश :(5,3) और (3,−2) है । बिंदु P इस प्रकार गमन करता है कि त्रिभुज PAB का क्षेत्रफल 9 वर्ग क्षेत्रफल वर्ग मात्रक रहता है । बिंदु P का बिन्दुपथ ज्ञात कीजिए ।
View Solutionएक आयत की भुजाएँ x=2,x=−4,y=3 और y=−5 है। इसके विकर्णों के समीकरण ज्ञात कीजिए ।
View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionएक शंकु की त्रिज्या 7 सेमी और ऊँचाई 9 सेमी है। इसका आयतन समान त्रिज्या वाले एक दूसरे शंकु के वक्र पृष्ठ के बराबर होता है। इस शंकु को तिर्यक ऊँचाई ज्ञात कीजिए।
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का पृष्ठीय क्षेत्रफल#!#महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का पृष्ठीय क्षेत्रफल#!#महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु का आयतन#!#शंकु के आयतन पर आधारित महत्वपूर्ण प्रश्न
View Solutionपृष्ठीय क्षेत्रफल और आयतन|शंकु के पृष्ठीय क्षेत्रफल और आयतन पर आधारित प्रशन
View Solutionपृष्ठीय क्षेत्रफल और आयतन के महत्वपूर्ण प्रश्न
View Solution