दर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें, तो वह एक समचतुर्भुज होता है।
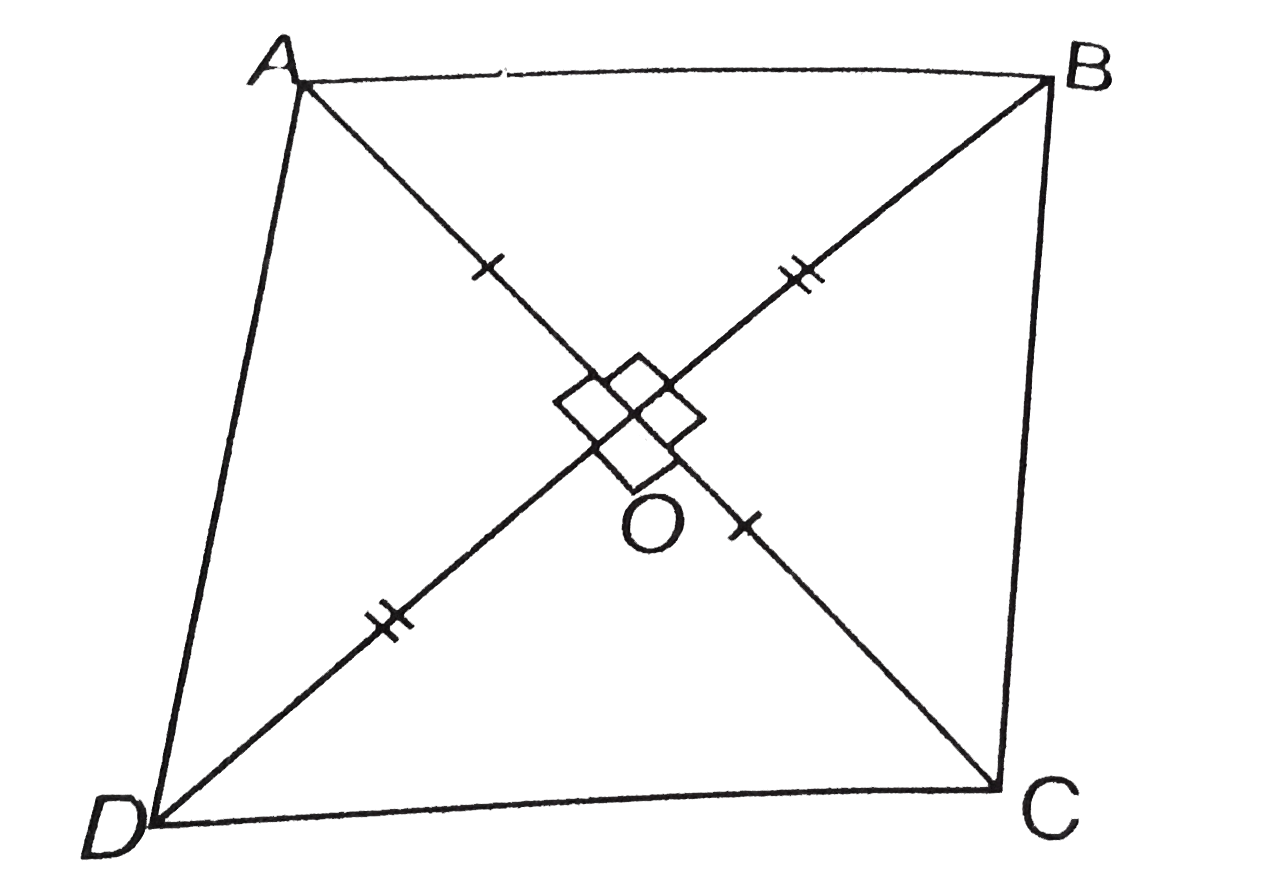
एक चतुर्भुज ABCD जिसके विकर्ण AC और BD एक –दूसरे को समकोण पर समद्विभाजित करते हैं
अर्थातOA=OC
औरOB=OD
और
∠AOD=∠AOB=∠COD=∠BOC=90∘
दर्शाना है:
ABCD एक समुचतुर्भुज है।
उपपति
ΔOAB और ΔODC में
∵⎧⎪⎨⎪⎩OA=OCOB=OD∠AOB=∠COD (दिया है)
∴ΔOAB=ΔOCD (S.A.S. से)
∴AB=CD (c.p.c.t)…….1
पुन: ΔOAD और ΔOBC में
∵⎧⎪⎨⎪⎩OA=OCOD=OB∠AOD=∠BOC(दिया है)
∴ΔOAD=ΔOCB (S.A.S. से )
∴AD=BC(c.p.c.t.)……….2
इसी प्रकार सिद्ध कर सकते हैं कि
AB=AD
CD=BC………………3
अतः 1,2 और 3 से
AB=BC=AD=CD
अतः ABCD एक समचतुर्भुज है।
Topper's Solved these Questions
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8.2
7 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8B
15 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - दीर्घ उत्तरीय प्रश्न
5 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
8 Videos
Similar Questions
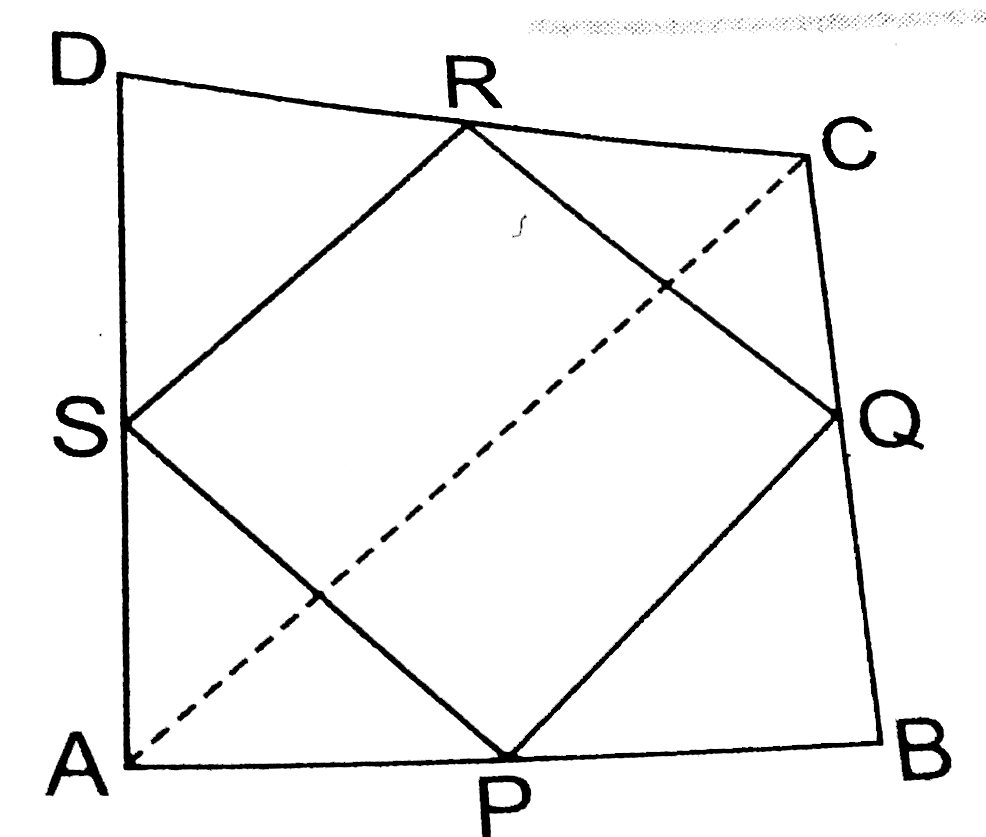
ABCD एक चतुर्भुज है जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य बिंदु हैं । AC उसका एक विकर्ण है। दर्शाइए कि:
(i) SR∣∣AC और SR=12AC है।
(ii) PQ=SR है।
(iii) PQRS एक समांतर चतुर्भुज है।
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionएक समद्विबाहु त्रिभुज ABC की भुजाएं AB और AC बराबर है। D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य बिंदु हैं सिद्ध कीजिए कि-
(i) रेखाखण्ड AD, रेखाखण्ड EF पर लम्ब है।
(ii) रेखाखण्ड AD रेखाखण्ड EF को समद्विभाजित करता है।
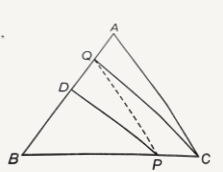
View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
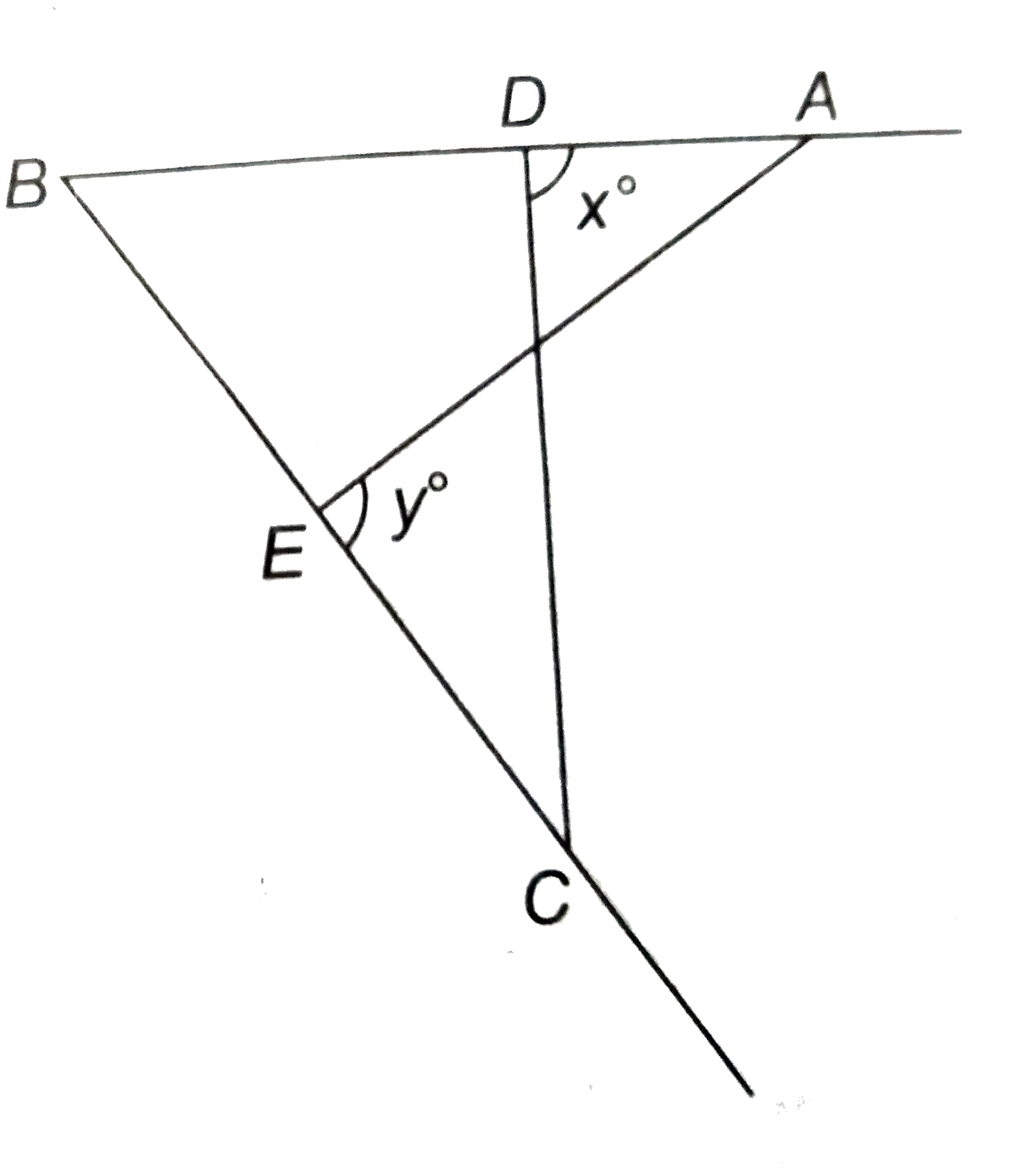
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionदर्शाइए कि सदिश 2ˆi−ˆj+ˆk,ˆi−3ˆj−5ˆk और (3ˆi−4ˆj−5ˆk) एक समकोण त्रिभुज के शीर्षों कि रच्ना करते है।
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionयदि समान्तर चतुर्भुज कि दो आसान भुजाएँ →a तथा →b हो , तो इसका विकर्ण ज्ञात कीजिए।
View Solutionपाँच पासो को एक साथ फेंका गया है। यदि एक पासे पर सम अंक आने को सफलता माना जाये तो अधिकतम 3 सफलताओ कि प्रायिकता ज्ञात करो ।
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionमाना एक दीर्घवृत्त कि नाभियां S तथा S' है तथा इसके लघु अक्ष का कोई एक शीर्ष B है। यदि ΔS'BS एक समकोण त्रिभुज है जिसका समकोण B पर है तथा ΔS'BS का क्षेत्रफल 8 वर्ग इकाई है, तो दीर्घवृत्त की एक नाभिलम्ब जीवा की लम्बाई है
View Solutionदर्शाइए कि धनात्मक सम पूर्णांक 4q या 4q+2 के रूप का होता है, जहाँ एक पूर्णाक है।
View Solutionयदि दो समकोण त्रिभुजों में से एक त्रिभुज की एक भुजा और एक न्यूनकोण दूसरे त्रिभुज की एक भुजा और तदनुरूपी कोण के बराबर हो, तो दोनों त्रिभुज परस्पर क्या होंगे ?
View SolutionOne side of a rhombus is 6.5 cm and one of it’s diagonal is 12 cm. What is the area of the rhombus?
किसी समचतुर्भुज की एक भुजा 6.5 सेमी की है तथा इसका एक विकर्ण 12 सेमी का है | इस समचतुर्भुज का क्षेत्रफल ज्ञात करें |
View SolutionThe side of a rhombus is 5 cm and one of its diagonal is 8 cm. What is the area of the rhombus?
एक समचतुर्भुज की भुजा 5 सेमी तथा इसका एक विकर्ण 8 सेमी का है | इस समचतुर्भुज का क्षेत्रफल ज्ञात करें |
View Solution