दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और परस्पर लम्बवत समद्विभाजित करें तो वह एक वर्ग होता है।
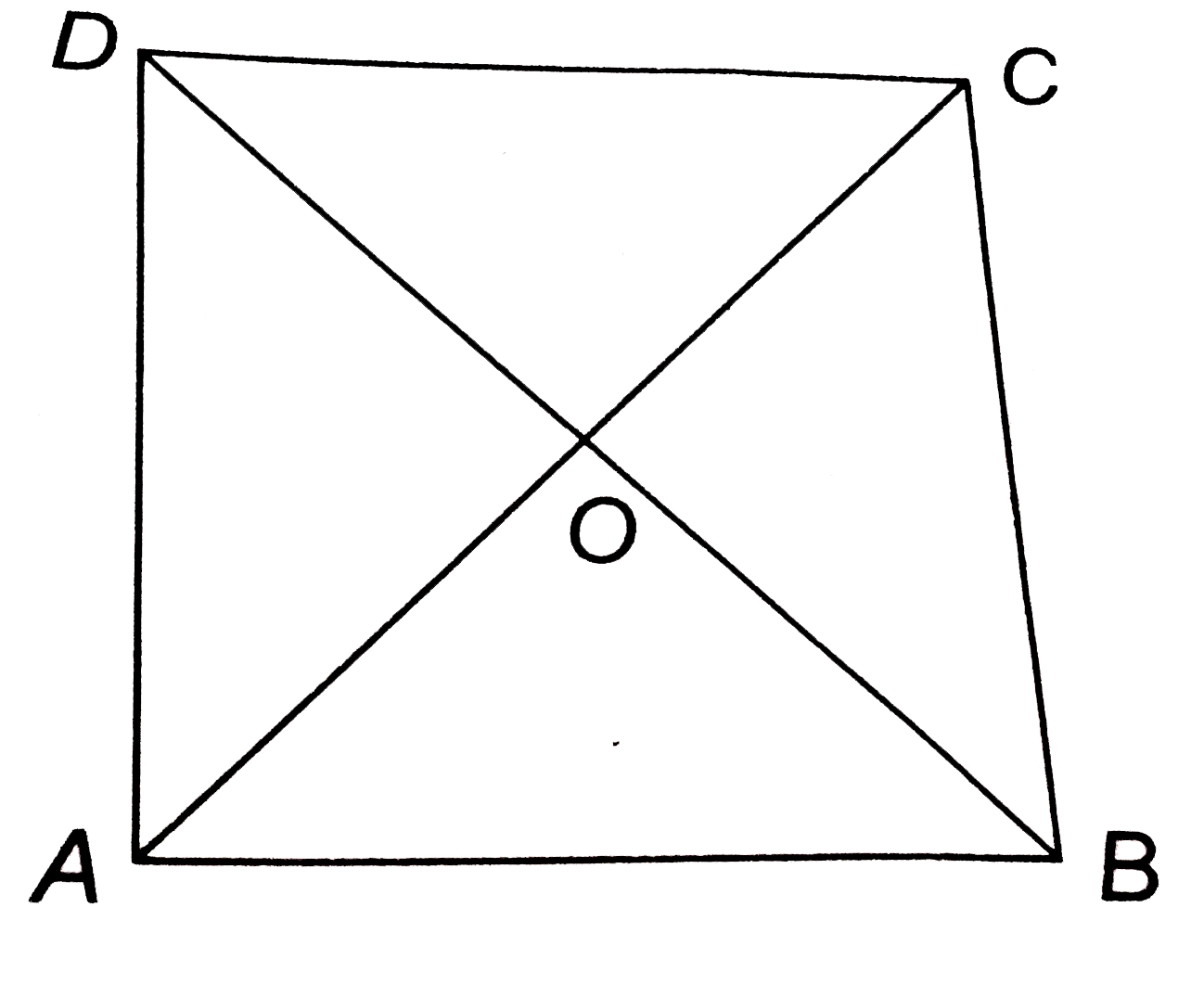
दिया है : एक चतुर्भुज ABCD में विकर्ण और हैं।
दर्शाना है: चतुर्भुज ABCD एक वर्ग हैं
उपपत्ति: और में
(दिया है)
(दिया है)
(शीर्षाभिमुख कोण)
(S.A.S से )
(c.p.c.t)……………1
परंतु ये एकांतर कोण है
इसी प्रकार
अतः ABCD एक समांतर चतुर्भुज है।
अब हम सिद्ध करेगें कि यह एक वर्ग है।
और में
(उभयनिष्ठ)
(प्रत्येक दिया है)
और
(समांतर चतुर्भुजों के विकर्ण एक-दूसरे को समद्विभाजित करते हैं)
(S.A.S से )
(c.p.c.t)
परंतु और
(समांतर चतुर्भुज की सम्मुख भुजाएं बराबर होती हैं)
……….. 1
अब और में
(उभयनिष्ठ)
(समांतर चतुर्भुज की सम्मुख भुजाएं बराबर होती हैं)
और (दिया है)
(S.S.S से )
(c.p.c.t)
अर्थात
(समांतर चतुर्भुज के अन्तः कोणों के योग से)
या
इसी प्रकार
या
अतः एक वर्ग है।
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8.27videos
चतुर्भुज
- BOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली24videos
चतुर्भुज
- BOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8B15videos
चतुर्भुज
- BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - दीर्घ उत्तरीय प्रश्न5videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )8videos
त्रिभुज
Similar Questions
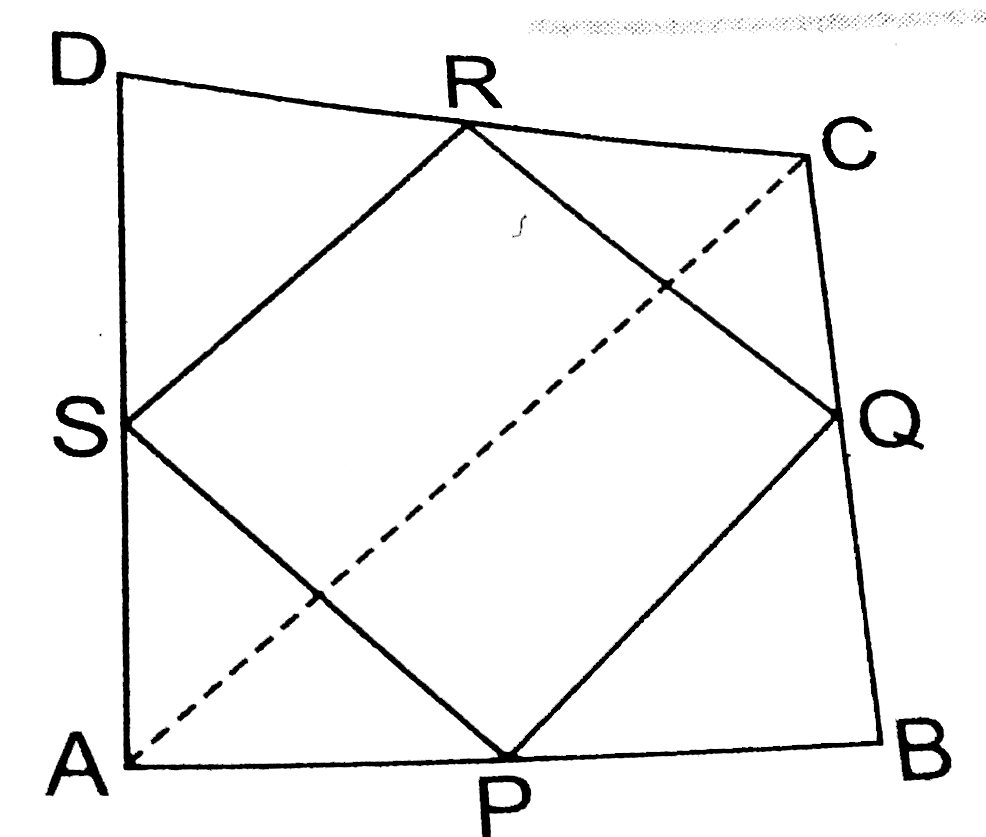
ABCD एक चतुर्भुज है जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य बिंदु हैं । AC उसका एक विकर्ण है। दर्शाइए कि:
(i) SR∣∣AC और SR=12AC है।
(ii) PQ=SR है।
(iii) PQRS एक समांतर चतुर्भुज है।
 04:23View Solution
04:23View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
04:27View Solutionएक समद्विबाहु त्रिभुज ABC की भुजाएं AB और AC बराबर है। D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य बिंदु हैं सिद्ध कीजिए कि-
(i) रेखाखण्ड AD, रेखाखण्ड EF पर लम्ब है।
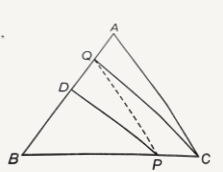
(ii) रेखाखण्ड AD रेखाखण्ड EF को समद्विभाजित करता है।04:17View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
 03:43View Solution
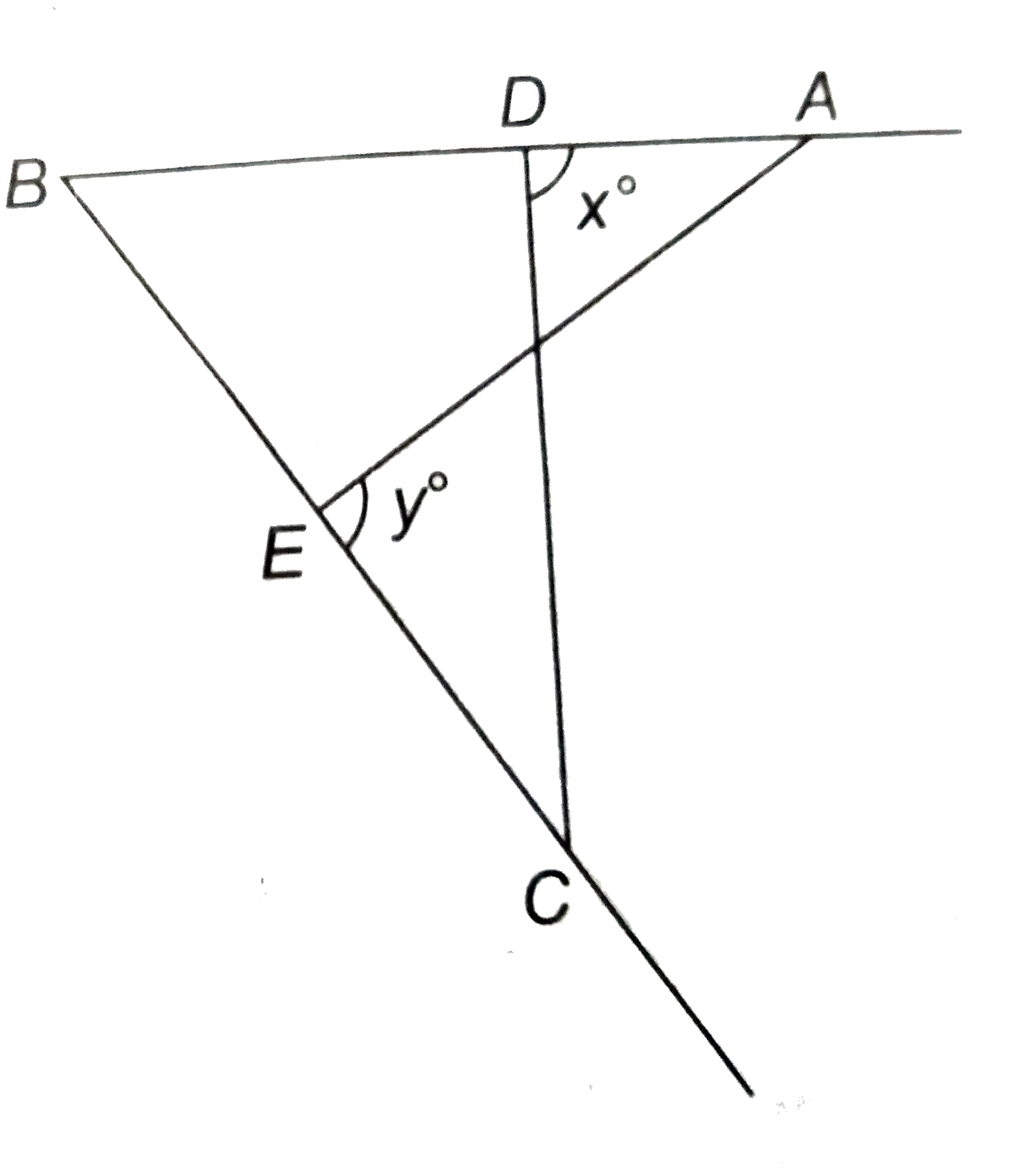
03:43View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
 03:32View Solution
03:32View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
05:05View Solutionयदि किसी चतुर्भुज की भुजाओं को क्रमानुसार दिशा व परिमाण में निरूपित करने वाले सदिश ¯a,¯b,¯c,¯d हों तों सिद्ध कीजिए कि चतुर्भुज एक समांतर चतुर्भुज होगा यदि और केवल यदि ¯a+¯c=¯0 जिससे ¯b+¯d=¯0
04:18View Solutionसदिश विधि से सिद्ध करें कि यदि किसी त्रिभुज दो मध्यिकाएँ बराबर हों, तो त्रिभुज समद्विबाहु होता है |
03:23View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
03:55View Solutionयदि समान्तर चतुर्भुज कि दो आसान भुजाएँ →a तथा →b हो , तो इसका विकर्ण ज्ञात कीजिए।
01:53View Solutionमाना एक ऊर्ध्वाधर मीनार AB ऐसी है कि उसका सिरा A भूमि पर है। माना AB का मध्य-बिन्दु C है और भूमि पर स्थित बिन्दु P ऐसा है कि AP=2AB यदि ∠BPC=β है, तो tanβ बराबर है
04:01View Solutionयदि एक सममित आव्यूह A तथा एक विषम सममित आव्यूह B इस प्रकार है कि A+B=[235−1] तो AB बराबर है
03:46View Solutionयदि A एक वर्ग आव्यूह है, तब A+AT होगा
01:39View Solutionदर्शाइए कि धनात्मक सम पूर्णांक 4q या 4q+2 के रूप का होता है, जहाँ एक पूर्णाक है।
01:56View Solutionयदि दो समकोण त्रिभुजों में से एक त्रिभुज की एक भुजा और एक न्यूनकोण दूसरे त्रिभुज की एक भुजा और तदनुरूपी कोण के बराबर हो, तो दोनों त्रिभुज परस्पर क्या होंगे ?
View SolutionThe area of square is 200m^2 . A new square is formed in such a way that the length of its diagonal is sqrt2 times of the given square. Then the area of the new square formed is- एक वर्ग का क्षेत्रफल 200 वर्ग मीटर है। एक नया वर्ग इस प्रकार बनाया गया है कि उसके विकर्ण की लंबाई पहले वर्ग के विकर्ण की sqrt2 गुना के बराबर है, नये वर्ग का क्षेत्रफल है-
View Solution

