दिया है:
ABCD एक आयत है।
∴AB=CD और BC=AD…………..1
सिद्ध करना है:
(i) ABCD एक वर्ग है।
अर्थात
AB=BC=CD=DA
(ii) विकर्ण BD,∠B और ∠D दोनों को समद्विभाजित करता है।
उपपत्ति :
(i) ΔADC और ΔABC में
AB∣∣DC और तिर्यक रेखा AC इनको काटती है।
∵⎧⎪⎨⎪⎩∠DAC=∠BAC∠DCA=∠BCAAC=CA (उभयनिष्ठ)
∴ΔADC=ΔABC (A.S.A. से )
∴AD=AB (c.p.c.t)
और CD=BC…………2
अतः समीकरण 1 और 2 से
AB=BC=AD=CD
∴ABCD एक वर्ग है।
(ii) ΔAOB और ΔCOB में
∵⎧⎪⎨⎪⎩AB=BCBO=OBOA=OC(एक वर्ग की भुजाएं)
(उभयनिष्ठ)
( ∵ वर्ग के विकर्ण एक-दूसरे को समद्विभाजित करते हैं)
∴ΔAOB=ΔCOB
(S.S.S. से )
∴∠OBA=∠OBC
(c.p.c.t)
अतः BO या BD,∠B को समद्विभाजित करती है।
इसी प्रकार ΔAOD और ΔCOD में
∵⎧⎪⎨⎪⎩AD=CDOD=DOOA=OC (वर्ग की भुजाएं)
(उभयनिष्ठ)
( ∵ वर्ग के विकर्ण एक-दूसरे की समद्विभाजित करते है।)
∴ΔAOD=ΔCOD
(S.S.S से)
∴∠ADO=∠CDO
अतः DO या DB,∠D को समद्विभाजित करती है।
दिया है:
ABCD एक आयत है।
∴AB=CD और BC=AD…………..1
सिद्ध करना है:
(i) ABCD एक वर्ग है।
अर्थात
AB=BC=CD=DA
(ii) विकर्ण BD,∠B और ∠D दोनों को समद्विभाजित करता है।
उपपत्ति :
(i) ΔADC और ΔABC में
AB∣∣DC और तिर्यक रेखा AC इनको काटती है।
∵⎧⎪⎨⎪⎩∠DAC=∠BAC∠DCA=∠BCAAC=CA (उभयनिष्ठ)
∴ΔADC=ΔABC (A.S.A. से )
∴AD=AB (c.p.c.t)
और CD=BC…………2
अतः समीकरण 1 और 2 से
AB=BC=AD=CD
∴ABCD एक वर्ग है।
(ii) ΔAOB और ΔCOB में
∵⎧⎪⎨⎪⎩AB=BCBO=OBOA=OC(एक वर्ग की भुजाएं)
(उभयनिष्ठ)
( ∵ वर्ग के विकर्ण एक-दूसरे को समद्विभाजित करते हैं)
∴ΔAOB=ΔCOB
(S.S.S. से )
∴∠OBA=∠OBC
(c.p.c.t)
अतः BO या BD,∠B को समद्विभाजित करती है।
इसी प्रकार ΔAOD और ΔCOD में
∵⎧⎪⎨⎪⎩AD=CDOD=DOOA=OC (वर्ग की भुजाएं)
(उभयनिष्ठ)
( ∵ वर्ग के विकर्ण एक-दूसरे की समद्विभाजित करते है।)
∴ΔAOD=ΔCOD
(S.S.S से)
∴∠ADO=∠CDO
अतः DO या DB,∠D को समद्विभाजित करती है।
Topper's Solved these Questions
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8.2
7 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8B
15 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - दीर्घ उत्तरीय प्रश्न
5 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
8 Videos
Similar Questions
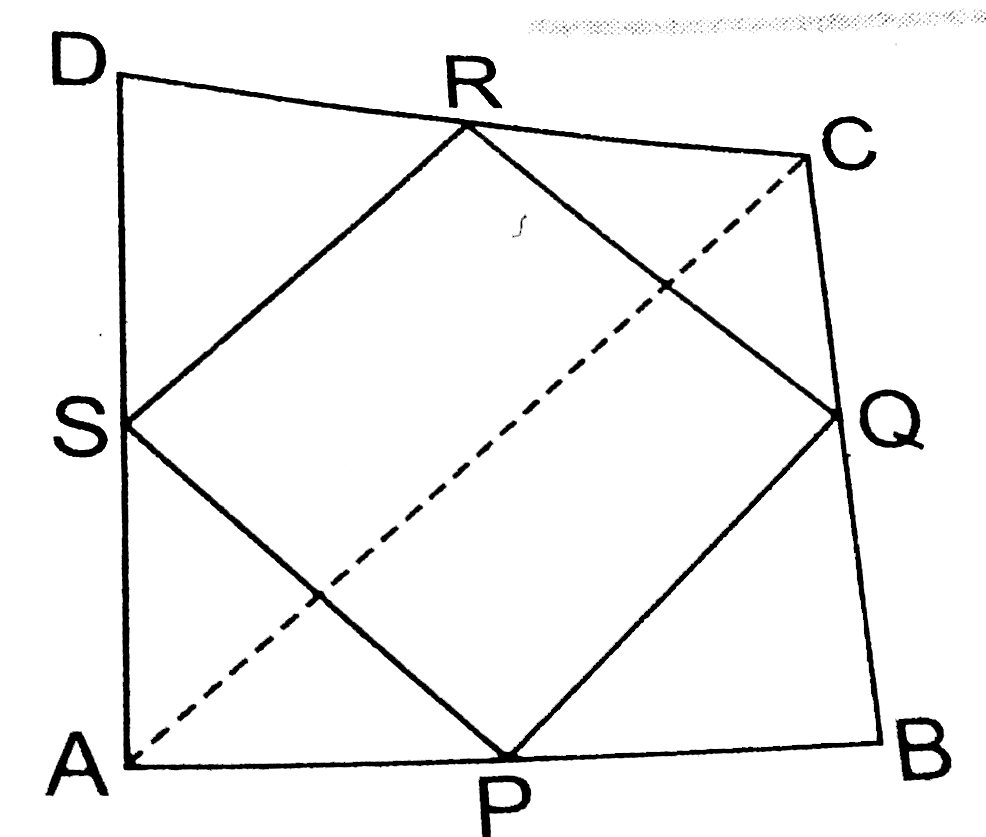
ABCD एक चतुर्भुज है जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य बिंदु हैं । AC उसका एक विकर्ण है। दर्शाइए कि:
(i) SR∣∣AC और SR=12AC है।
(ii) PQ=SR है।
(iii) PQRS एक समांतर चतुर्भुज है।
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionएक समद्विबाहु त्रिभुज ABC की भुजाएं AB और AC बराबर है। D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य बिंदु हैं सिद्ध कीजिए कि-
(i) रेखाखण्ड AD, रेखाखण्ड EF पर लम्ब है।
(ii) रेखाखण्ड AD रेखाखण्ड EF को समद्विभाजित करता है।
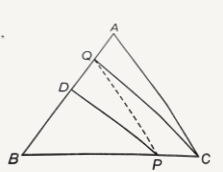
View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
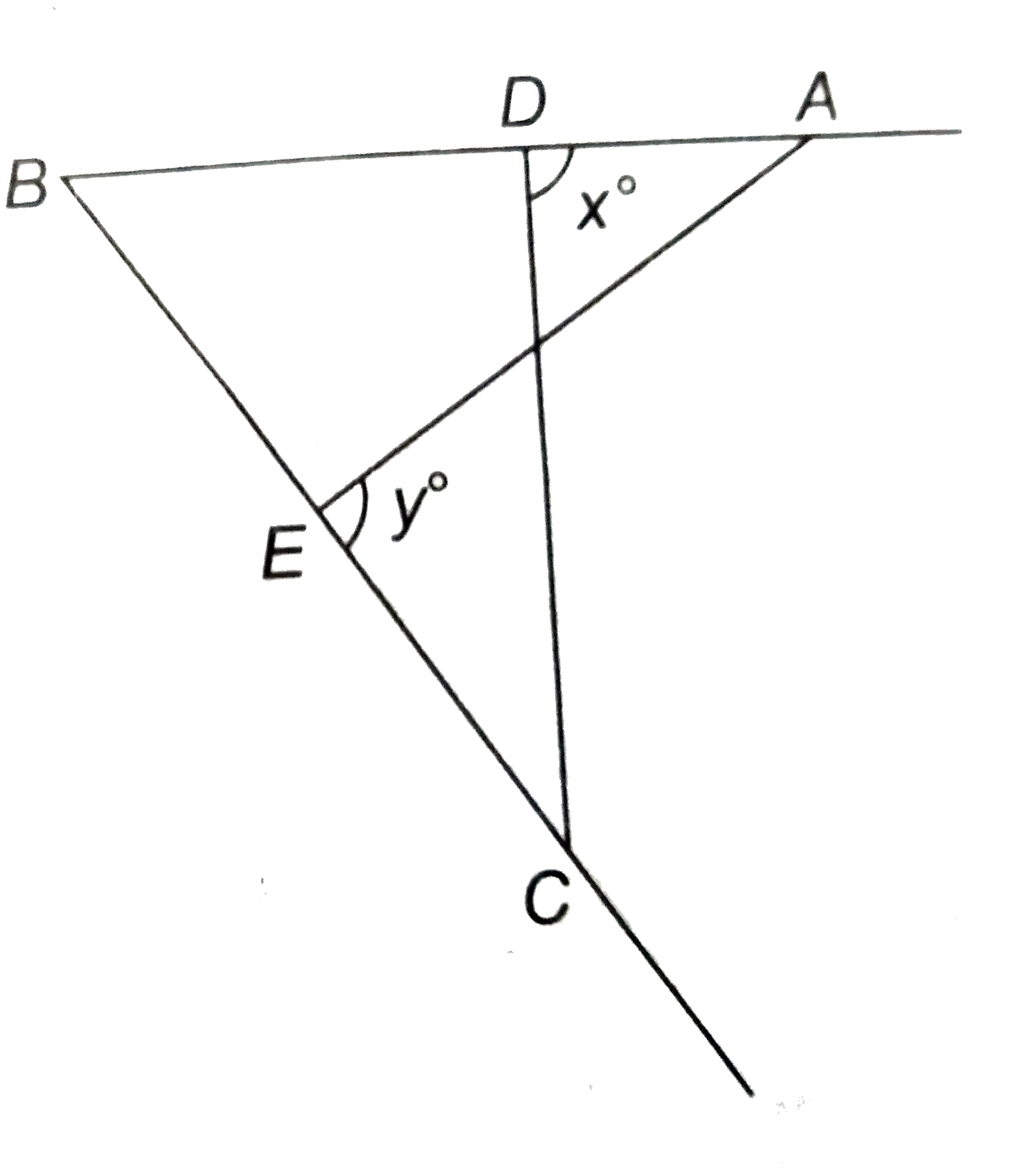
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
View SolutionWhich of the following symbols are not acceptable ? (i) ._(35)^(79)Br (ii) .^(79)Br (iii) ._(79)^(35)Br (iv) ._(35)Br
View SolutionThe value of |[a,a+d,a+2d] , [a+d,a+2d,a+3d] , [a+2d,a+3d,a+4d]|+|[b
View SolutionAmongst the species Br^(-), Br, Br^(+), the smallest one in size is ________.
View SolutionIn CH_(3)CH_(2)Br,% of Br is
View Solution.7935Br तथा .79Br मान्य हैं जबकि .3579Br तथा .35Br मान्य नहीं हैं । संपेक्ष में कारण बताइए ।
View SolutionIn CH3CH2Br,% of Br is
View SolutionThe correct order of size among Br^(+), Br, Br^(-)
View Solutionఏ అవయవాలు కవాటాలు కల్గి ఉంటాయి ?br i) గుండెbr ii) ధమనిbr iii) సిరలుbr iV) శోషరస నాళాలు
View Solution1) Fragmentation () a) Planaria br 2) Unripe fruits () b) Yeast br 3) Desire () c) Spirogyra br 4) Reproduction () d) Watermelon br
View Solutionవేర్ల ద్వారా శాఖీయోత్పత్తి జరిపే మొక్కbr i) డాలియాbr ii) ముల్లంగిbr iii) క్యారెట్br iv) క్యాబేజిbr
View Solution[" Which alkyl bromide will yield only one alkene upon "E_(2)" elemination? "],[[" 1) "," ( "" Br "," 2) "," Br "" 3) "," Br "," ( "" ) "," ( Br "]]
View Solution
