ΔABC और ΔDEF में AB=DE,AB∣∣DE,BC=EF और BC∣∣EF हैं शीर्षों A,B और C को क्रमशः शीर्षों D,E और F से जोड़ा जाता है।
(i) चतुर्भुज ABED एक समांतर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समांतर चतुर्भुज है।
(iii) AD∣∣CF और AD=CF है।
(iv) चतुर्भुज ACFD एक समांतर चतुर्भुज है।
(v) AC=DF है।
(vi) ΔABC≅ΔEF है।
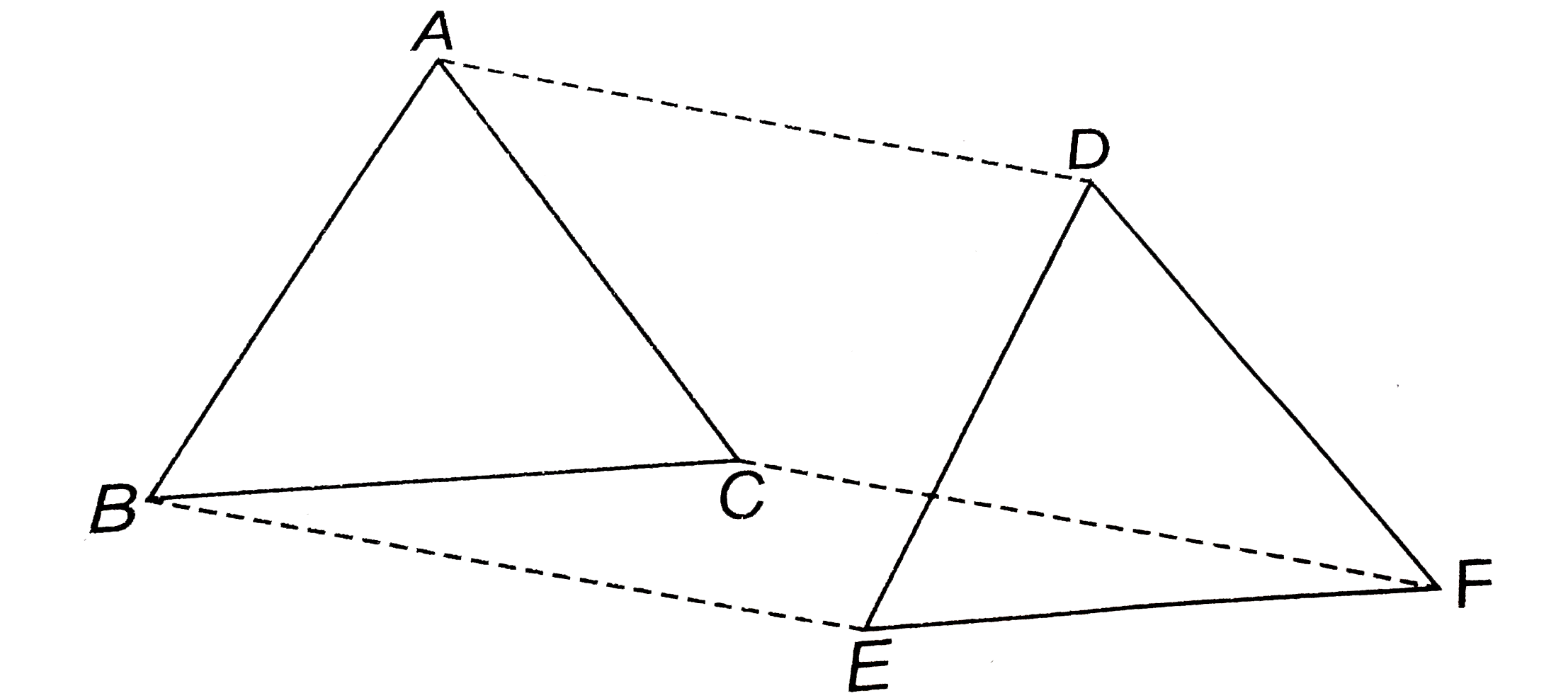
(i) चतुर्भुज ABED में
AB=DE और AB∣∣DE
⇒ सम्मुख भुजाओं का एक युग्म बराबर और समांतर है।
⇒ABED एक समांतर चतुर्भुज है।
(ii) अब चतुर्भुज BEFC में
BC=FE और BC∣∣EF
⇒ सम्मुख भुजाओं का एक युग्म बराबर और समांतर है।
⇒BEFC एक समांतर चतुर्भुज है।
(iii) अब AD=BE और AD∣∣BE…………..1
( ∵ABED एक समांतर चतुर्भुज है)
और CF=BE और CF∣∣BE………..2
( ∵BEFC एक समांतर चतुर्भुज है)
समीकरण 1 और 2 से
AD=CF और AD∣∣CF
(iv) AD=CF और AD∣∣EF
⇒ सम्मुख भुजाओं का एक युग्म बराबर और समांतर है।
⇒ACFD एक समांतर चतुर्भुज है।
(v) ACFD एक समांतर चतुर्भुज है। AC=DF और AC∣∣DF
(vi) ΔABC और ΔDEF में
AB=DE
(समांतर चतुर्भुज ABED की सम्मुख भुजाएं)
BC=EF
(समांतर चतुर्भुज BEFC की सम्मुख भुजाएं)
और CA=FD
(समांतर चतुर्भुज ACFD की सम्मुख भुजाएं)
ΔABC≅ΔDEF (S.S.S. से )
Topper's Solved these Questions
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:प्रश्नावली 8.2
Explore 7 Videos
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:विविध प्रश्नावली
Explore 24 Videos
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:प्रश्नावली 8B
Explore 15 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:दीर्घ उत्तरीय प्रश्न
Explore 5 Videos
- त्रिभुज Book:NOOTAN HINDIChapter:त्रिभुज Exercise:विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
Explore 8 Videos
Similar Questions
ABCD एक चतुर्भुज है जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य बिंदु हैं । AC उसका एक विकर्ण है। दर्शाइए कि:
(i) SR∣∣AC और SR=12AC है।
(ii) PQ=SR है।
(iii) PQRS एक समांतर चतुर्भुज है।
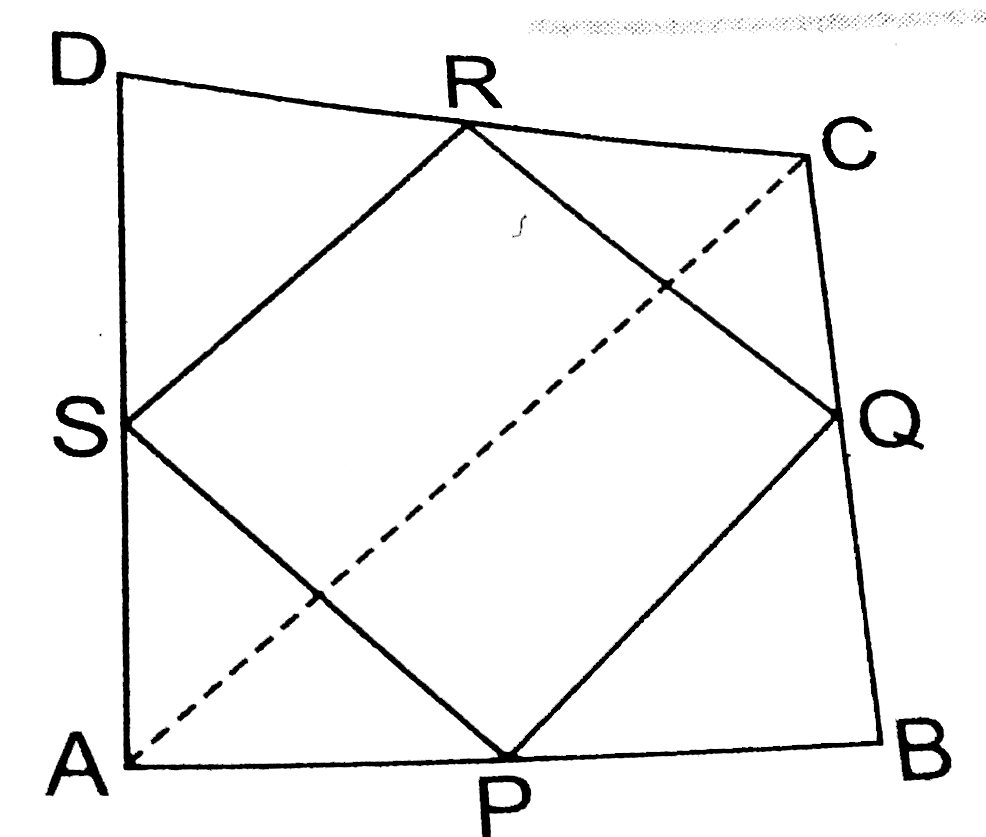
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionएक समद्विबाहु त्रिभुज ABC की भुजाएं AB और AC बराबर है। D,E और F क्रमशः भुजाओं BC,CA और AB के मध्य बिंदु हैं सिद्ध कीजिए कि-
(i) रेखाखण्ड AD, रेखाखण्ड EF पर लम्ब है।
(ii) रेखाखण्ड AD रेखाखण्ड EF को समद्विभाजित करता है।
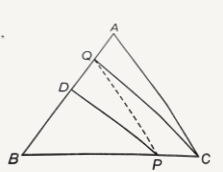
View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
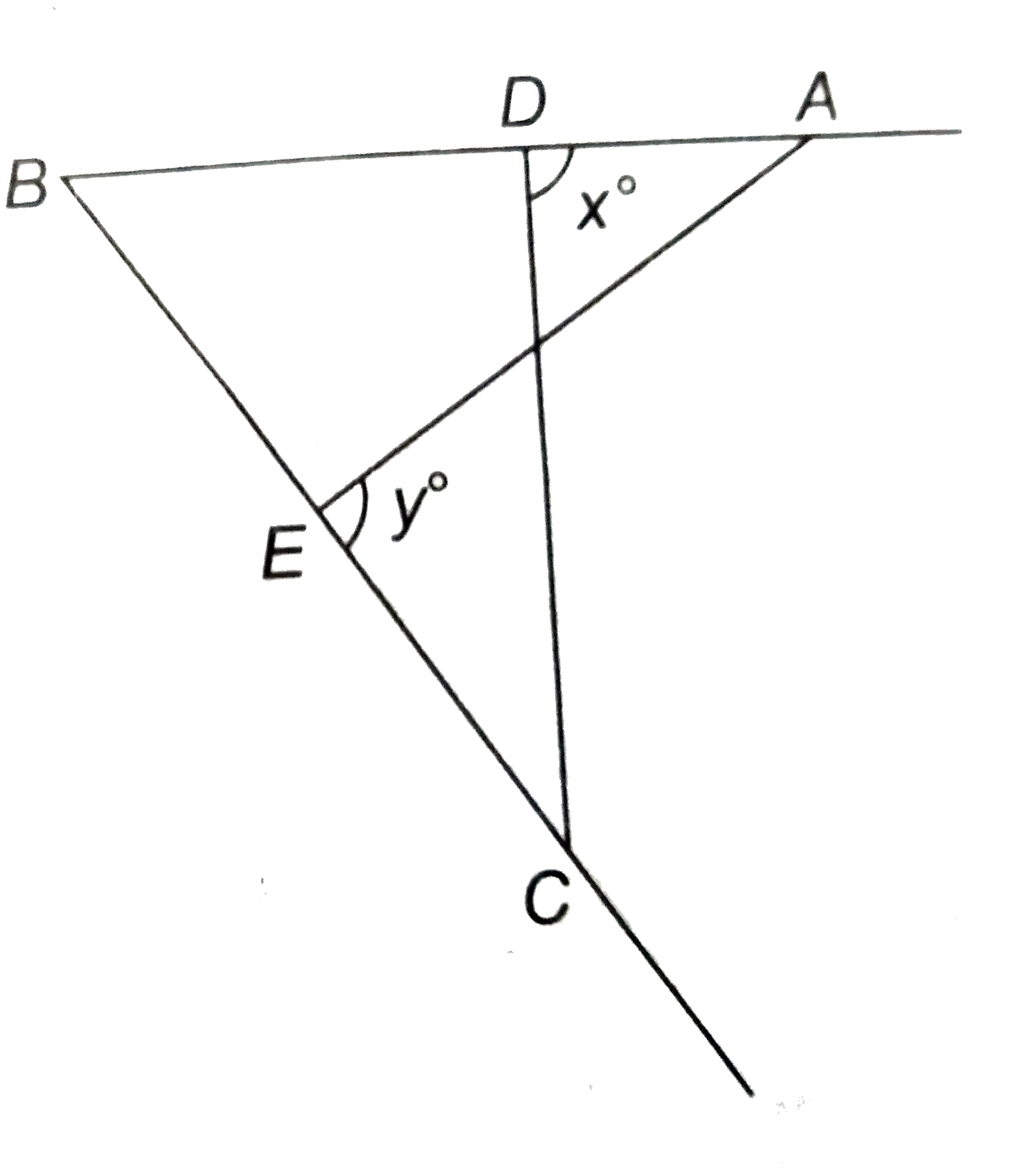
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View SolutionIn ΔABCandΔDEF,AB=DE,AB||DE,BC=EFandBC||EF Vertices A,B and C are joined to vertices D , E and F respectively show that
quadrilateral ABED is a parallelogram
quadrilateral BEFC is a parallelogram
AD∣∣CFandAD=CF
quadrilateral ACFD is a parallelogram
AC=DF
ΔABC≈ΔDEF.
View Solutionनिम्नलिखित के उत्तर दीजिए और उनके कारण भी दीजिए :
(i ) क्या AB = BC है?
(ii ) क्या AB = DC है?
(iii ) क्या DE = AF है?
(iv ) क्या EF = AB है?
(v ) क्या BC = EF है?
(vi ) क्या AB = DC = EF है?
View SolutionRevision|चतुर्भुज#!#समांतर चतुर्भुज#!#महत्वपूर्ण प्रश्न
View SolutionThe length of two sides of a parallelogram are 3cm and 10 cm. What is the sum of the squares of diagonals of the parallelogram ? एक समांतर चतुर्भुज के दो भुजाओं की लंबाई 3 सेमी और 10 सेमी है। समांतर चतुर्भुज के विकर्णों के वर्गों का योग क्या होगा ?
View SolutionA circle is inscribed in a quadrilateral ABCD touching AB,BC, CD and AD at the points P,Q,R and S, respectively, and ∠B=90∘. If AD = 24 cm, AB=27 cm and DR = 6cm, then what is the circumference of the circle ?
एक वृत्त चतुर्भुज ABCD के भीतर स्थित है जो AB, BC, CD और AD को क्रमशः P, Q, R और S पर स्पर्श करता है और ∠B=90∘ है | यदि AD = 24 सेमी, AB=27 सेमी और DR = 6 सेमी है, तो वृत्त की परिधि ज्ञात करें |
View SolutionIf in △ABC, D and E are the points on AB and BC respectively such that DE||AC, and AD:AB =3:8, then (area of △BDE ) : (area of quadrilateral DECA) = ?
यदि त्रिभुज ABC में, D और E क्रमशः AB और BC पर स्थित ऐसे बिंदु हैं कि DE||BC है और AD:AB = 3:8 है, तो (△BDE का क्षेत्रफल ) : ( चतुर्भुज DECA का क्षेत्रफल ) ज्ञात करें |
View SolutionA circle inscribed in a triangle ABC touches its sides AB, BC and AC at the points D, E and F, respectively. If AB = 18cm, BC = 15cm and AC = 13 cm then the value of of AD+BE+CF is: एक त्रिभुज ABCमें अंकित एक वृत्त क्रमशः AB, BC और AC के भुजाओं D, E और F को स्पर्श करता है। यदि AB = 18 सेमी, BC = 15 सेमी और AC = 13 सेमी है तो AD+ BE+ CF का मान है:
View Solutionचतुर्भुज |चतुर्भुज का कोण योग गुण |चतुर्भुज के प्रकार |समांतर चतुर्भुज के गुण|प्रमेय|सारांश
View SolutionIn triangle ABC, D and E are two points on the sides AB and AC respectively so that DE||BC and AD/BD=3/4 . The ratio of the area of triangle ABC to the area of trapezium DECB is: त्रिभुज ABC में, AB और AC भुजाओं पर 2 बिंदु क्रमशः D और E इस तरह है कि DE||BC और AD/BD=3/4 है| triangle ABC क्षेत्रफल का समलंब चतुर्भुज DECB के क्षेत्रफल से अनुपात है :
View Solutionसमांतर चतुर्भुज के गुण
View Solution
