ABCD एक समचतुर्भुज है। RABS एक सरल रेखा इस प्रकार है कि RA=AB=BS है । सिद्ध कीजिए कि RD और SC बढ़ाने पर समकोण पर मिलती हैं।
NA
Topper's Solved these Questions
- BOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8.27videos
चतुर्भुज
- BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - दीर्घ उत्तरीय प्रश्न5videos
समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
- BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )8videos
त्रिभुज
Similar Questions
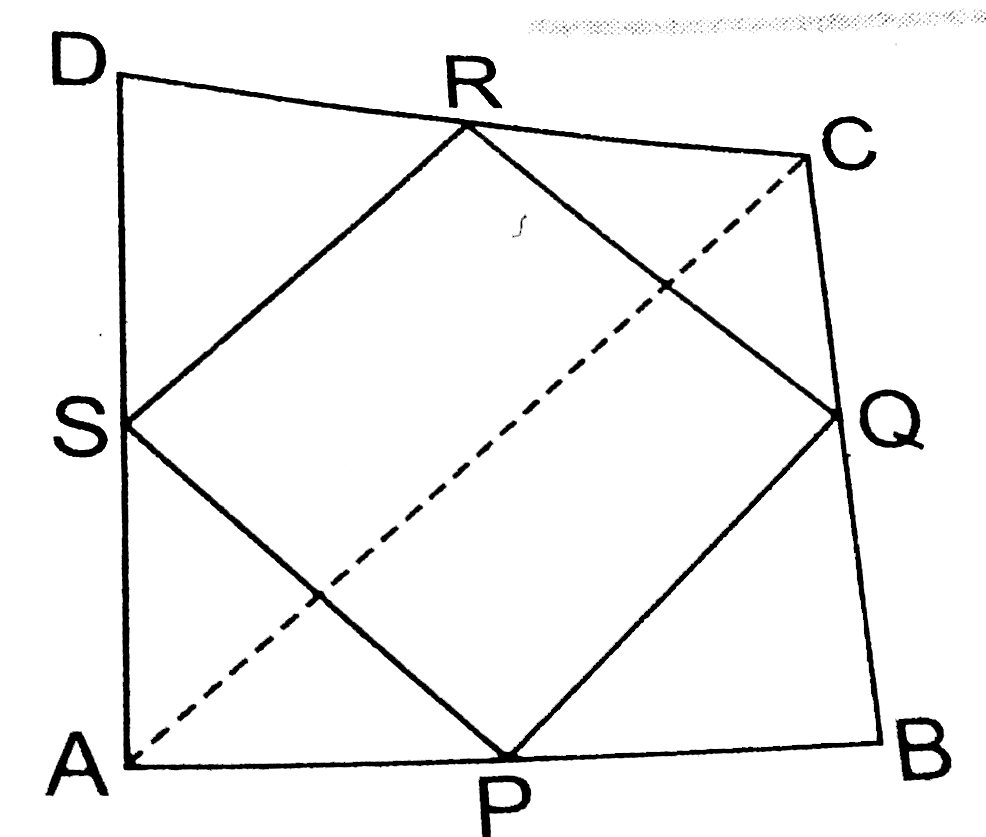
ABCD एक चतुर्भुज है जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य बिंदु हैं । AC उसका एक विकर्ण है। दर्शाइए कि:
(i) SR∣∣AC और SR=12AC है।
(ii) PQ=SR है।
(iii) PQRS एक समांतर चतुर्भुज है।
 05:52View Solution
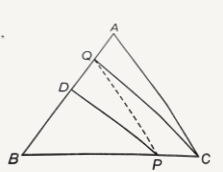
05:52View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
 02:34View Solution
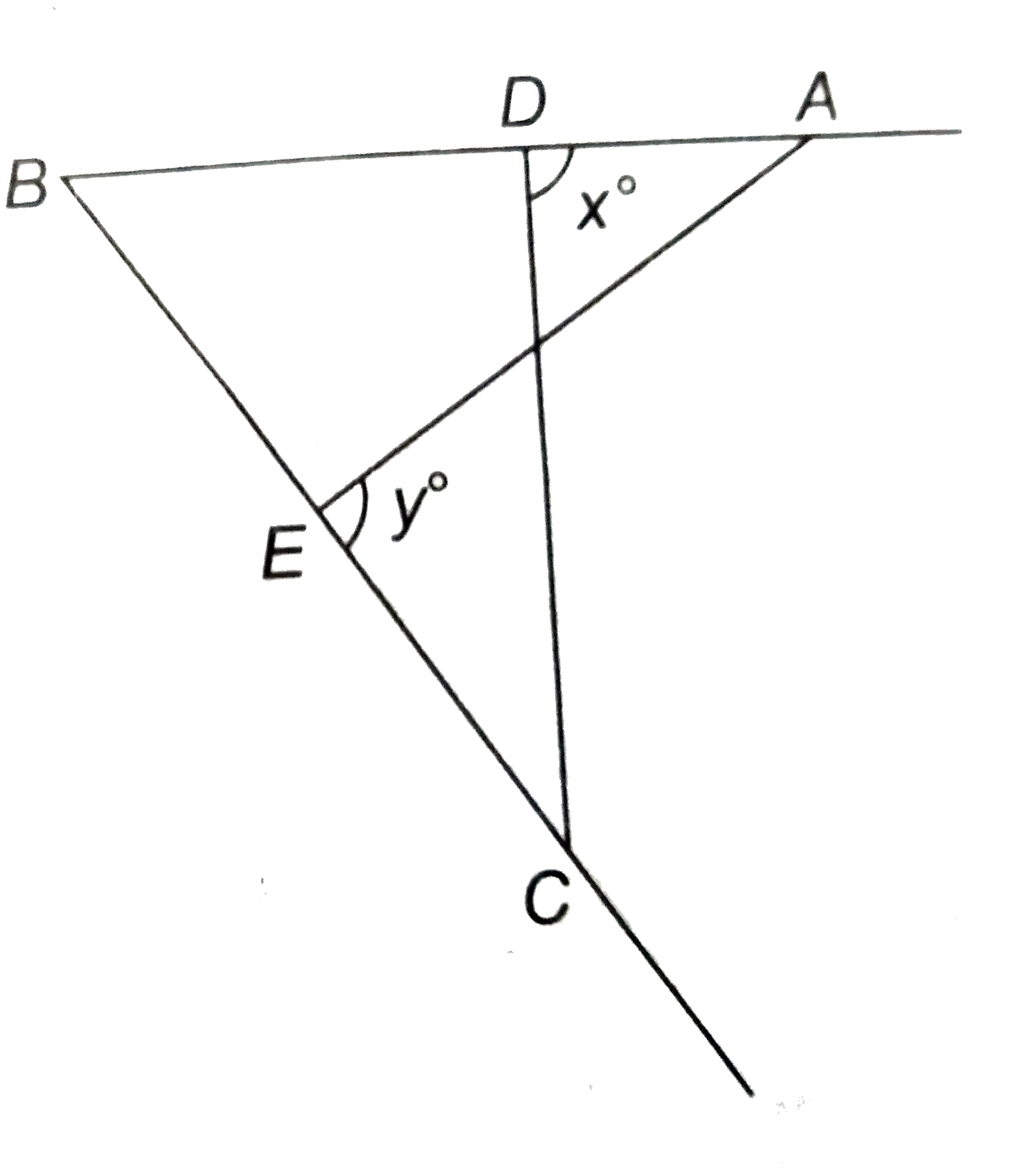
02:34View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
 04:48View Solution
04:48View SolutionABCD is a rhombus. RABS is a straight line such that RA = AB = BS. Prove that RD and SC when produced meet at right angles.
03:29View Solutionयदि ¯a और ¯b दो सदिश इस प्रकार हैं कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b लंबवत होगा b पर ।
03:54View Solutionएक सरल रेखा , अक्षो के साथ ऐसा समकोण त्रिभुज बनातीं है कि जिसके कर्ण कि लम्बाई √53 तथा क्षेत्रफल 7 वर्ग इकाई है । रेखा का समीकरण ज्ञात कीजिए
03:21View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
02:50View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
06:04View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
02:42View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
02:09View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
02:53View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
03:18View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
02:56View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
04:14View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
05:05View Solution

