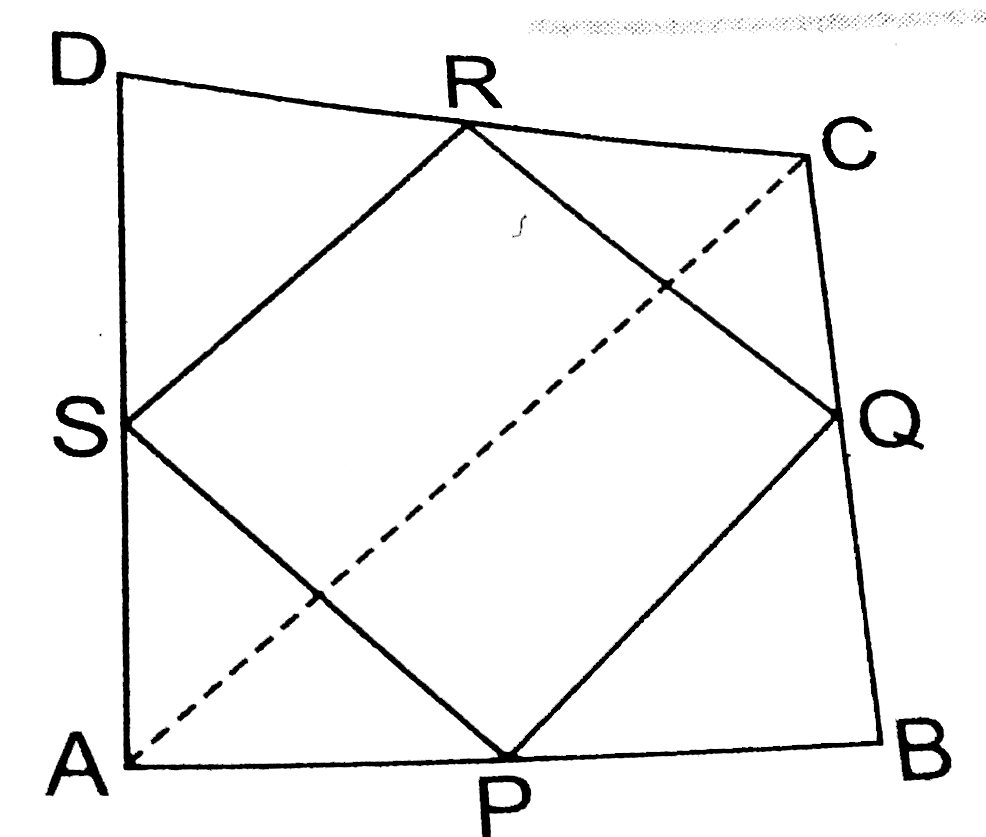
ABCD एक समचतुर्भुज है। RABS एक सरल रेखा इस प्रकार है कि RA=AB=BS है । सिद्ध कीजिए कि RD और SC बढ़ाने पर समकोण पर मिलती हैं।
NA
Topper's Solved these Questions
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - प्रश्नावली 8.2
7 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - दीर्घ उत्तरीय प्रश्न
5 Videos
- त्रिभुज BOOK - NOOTAN HINDICHAPTER - त्रिभुज EXERCISE - विविधि प्रश्नावली ( दीर्घ उत्तरीय प्रश्न )
8 Videos
Similar Questions
ABCD एक चतुर्भुज है जिसमें P,Q,R और S क्रमशः भुजाओं AB,BC,CD और DA के मध्य बिंदु हैं । AC उसका एक विकर्ण है। दर्शाइए कि:
(i) SR∣∣AC और SR=12AC है।
(ii) PQ=SR है।
(iii) PQRS एक समांतर चतुर्भुज है।
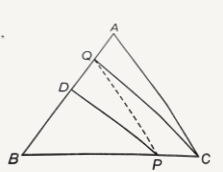
View Solutionसंलग्न चित्र में, ΔABC में AB का मध्य-बिन्दु D है तथा BC पर कोई बिन्दु P है। यदि CQ || PD, AB को Q पर मिलती है, तो सिद्ध कीजिए कि ar(ΔBPQ)=12ar(ΔABC)
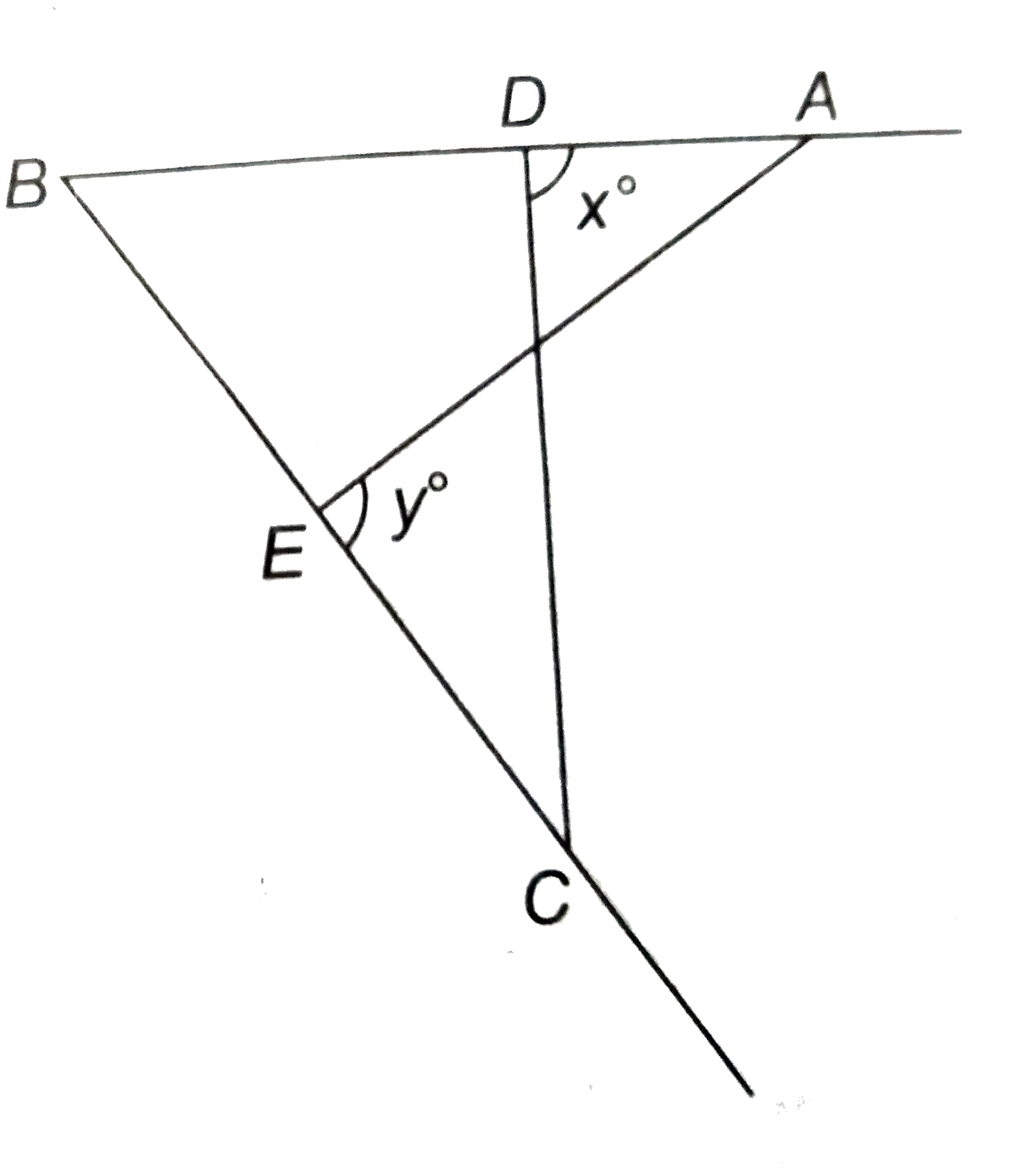
View Solutionदी आकृति में, यदि x = y और AB = CB है, तो सिद्ध कीजिए कि AE = CD है।
View SolutionABCD is a rhombus. RABS is a straight line such that RA = AB = BS. Prove that RD and SC when produced meet at right angles.
View Solutionयदि ¯a और ¯b दो सदिश इस प्रकार हैं कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b लंबवत होगा b पर ।
View Solutionएक सरल रेखा , अक्षो के साथ ऐसा समकोण त्रिभुज बनातीं है कि जिसके कर्ण कि लम्बाई √53 तथा क्षेत्रफल 7 वर्ग इकाई है । रेखा का समीकरण ज्ञात कीजिए
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View Solutionयदि ¯a,¯b दो सदिश इस प्रकार है कि ∣∣¯a+¯b∣∣=|¯a|, तो सिद्ध कीजिए कि 2¯a+¯b सदिश ¯b पर लम्ब है |
View Solutionयदि दो सदिश ¯a और ¯b इस प्रकार हैं कि ∣∣¯a+¯b∣∣=∣∣¯b∣∣, तब सिद्ध कीजिए कि ¯a+2¯b, सदिश ¯a पर लम्ब है |
View Solutionसिद्ध कीजिए कि फलन f(x)=|x|,x=0 पर अवकलनीय नहीं है यद्यपि यह x=0 पर संतत है|
View Solutionयदि परिमेय संख्याओं के समुच्चय Q पर संक्रिया (∗) इस प्रकार परिभाषित है कि a∗b=2a+3b . दिखाइए कि (∗) समुच्चय Q पर एक द्विआधारी संक्रिया है।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solutionएक गोले कि त्रिज्या 7 सेमी. मापी जाती है जिसमे 0.02 सेमी. कि त्रुटि है। इस त्रुटि के कारण इसके आयतन कि गणना में सनिकटन त्रुटि ज्ञात कीजिए।
View Solutionएक समतल निर्देशांकों अक्षों को A,B,C पर इस प्रकार मिलता है कि त्रिभुज ABC का केंद्रक (1,2,3) है तो समतल का समीकरण होगा
View Solution
