दर्शाइए कि समान्तर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाटते है।
हम जानते है कि समान्तर चतुर्भुज का विकर्ण इसे दो बराबर क्षेत्रफल के त्रिभुजों में विभाजित करता है।
समान्तर में,

AC इसका विकर्ण है।
का क्षेत्रफल का क्षेत्रफल का क्षेत्रफल
हम जानते है कि समान्तर चतुर्भुज के विकर्ण एक-दूसरे को समद्विभाजित करते है।
AO = OC
D से AC पर लम्ब DM है।
का क्षेत्रफल
का क्षेत्रफल
का क्षेत्रफल = का क्षेत्रफल
का क्षेत्रफल
का क्षेत्रफल
का क्षेत्रफल
इसी प्रकार सिद्ध कर सकते है कि
का क्षेत्रफल
का क्षेत्रफल
का क्षेत्रफल
का क्षेत्रफल का क्षेत्रफल
समान्तर चतुर्भुज के विकर्ण इसे बराबर क्षेत्रफल के चार त्रिभुजों में विभाजित करते है।
Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 9.4
Explore 8 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:अतिलघु उत्तरीय प्रश्न
Explore 10 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:NOOTAN HINDIChapter: समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 9.2
Explore 6 Videos
- चतुर्भुजBook:NOOTAN HINDIChapter:चतुर्भुजExercise:विविध प्रश्नावली
Explore 24 Videos
Similar Questions
समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत्रफल बराबर है। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप आयत के परिमाप से अधिक है।
View Solutionएक समचतुर्भुज के विकर्णों की लम्बाईयाँ 12 सेमी और 16 सेमी है। समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionआकृति में, ABCD एक समान्तर चतुर्भुज है, AE⊥DC और CF⊥AD है। यदि AB = 16 cm, AE = 8 cm और CF = 10 cm है, तो AD ज्ञात कीजिए।
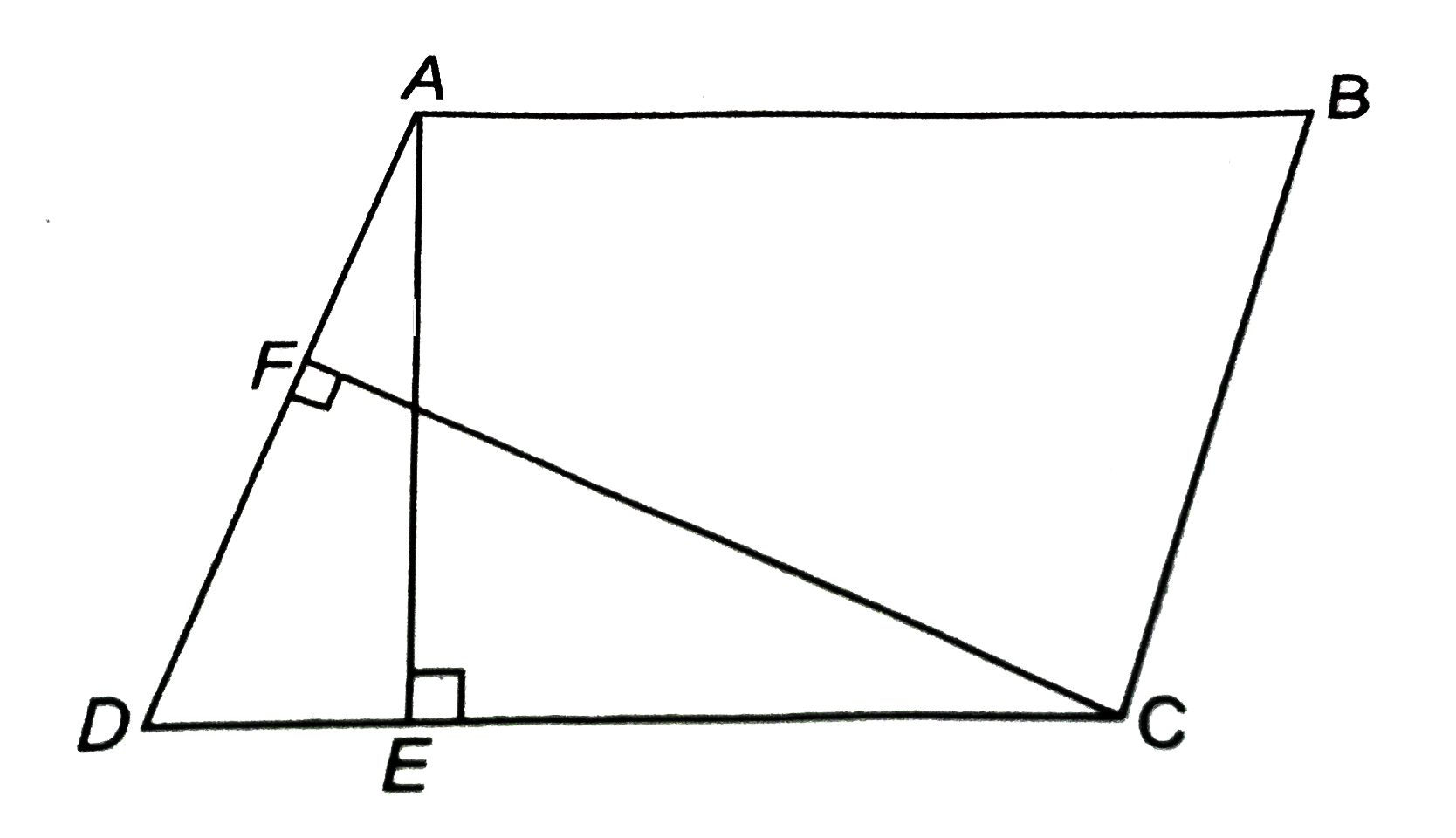
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solutionयदि समान्तर चतुर्भुज कि दो आसान भुजाएँ →a तथा →b हो , तो इसका विकर्ण ज्ञात कीजिए।
View Solutionएक समान्तर चतुर्भुज की दो आसान भुजाएँ 2ˆi−4ˆj−5ˆk और 2ˆi+2ˆj+3ˆk है । इसके दोनों विकणों के समान्तर दो मात्रक सदिश ज्ञात कीजिए। विकणों के सदिशों का प्रयोग करके समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
View Solutionदर्शाइए कि चार बिंदु A,B,C तथा D जिनके स्थिति सदिश क्रमश:: 4ˆi+5ˆj+ˆk,−ˆj−ˆk,3ˆi+9ˆj+4ˆk तथा 4(−ˆi+ˆj+ˆk) है , समतलीय है।
View Solution1 से 11 तक के पूर्णांकों में से यादृच्छया दो पूर्णांकों को चुना गया है | दोनों पूर्णांकों के विषय होने कि प्रायिकता ज्ञात करो यदि यह ज्ञात है कि दोनों पूर्णांकों का योग सम है |
View Solutionयदि p,q,r,s,t तथा u समान्तर श्रेणी (AP) में हैं, तो अन्तर (t- r) बराबर है
View Solutionयदि दो समरूप त्रिभुजों की भुजाओं का अनुपात 3:5 है, तो उनके क्षेत्रफलों का अनुपात है :
View Solutionदो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात 5:3 है, तो उनके संगत भुजाओं का अनुपात है :
View Solutionदर्शाइए कि धनात्मक सम पूर्णांक 4q या 4q+2 के रूप का होता है, जहाँ एक पूर्णाक है।
View Solutionसमान्तर चतुर्भुज के प्रश्नो को हल करना सीखे
View SolutionRevision|चतुर्भुज#!#चतुर्भुज के प्रकार#!#समान्तर चतुर्भुज
View SolutionA solid cube of volume 13824cm3 is cut into 8 cubes of equal volumes. The ratio of the surface area of the original cube to the sum of the surface areas of three of the smaller cubes is :
13824 घन सेमी आयतन वाले एक ठोस घन को बराबर आयतन वाले आठ घनों में काटा जाता है| आरंभिक घन के पृष्ठ क्षेत्रफल तथा तीन छोटे घनों के पृष्ठ क्षेत्रफलों के योग का अनुपात क्या है ?
View Solutionजो शब्दांश किस शब्द के अंत में जुड़कर नया शब्द बनाते है उसे कहते है
View Solution
