आकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज है। यदि रेखाखण्ड CD रेखाखण्ड AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि ar(ABC) = ar (ABD) है।
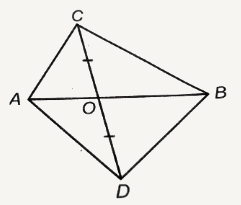
दिया है कि दो त्रिभुज ABC और ABD समान आधार AB पर है। रेखाखण्ड CD, AB को O पर समद्विभाजित करता है। (∵OC=OD)
ΔACD में,
OC = OD (दिया है)
∴AO माध्यिका है।
∵ माध्यिका एक त्रिभुज को बराबर क्षेत्रफलों के दो त्रिभुजों में विभाजित करती है।
∴ar(ΔAOC)=ar(ΔAOD) ...(1)
इसी प्रकार,
ΔBCD में, ar(ΔBOC)=ar(ΔBOD) ...(2)
समीकरण (1) और (2) को जोड़ने पर
ar(ΔAOC)+ar(ΔBOC)=ar(ΔAOD)+ar(ΔBOD)
⇒ar(ΔABC)=ar(ABD)
Topper's Solved these Questions
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.4
8 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - अतिलघु उत्तरीय प्रश्न
10 Videos
- समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - NOOTAN HINDICHAPTER - समान्तर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - प्रश्नावली 9.2
6 Videos
- चतुर्भुजBOOK - NOOTAN HINDICHAPTER - चतुर्भुजEXERCISE - विविध प्रश्नावली
24 Videos
Similar Questions
समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित है और उनके क्षेत्रफल बराबर है। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप आयत के परिमाप से अधिक है।
View Solutionएक समचतुर्भुज के विकर्णों की लम्बाईयाँ 12 सेमी और 16 सेमी है। समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
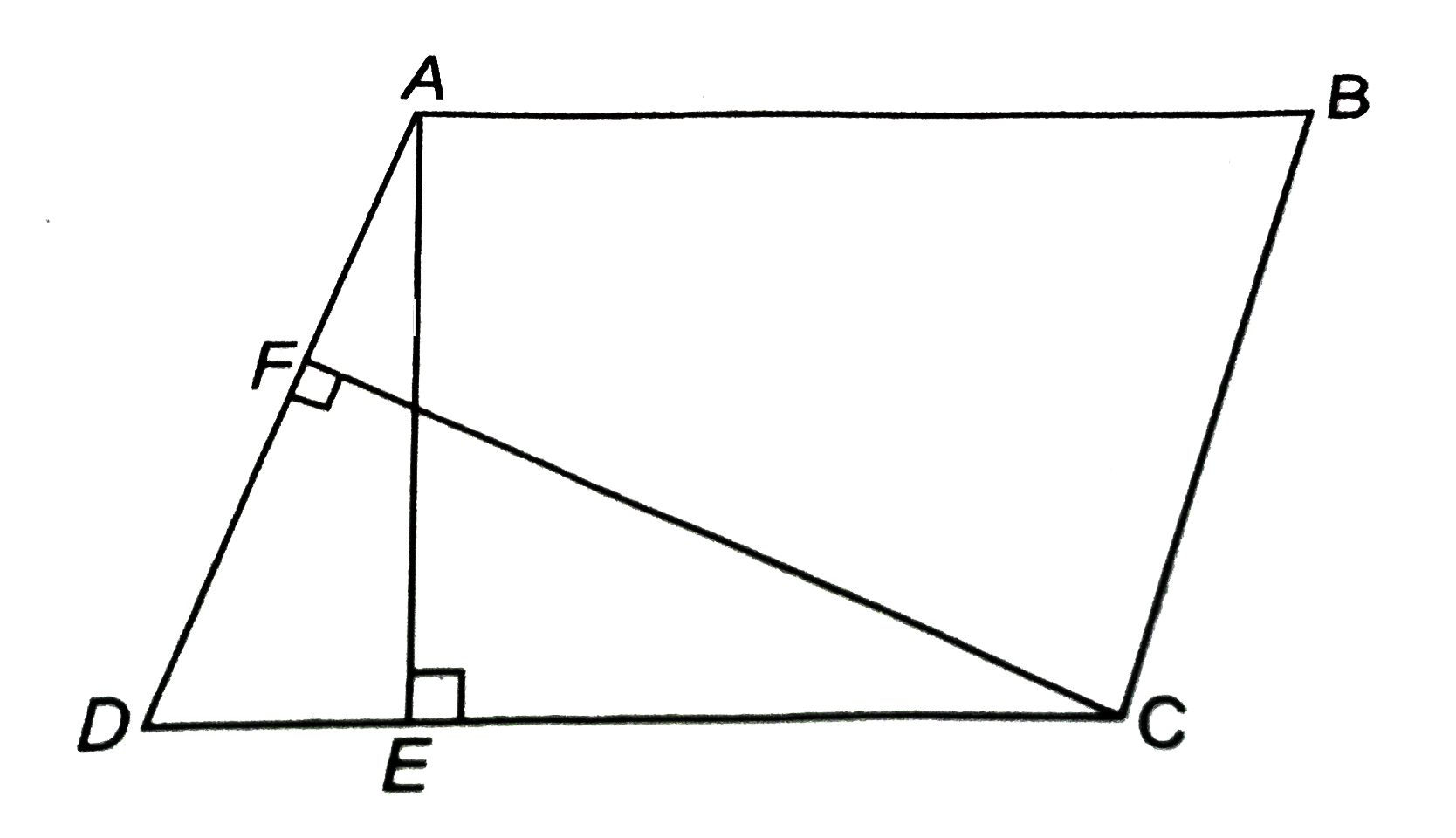
View Solutionआकृति में, ABCD एक समान्तर चतुर्भुज है, AE⊥DC और CF⊥AD है। यदि AB = 16 cm, AE = 8 cm और CF = 10 cm है, तो AD ज्ञात कीजिए।
View Solutionएक चतुर्भुज के तीन कोण 100∘,98∘,92∘ है। चौथा कोण ज्ञात कीजिए।
View Solution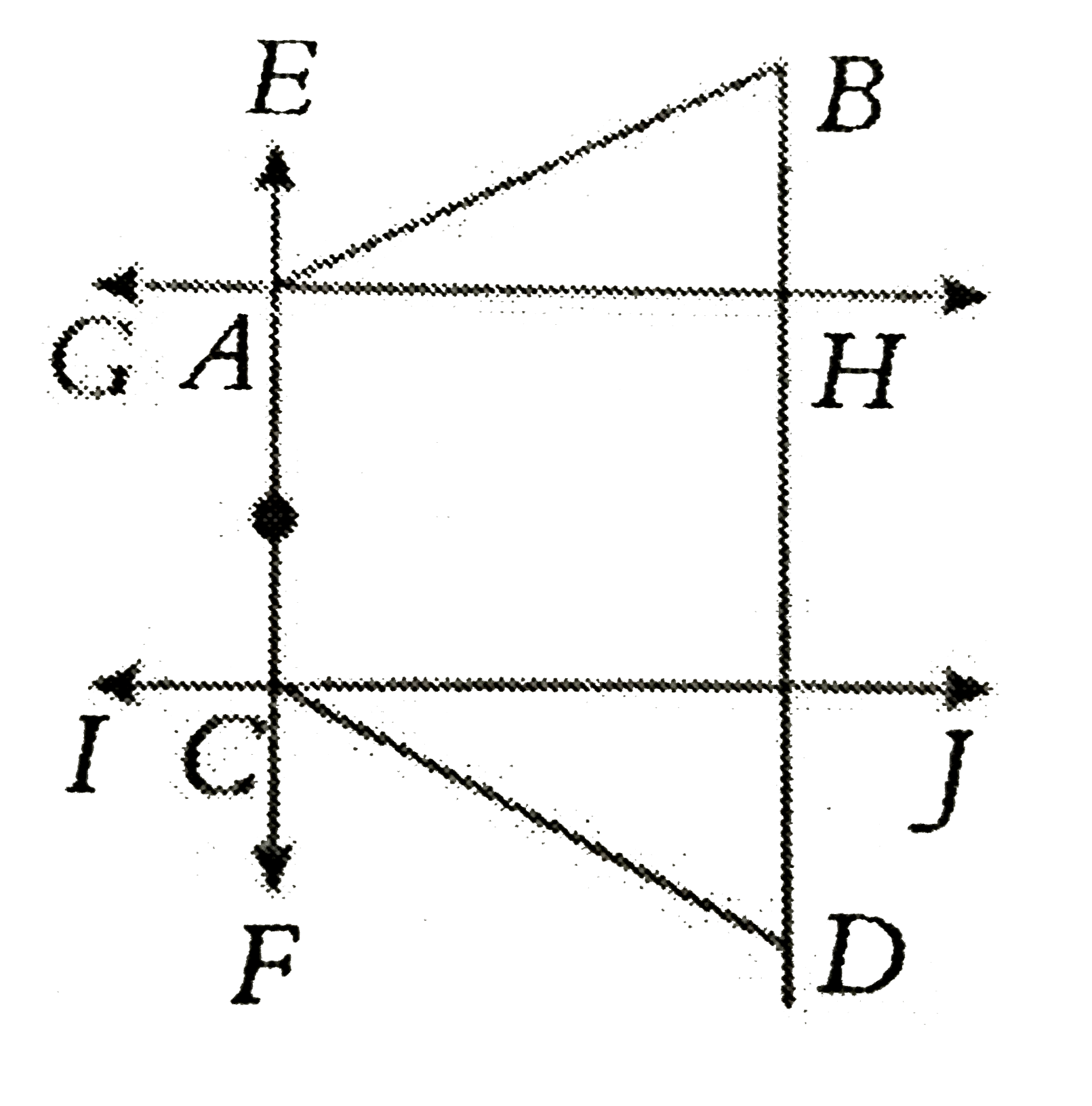
In the above figure, GH∣∣IJ and AC∣∣BD,AB and CD are bisectors of ∠EAH and ∠FCJ respectively. Find the ∠ABD+∠BDC, if ∠BAC=3∠BDC.
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionIn the figure above (not to scale), ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯CDandAD is the bisector of ∠BAE.AB=3cm and AC=5cm. Find CD.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
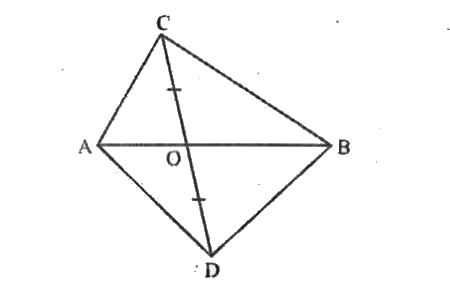
View SolutionIn, ABC and ABD are two triangles on the same base AB. If line- segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
View Solutionयदि बिंदु A(a,0) और B(−a,0) दो स्थिर बिंदु हों तो उस बिंदु का बिन्दुपथ ज्ञात कीजिए जिस पर रेखाखण्ड AB सदैव समकोण बनाता है ।
View SolutionIn the given figure, ABC and ABD are two triangles on the same base AB . If line - segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD)
View Solution
