एक पारद लैंप, प्रकाश-विद्युत उत्सर्जन की आवृत्ति निर्भरता के अध्ययन के लिए एक सुविधाजनक स्रोत है, क्योकिं यह दृश्य-स्पेक्ट्रम के पराबैगनी (UV) से लाल छोर तक कई-वर्ण रेखाएँ उत्सर्जित करता है। रूबीडियम प्रकाश सेल के हमारे प्रयोग में, पारद (Mercury) स्रोत की निम्न वर्ण-रेखाओं का प्रयोग किया गया :
λ1=3650Å,λ2=4047+Å,λ3=4358Å,λ4=5461Å,λ5=6907Å
निरोधी वोल्टताएँ, क्रमशः निम्न मापी गई :
V01=1⋅28V,V2=0⋅95V,V03=0⋅74V,V04=0⋅16V,V05=0V
प्लैंक स्थिरांक h का मान ज्ञात कीजिए।
[ नोट : उपयुर्क्त आँकड़ों से h का मान ज्ञात करने के लिए आपको e=1.6x10−19C की आवश्यकता होगी। इस प्रकार के प्रयोग Na,Li,K आदि के लिए मिलिकन ने किए थे। मिलिकन ने अपने तेल-बूँद प्रयोग से प्राप्त e के मान का उपयोग कर आइंस्टाइन के प्रकाश-विद्युत समीकरण को सत्यापित किया तथा इन्ही प्रेक्षणों से h के मान के लिए पृथक अनुमान लगाया। ]
दिया है -
λ1=3650Å=3650×1010m
⇒υe=cλ1=3×1083650×10−10=8⋅2×1014Hz
λ2=4047Å=4047×10−10m
⇒υe2=3×1084047×10−10=7⋅4×1014Hz
λ3=4358Å=4358×10−10m
⇒υe3=3×1084358×10−10=6⋅9×1014Hz
λ4=5461Å=5461×10−10Hz
⇒υe4=3×1085461×10−10=5⋅5×1014Hz
λ5=6907Å=6907×10−10m
⇒υe5=3×1086907×10−10=4⋅3×1014Hz
सांगत निरोधी वोल्टाएं है -
V01=1⋅28V,V02=0⋅95V,V03=0⋅74:V04=0⋅16V,V05=0V
निरोधी विभव V0 और आवृत्ति υe के बिच ग्राफ खींचे। पहली चार आवृत्तियों के सांगत बिंदु लगभग एक सरल रेखा पर स्थित है। यह रेखा υe−-अक्ष को 5×1014Hz पर काटती है। अतः देहली आवृत्ति υe=5×1014Hz पाँचवी आवृत्ति देहली आवृति से कम है। अतः इस आवृत्ति से प्रकाश-विद्युत उत्सर्जन संभव नहीं है जिससे निरोधी विभव शून्य होगा।
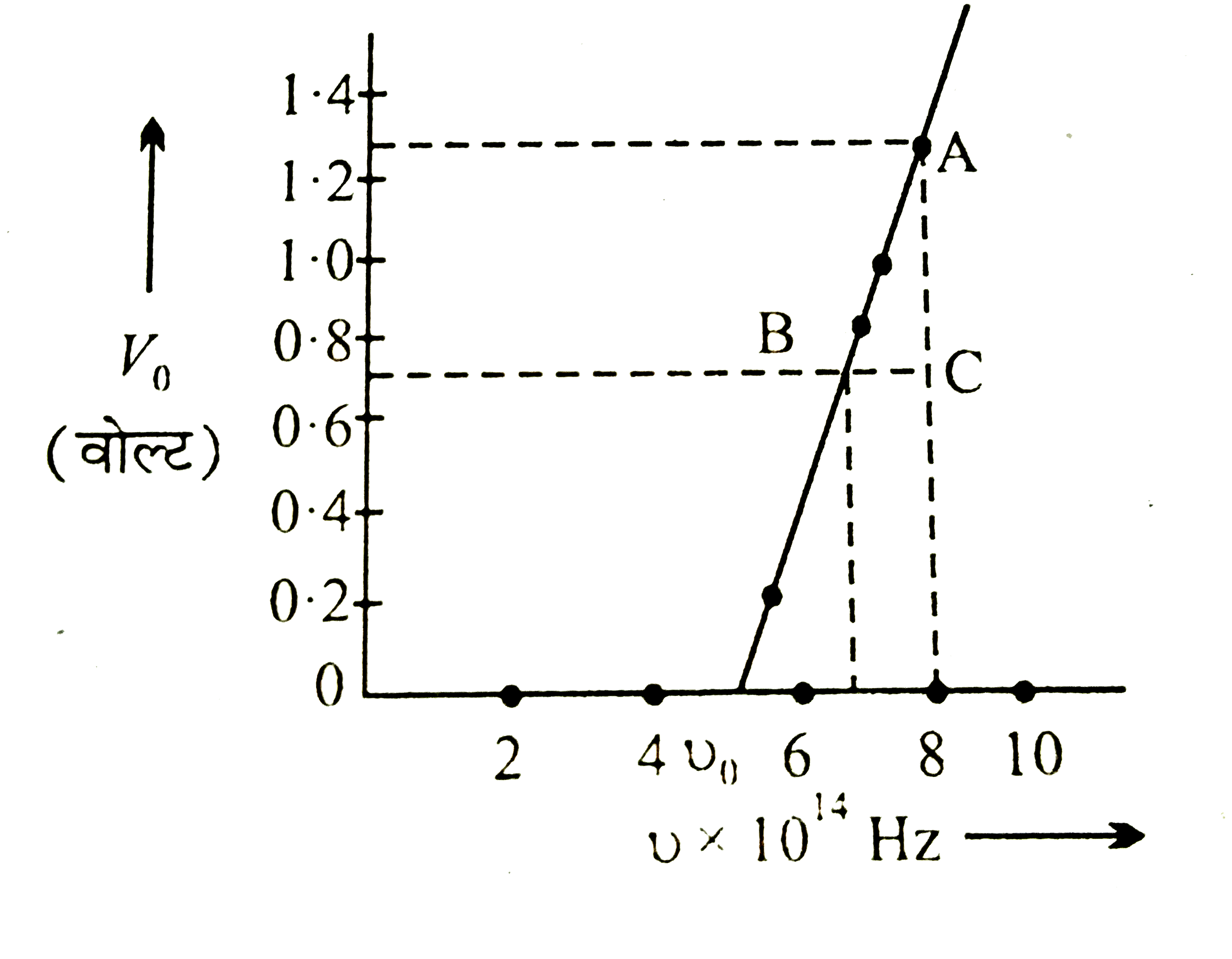
आइंस्टाइन के प्रकाश-विद्युत समीकरण से
eV0=hv−ϕ0
या V0=hev−ϕ0e
अतः he=V0−v की ढलान (Slope)
=ACBC=1⋅28−0⋅748⋅2×1014−69×1014
∴h==0⋅541⋅3×1014×e=0⋅54×10−141⋅3×1⋅6×10−19
=0⋅667×10−33
=6⋅67×10−33Js
=6⋅67×10−34Js
Similar Questions
बताएँ कि नीचे परिभाषित दो अनुपातों α और β में से कौन-सा एक से ज्यादा या एक से कम है।
α=vx−किरणेंvअवरक्त,β=λदृश्य प्रकाशλसूक्ष्मतरंग
View Solutionएक पारद लैंप, प्रकाश विद्युत उत्सर्जन की आवृत्ति निर्भरता के अध्ययन के लिए एक सुविधाजनक स्त्रोत है क्योंकि यह दृश्य –स्पेक्ट्रम के परबैंगनी (UV) के लाल छोर तक कइ वर्ण रेखाएं उत्सर्जित करता हैं रूबीडियम प्रकाश सेल के हमारे प्रयोग में पारद स्त्रोत की निम्न वर्ण रेखाओं का प्रयोग किया गया
λ1=3650Å,λ2=4047Å,λ3=4358Å,λ4=5461Å,λ5=6907Å,
निरोधी वोल्टताएं क्रमशः निम्न मापी गई
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V
(a) प्लैंक स्थिरांक h का मान ज्ञात कीजिए।
(b) धातु के लिए देहली आवृत्ति तथा कार्य फलन का आकलन कीजिए।
View SolutionCut off potential for a metal in photoclectric effect for light of wavelength lambda_(1), lambda_(2) and lambda_(3) is found to be V_(1),V_(2) and V_(3) volts , If V_(1),V_(2) and V_(3 are in Arithmetic progression then lambda_(1),lambda_(2) and lambda_(3) will be in
View SolutionThe wavelengths and frequencies of photons in transition 1,2 and 3 for hydrogen like atom are lambda_(1),lambda_(2),lambda_(3), v_(1),v_(2) and v_(3) respectively. Then:
View SolutionA mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the end of the red visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used: λ1=3650A∘,λ2=4047A∘,λ3=4358A∘,λ4=5461A∘,λ5=6907A∘ The stopping voltages, respectively were measured to be:
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V.
(a) Determine the value of Planck's constant h.
(b) Estimate the threshold frequency and work function for the material.
View SolutionA mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used:
λ1=3650Å,λ2=4047Å,λ3=4358Å,λ4=5461Å,λ5=6907Å
The stopping voltages respectively were measured to be
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0
Determine the value of Planck.s constant h, the threshold frequency and work function for the material.
View SolutionA mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used:
λ1=3650Å,λ2=4047Å,λ3=4358Å,λ4=5461Å,λ5=6907Å
The stopping voltages respectively were measured to be
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0
Determine the value of Planck.s constant h, the threshold frequency and work function for the material.
View SolutionCut off potential for a metal in photoclectric effect for light of wavelength lambda_(1), lambda_(2) and lambda_(3) is found to be V_(1),V_(2) and V_(3) volts , If V_(1),V_(2) and V_(3 are in Arithmetic progression then lambda_(1),lambda_(2) and lambda_(3) will be in
View Solution
