A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red end of the visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used:
λ1=3650Å,λ2=4047Å,λ3=4358Å,λ4=5461Å,λ5=6907Å
The stopping voltages respectively were measured to be
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0
Determine the value of Planck.s constant h, the threshold frequency and work function for the material.
Given, the following wavelength from a mercury source were used:
λ1=3650Å=3650×10−10m
λ2=4047Å=4047×10−10m
λ3=4358Å=4358×10−10m
λ4=5461Å=6907×10−10m
The stopping voltages are as follows:
V01=1.28V,V02=0.95V,
V03=0.74V
V04=0.16VandV05=0
Frequencies corresponding to wavelengths,
v1=cλ1=3×1083650×10−10=8.219×1014Hz
v2=cλ2=3×1084047×10−10=7.412×1014Hz
v3=cλ3=3×1084358×10−10=6.884×1014Hz
v4=cλ4=3×1085461×10−10=5.493×1014Hz
v5=cλ5=3×1086907×10−10=4.343×1014Hz
As we know that,
eV0=hv−ϕ0⇒V0=hve−ϕ0e
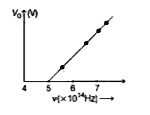
As the graph between V0 and frequency v is a straight line.
The slope of this graph gives the values of he.
∴he=V01−V04v1−v4=1.28−0.16(8.219−5.493)×1014=1.122.726×1014
h=1.12×1.6×10−192.726×1014=6.573×10−34J−s
Work function, ϕ0=hv0=6.573×10−34×5×1014
=32.865×10−20J=2.05eV
Similar Questions
A mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the red and end of the visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used:
λ1=3650Å,λ2=4047Å,λ3=4358Å,λ4=5461Å,λ5=6907Å
The stopping voltages, respectively, were measured to be:
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V
Determine the value of Planck's constant h, the threshold frequency and work function for the material.
View SolutionA mercury lamp is a convenient source for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the end of the red visible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used: λ1=3650A∘,λ2=4047A∘,λ3=4358A∘,λ4=5461A∘,λ5=6907A∘ The stopping voltages, respectively were measured to be:
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V.
(a) Determine the value of Planck's constant h.
(b) Estimate the threshold frequency and work function for the material.
View Solution
Knowledge Check
If λv,λmandλx represent wavlength of visible light, microwaves and X - rays respectively, then
Aλm<λx<λvBλv<λm<λxCλx<λv<λmDλm<λv<λxif λv',λx and λm represent the wavelengths of visible light X-rays and microwaves respectively then:
Aλm>λx>λvBλk>λm>λxCλm>λv>λxDλy>λx>λmThe ratio of resolving power of an optical microscope for two wavelength λ1=4000Å and λ2=6000Å is:
A9:4B3:2C16:81D8:27
A mercury lamp is a convenient souce for studying frequency dependence of photoelectric emission, since it gives a number of spectral lines ranging from the UV to the end of the red vissible spectrum. In our experiment with rubidium photocell, the following lines from a mercury source were used: λ1=3650A∘,λ2=4047A∘,λ3=4358A∘,λ4=5461A∘,λ5=6907A∘ The stopping voltages, respectively were measured to be:
V01=1.28V,V02=0.95V,V03=0.74V,V04=0.16V,V05=0V.
(a) Determine the value of Planck's constant h.
(b) Estimate the threshold frequency and work function for the material.
View SolutionThe ratio of resolving power of an optical microscope for two wavelength λ1=4000Å and λ2=6000Å is:
View SolutionThe wavelengths and frequencies of photons in transition 1,2 and 3 for hydrogen like atom are λ1,λ2,λ3,v1,v2 and v3 respectively. Then:

View SolutionThe wavelengths and frequencies of photons in transition 1,2 and 3 for hydrogen like atom are λ1,λ2,λ3,v1,v2 and v3 respectively. Then:

View SolutionThe ratio of resolving power of an optical microscope for two wavelength λ1=4000Å and λ2=6000Å is:
View Solution
