सत्य/असत्य बताइए तथा उत्तर का औचित्य भी बताइए -
ABC और BDE दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य-बिंदु है। तब
ar(BDE)=14ar(ABC).
The correct Answer is:सत्य
Step by step video, text & image solution for सत्य/असत्य बताइए तथा उत्तर का औचित्य भी बताइए - ABC और BDE दो समबाहु त्रिभुज इस प्रकार है की D भुजा BC का मध्य-बिंदु है। तब ar(BDE)=(1)/(4)ar(ABC). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - SHIVLAAL PUBLICATIONCHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - अति लघु उत्तरीय प्रश्न
3 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - SHIVLAAL PUBLICATIONCHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - लघु उत्तरीय प्रश्न
12 Videos
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल BOOK - SHIVLAAL PUBLICATIONCHAPTER - समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल EXERCISE - एक शब्द/वाक्य में उत्तर
4 Videos
- रेखाएँ और कोण BOOK - SHIVLAAL PUBLICATIONCHAPTER - रेखाएँ और कोण EXERCISE - दीर्घ उत्तरीय प्रश्न
4 Videos
- सांख्यिकी BOOK - SHIVLAAL PUBLICATIONCHAPTER - सांख्यिकी EXERCISE - लघु उत्तरीय प्रश्न
8 Videos
Similar Questions
किस समान्तर चतुर्भुज का आधार 20 सेमी तथा ऊँचाई (शीर्षलम्ब) 10 सेमी है, तो समान्तर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए की यदि दो समांतर चतुर्भुज एक ही आधार पर व समान्तर रेखाओं के एक ही युग्म के बीच स्थित हो, तो उनके क्षेत्रफल बराबर होते है।
View Solutionएक सरल बंद आकृति द्वारा घेरा गया तल क्या कहलाता है ?
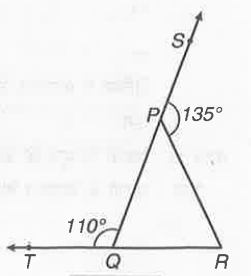
View Solutionसंलग्न चित्र में ΔPQR की भुजाओं QP और RQ को क्रमशः बिन्दुओं S और T तक बढ़ाया गया है। यदि ∠SPR=135∘ और ∠PQT=110∘ है, तो ∠PRQ ज्ञात कीजिए।
View Solutionआठवीं कक्षा के 30 विधार्थियो के रक्त समूह ये हैं :
A,B,O,O,AB,O,A,O,B,A,O,B,A,O,O,A,AB,O,A,A,O,O,AB,B,A,O,B,A,B,O.
इन आँकड़ो को एक बारम्बारता बंटन सारणी के रूप में प्रस्तुत कीजिए । बताइए की इन विधार्थियो में कौन सा रक्त समूह अधिक समान्य है और कौन-सा रक्त समूह विरलतम रक्त समूह है ?
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
View SolutionIn the following figure , ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar (BDE) = 14 ar (ABC)
(ii) ar (BDE) = 12 ar (BAE)
(iii) ar (ABC)= 2 ar (BEC)
(iv) ar (BFE) = ar (AFD)
(v) ar (BFE) = 2 ar (FED)
(vi) ar (FED) = 18 ar(AFC)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=14ar(ΔABC).
View SolutionIn fig, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that: (i) ar(BDE)= 1/4 ar(ABC) (ii) ar(BDE)= 1/2 ar(BAE)
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then ar (BDE)=14 ar(ABC).
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. If the area of triangle ABC is 136 cm^2 , then the area of triangle BDE is equal to: ABC और BDE दो समबाहु त्रिभुज हैं जेसे D, BC का मध्य-बिंदु है। यदि त्रिभुज ABC का क्षेत्रफल 136 cm^2 , है, तो त्रिभुज BDE का क्षेत्रफल ज्ञात करे
View SolutionIn triangle ABC , D is a point on side AB, such that, BD = 2cm and DA = 3cm. E is a point on BC such that DE || AC and AC = 4 cm. Then (Area of triangle BDE ): (Area of trapezium ACED) is: त्रिभुज ABC में, D, भुजा AB पर स्थित ऐसा बिंदु है कि BD = 2 सेमी और DA =3 सेमी है | E, BC पर स्थित ऐसा बिंदु है कि DE || AC है और AC =4 सेमी है | तो त्रिभुज (BDE का क्षेत्रफल ) : (समलम्ब ACED का क्षेत्रफल) ज्ञात करें |
View SolutionIn triangle ABC ,P is a point on BC such that BP : PC = 1 : 2 and Q is the mid point of BP. then, ar(triangle ABQ) :ar (triangle ABC) is equal to: त्रिभुज ABC में, P, BC पर स्थित ऐसा बिंदु है कि BP : PC = 1 : 2 है और Q, BP का मध्य बिंदु है | तो ar(triangle ABQ) :ar (triangle ABC) का मान क्या होगा ?
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 3 : 4 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ABC) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 3 : 4 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ABC) का मान ज्ञात करें |
View SolutionIn △ABC ,P is a point on BC such that BP : PC = 4 : 3 and Q is the midpoint of BP. Then ar(△ABQ):ar(△ACB) is equal to:
त्रिभुज ABC में, P, BC पर स्थित एक ऐसा बिंदु है कि BP : PC = 4 : 3 है और Q, BP का मध्य बिंदु है | ar(△ABQ):ar(△ACB) का मान ज्ञात करें |
View Solution