In fig, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that: (i) ar(BDE)= 1/4 ar(ABC) (ii) ar(BDE)= 1/2 ar(BAE)
Step by step video & image solution for In fig, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that: (i) ar(BDE)= 1/4 ar(ABC) (ii) ar(BDE)= 1/2 ar(BAE) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=14ar(ΔABC).
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC in F. Prove that: ar(△BFE)=2ar(△FED).
View SolutionABC and BDE are two equilateral triangles such that D is the mid- point of BC. If AB = 20 cm . Find the area of the shaded portions [ Take √3=1.73]
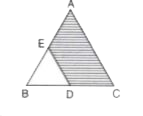
View SolutionTick the correct answer and justify:ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2:1 (B) 1:2 (C) 4:1 (D) 1:4
View SolutionIf the median of a △ABC intersect at G. show that ar (△AGC) = ar (△AGB) = ar (△BGC) = 1/3 ar (△ABC)
View SolutionIn Fig. 3, ABC is a right triangle, right angled at C and D is the mid-point of BC. Prove that AB2=4AD2−3AC2.
View SolutionIn an equilateral triangle ABC , D is the mid-point of AB and E is the mid-point of AC. Find the ratio between ar (△ABC):ar(△ADE)
View SolutionIn a triangle ABC,D is the mid - point of BC, AD is produced upto E so that DE = AD.
Prove that :
AB=EC
View SolutionIn a triangle ABC,B=90∘ and D is the mid-oint of BC then prove that AC2=AD2+3CD2
View SolutionThe given figure shows an equilateral triangles ABC and D is point in AC.
Prove that :
(i) AD<BD
(ii)BC>BD
View Solution
