द्रव्यमान m का एक पिण्ड, एकसमान द्रव्यमान M तथा बल नियतांक K की एक स्प्रिंग से लटका है | सिद्ध कीजिए कि दोलन आवृति n=12π√Km+(M/3) होगी |
माना चित्र 15.34 में स्प्रिंग की लम्बाई l है तो स्प्रिंग का प्रति एकांक लम्बाई द्रव्यमान =Ml
अब यदि ऊपर के दृढ़ सिरे से s दूरी पर लम्बाई ds की स्प्रिंग पर विचार करें तो
स्प्रिंग के इस भाग का द्रव्यमान =Mlds
माना स्प्रिंग के निचले सिरे पर जुड़े द्रव्यमान m को माध्य स्थिति से नीचे की और x दूरी विस्थापित किया जाता है तो चूँकि लम्बाई में वृद्धि ∝ प्रारम्भिक लम्बाई अतः ds लम्बाई वाले भाग का ऊर्ध्वाधर विस्थापन sxl होगा |
∴ भाग ds का वेग =s dxl dt=slv, जहाँ =dxdt स्प्रिंग के निचले सिरे पर द्रव्यमान m का वेग है।
 तथा द्रव्यमान m की गतिज ऊर्जा =12mv2
तथा द्रव्यमान m की गतिज ऊर्जा =12mv2
अतः स्प्रिंग से लटके सम्पूर्ण निकाय की कुल गतिज ऊर्जा
=12mv2+Mv26=v22(m+M3) br> =12(m+M3)(dxdt)2 .....(i)
तथा स्प्रिंग की स्थितिज ऊर्जा −∫x0Kx dx=12Kx3 ....(ii)
ऊर्जा संरक्षण के सिद्धांत से गतिज ऊर्जा + स्थितिज ऊर्जा = नियतांक
या 12(m+M3)(dxdt)2+12Kx2= नियतांक
t के सापेक्ष अवकलन करने पर, 12(m+M3)×2(dxdt)×d2xdt2+12K×2x×dxdt=0
या (m+M3)d2xdt2+Kx=0 या d2xdt2+K(m+M3)x=0
यह सरल आवर्त गति का अवकलन समीकरण है जिसकी कोणीय आवृत्ति ω=
⎷K(m+M3)
या आवृत्ति n=ω2π=12π
⎷K(m+M3)
Topper's Solved these Questions
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - दोलन EXERCISE - प्रश्न (वस्तुनिष्ठ प्रश्न )10videos
दोलन
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - दोलन EXERCISE - प्रश्न (सही जोड़ियाँ बनाइए - )2videos
दोलन
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - दोलन EXERCISE - वस्तुनिष्ठ प्रश्न79videos
दोलन
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - तरल के यान्त्रिक गुणEXERCISE - वस्तुनिष्ठ प्रश्न70videos
तरल के यान्त्रिक गुण
- BOOK - SHIVLAAL PUBLICATIONCHAPTER - द्रव्य के तापीय गुणEXERCISE - वस्तुनिष्ठ प्रश्न180videos
द्रव्य के तापीय गुण
Similar Questions
सरल आवर्त गति होती है :
04:10View Solutionसही जोड़ें
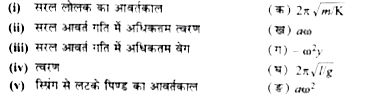 02:19View Solution
02:19View Solutionसरल आवर्त गति करते हुए एक कण के सम्बन्ध में असत्य कथन है :
06:35View Solutionगलत कथन है :
06:16View Solutionसेल्सियस स्केल पर परम शून्य की माप −273.15∘C है। फारेनहाइट स्केल पर परम शून्य की माप होगी :
07:02View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
08:04View Solutionm द्रव्यमान का इलेक्ट्रॉन (आवेश q ) एकसमान वैद्युत क्षेत्र E में विरामावस्था से त्वरित होता है। सिद्ध कीजिए कि x दूरी तय करने में इलेक्ट्रॉन द्वारा अर्जित वेग √2qExm होगा।
माना इलेक्ट्रॉन द्वारा x दूरी तय करने में अर्जित वेग v है, तब v2=02+2ax=2Fmx
परन्तु F=qE ∴V=√2qExm53:16View Solutionएक इलेक्ट्रॉन (द्रव्यमान किग्रा) व एक प्रोटॉन (द्रव्यमान किग्रा) के बीच गुरुत्वाकर्षण-बल व स्थिरवैघुत बल का अनुपात ज्ञात कीजिए। (e=1.6×10−19 कूलाम तथा G=6.67×10−11 (न्यूटन-मीटर^(2)/किग्रा^(2))
02:35View Solutionसिद्ध कीजिए कि सरल रेखाएँ x=mz+a,y=nz+b और x=m'z+a',y=n'z+b' एक-दूसरे को काटेंगी यदि (a−a')(n−n')=(b−b')(m−m') हो।
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionमाना कि k एक धनात्मक वास्तविक संख्या है तथा
A=⎡⎢ ⎢⎣2k−12√k2√k2√k1−2k−2√k2k−1⎤⎥ ⎥⎦ एवं B=⎡⎢ ⎢⎣02k−1√k1−2k02√k−√k−2√k0⎤⎥ ⎥⎦
यदि det (adj + A) + det (adj B) = 106, तो [k] का मान है।
[नोट adj M किसी वर्ग आव्यूह M का adjoint तथा [k] अधिकतम पूर्णांक जो k से कम या समान है। ]View Solutionबल तथा बल के प्रकार || जड़त्व, द्रव्यमान तथा भार || अरस्तू की भ्रामकता
View SolutionThe area of an equilateral triangle is 9 sqrt3 m^2 . The length (in m) of the median is- एक समबाहु त्रिभुज का क्षेत्रफल 9 sqrt3 m^2 है। तृदनुसार,उसको माध्यिका की लम्बाई कितने मीटर होगी?
View SolutionA bullet of mass 'm' and velocity 'a' is fired in to a large block of wood of mass 'm'. The final velocity of the system is द्रव्यमान 'm' और वेग '' की एक गोली द्रव्यमान 'm' के लकड़ी के बड़े ब्लॉक में दागी जाती है। सिस्टम का अन्तिम वेग क्या होगा?
View Solution1.0 mg के द्रव्यमान वाले एक कण का वेग 3600 km/h है। कण के तरंग दैर्ध्य की गणना कीजिए।
View Solutionवेग में अनिश्चितता की गणना कीजिए, यदि 10 ग्राम द्रव्यमान वाली एक गतिमान गोली की स्थिति में अनिश्चितता 10^(-5) m है।
View Solution

