चित्र 15.35 में एकसमान अनुप्रस्थ परिच्छेद की एक ऊर्ध्वाधर नली U में कोई द्रव इस प्रकार भरा है कि इसकी प्रत्येक भुजा में द्रव की ऊँचाई h है | यदि एक भुजा के द्रव को थोड़ा नीचे विस्थापित करके छोड़ा जाता है तो यह सरल आवर्ती दोलन करने लगता है | सिद्ध कीजिए कि दोलनों का आवर्तकाल T=2π√hg होगा |
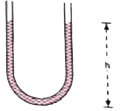
यदि एक भुजा में द्रव के तल को दूरी x नीचे विस्थापित करते है तो नली की दोनों भुजाओं में द्रव के तलो का अंतर 2x होगा द्रव पर प्रत्यानयन बल, ऊँचाई 2x के द्रव स्तम्भ के भार के बराबर होगा। तब संतुलन में, नली में द्रव का कुल भार =− प्रत्यानयन बल
यदि नली का अनुप्रस्थ परिच्छेद क्षेत्रफल A तथा द्रव का घनत्व ρ है तो
नली में द्रव का कुल भार = द्रव का आयतन × घनत्व × त्वरण =2hA×ρ×d2xdt2
तथा प्रत्यानयन बल = ऊँचाई 2x के द्रव स्तम्भ का भार =(2xA)×ρg
या d2xdt3=ghx अर्थात त्वरण ∝− विस्थापन
यह सरल आवर्त गति की शर्त है अतः सरल आवर्त गति का आवर्तकाल
T=3π√विस्थापनत्वरण=2π√hg
Topper's Solved these Questions
- दोलन BOOK - SHIVLAAL PUBLICATIONCHAPTER - दोलन EXERCISE - प्रश्न (वस्तुनिष्ठ प्रश्न )
10 Videos
- दोलन BOOK - SHIVLAAL PUBLICATIONCHAPTER - दोलन EXERCISE - प्रश्न (सही जोड़ियाँ बनाइए - )
2 Videos
- दोलन BOOK - SHIVLAAL PUBLICATIONCHAPTER - दोलन EXERCISE - वस्तुनिष्ठ प्रश्न
79 Videos
- तरल के यान्त्रिक गुणBOOK - SHIVLAAL PUBLICATIONCHAPTER - तरल के यान्त्रिक गुणEXERCISE - वस्तुनिष्ठ प्रश्न
70 Videos
- द्रव्य के तापीय गुणBOOK - SHIVLAAL PUBLICATIONCHAPTER - द्रव्य के तापीय गुणEXERCISE - वस्तुनिष्ठ प्रश्न
180 Videos
Similar Questions
सरल आवर्त गति होती है :
View Solutionसही जोड़ें
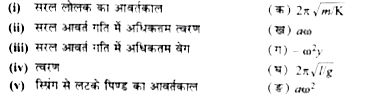
View Solutionसरल आवर्त गति करते हुए एक कण के सम्बन्ध में असत्य कथन है :
View Solutionगलत कथन है :
View Solutionसेल्सियस स्केल पर परम शून्य की माप −273.15∘C है। फारेनहाइट स्केल पर परम शून्य की माप होगी :
View Solutionठोस की द्रव में विलेयता, गैस की द्रव में विलेयता
View Solutionठोस पदार्थों की द्रव में विलेयता#!#द्रव में गैसों की घुलनशीलता#!#हेनरी का नियम
View SolutionIn a U-tube, the radii of the two pillars are respectively r_1 " और " r_2 Huh. When rho (theta = 0^@) घनत्व का एक द्रव इसमें भरा जाता है, तो दो भुजाओं के स्तर में h | का अंतर देखा जाता है। द्रव का पृष्ठ तनाव है:
View Solutionएक द्रव, जल में अमिश्रणीय है जो कि 0.983 atm के दाब और 95.2^(@)C पर भाप आसवित है। आसुत में जल के प्रति ग्राम में उपस्थित द्रव का द्रव्यमान क्या है। द्रव का मोलर द्रव्यमान 134.3 g/mol है और जल का वाष्प दाब 0.84 atm है। साथ ही, शुद्ध द्रव का वाष्प दाब 0.143 atm है।
View Solutionदो द्रवों A और B के एक आदर्श मिश्रण को पिस्टन युक्त एक सिलेण्डर में रखा जाता है। पिस्टन को समतापीय रूप से खीचने पर द्रव का आयतन घटता है लेकिन वाष्प का आयतन बढ़ जाता है। द्रव की बहुत छोटी मात्रा शेष बचती है और वाष्प में A का मोल प्रभाज 0.4 होता है। यदि प्रायोगिक ताप पर P_(A)^(@) = 0.4 और P_(B)^(@) = 1.2 atm है, तो निम्नलिखित में से किस कुल दाब पर द्रव लगभग वाष्पीकृत हो जाता है?
View SolutionNO_2 और N_2O_4 नाइट्रोजन डाइऑक्साइड के दो रूप हैं। एक गैसीय अवस्था में मौजूद होता है जबकि दूसरा द्रव अवस्था में। NO_2 और N_2O_4 रूपों की प्रकृति है:
View Solution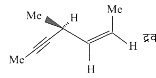
द्रव अमोनिया में सोडियम की उपस्थिति में उपरोक्त यौगिक का हाइड्रोजनीकरण देता है
View Solutionएक यौगिक M_p X_q में X की घनीय निविड़ संकुलन (ccp) व्यवस्था है। इसकी एकक कोष्ठिका की संरचना को नीचे दिखाया गया है। यौगिक का मूलानुपाती सूत्र है?
View Solutionयदि एक विशिष्ट विलायक में, एक यौगिक द्वारा समतल ध्रुवित प्रकाश का कोई घूर्णन नहीं होता है, यद्यपि यह किरैल है, तो इसका अर्थ हो सकता है कि
View Solutionशुद्ध द्रव A का वाष्प दाब, एक अवाष्पशील विलेय B को द्रव A में मिलाने पर 0.80 atm से 0.6 atm तक घट जाता है। विलयन में B का मोल प्रभाज है
View Solutionएक बंद ऊष्मारोधी पात्र में एक द्रव को इसके तापमान को बढ़ाने के लिए एक छड़ की सहायता से विडोलित किया जाता है। इस प्रक्रम में निम्नलिखित में से कौन सा सही है?
View Solution