सम्बन्ध p=αβe−αZkθ में p दाब, Z दूरी, k वोल्ट्जमान नियतांक तथा θ तापमान है। β का विमीय सूत्र होगा
[M0L2T0]
[ML2T]
[ML0T−1]
[M0L2T−1]
The correct Answer is:A
[αZkθ]=[M0L0T0]⇒[α]=[kθZ]
पुनः [p]=[αβ]
∴[β]=[αp]=[kθZp]
यहाँ, kθ की विमाएँ, ऊर्जा की विमाएँ है, अतः
[β]=[ML2T−2LML−1T−2]=[M0L2T0]
Topper's Solved these Questions
- सामान्य भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सामान्य भौतिकी EXERCISE - बहुविकल्पीय प्रश्न II
10 Videos
- सामान्य भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सामान्य भौतिकी EXERCISE - रिक्त स्थानों की पूर्ति कीजिए
4 Videos
- सरल आवर्त गति BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सरल आवर्त गति EXERCISE - विश्लेषणात्मक प्रश्न
8 Videos
- सॉल्वड पेपर (JEE MAIN 2019)BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सॉल्वड पेपर (JEE MAIN 2019)EXERCISE - 12 Jan, Shift-II (JANUARY ATTEMPT)
30 Videos
Similar Questions
L, C तथा R क्रमशः प्रेरकत्व, धारिता तथा प्रतिरोध को प्रकट करते है। निम्न में से कौन-से संयोग, आवृत्ति की विमा को व्यक्त करते है?
View Solutionप्लांक नियतांक की विमाएँ…………….है।
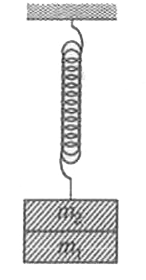
View Solutionदो द्रव्यमान m1 व m2 एक द्र्व्यमाणहीन स्प्रिंग से जिसका बल नियतांक k है , लटके हैं। जब दोनों द्रव्यमान साम्यावस्था में हैं, m1 को धीरे से हटा दिया जाता है। m2 के दोलन की कोणीय आवृत्ति तथा आयाम ज्ञात कीजिए ।
View Solutionएक m द्रव्यमान का अल्फ़ा कण किसी अज्ञात द्रव्यमान के स्थिर नाभिक से एक-विमीय प्रत्यास्थ संघट्ट करके अपनी प्रारम्भिक गतिज ऊर्जा का 64% भाग क्षय करके ठीक विपरीत दिशा में प्रकीर्णित हो जाता है। नाभिक का द्रव्यमान होगा
View SolutionPressure depends on distance as, P=αβexp(−αzkθ), where α,β are constants, z is distance as , k is Boltzman's constant and θ is tempreature. The dimension of beta are
View SolutionIn the relation P = (alpha)/(beta) e^(-alphaz//k theta),P is preesure, K is Botzmann's constant, Z is distance and theta is temperature. The dimensional formula of beta wll be
View SolutionIn the relation P = (alpha)/(beta) e^((alpha Z)/(k theta)) , P is pressure, Z is height, k is Boltzmann constant and theta is the temperature. Find the dimensions of alpha and beta
View SolutionIn the relation, P=alpha/beta e^((alphaZ)/(ktheta))P is pressure, Z is distance, k is Boltzmann constant and theta is the temperature. The dimensional formula of beta will be-
View Solutionp=(alpha)/(beta) exp (-(alphaz)/(K_(B))theta) theta rarr Temperature " " P rarr Pressure K_(B) rarr "Boltzman constant " Z rarr "Distance" Dimension of (alpha//beta) is -
View SolutionIn the relation: P=(alpha)/(beta)e^(-(alphaZ)/(ktheta)),P is pressure Z is distance k is Boltzmann constant and theta ils the temperature. The dimensional formula of beta will bes
View SolutionIn the releation p=αβe−azkθ, where p is the pressure z is distance k is Boltzmann constant and θ is the temperature the dimensional formula β will be
View Solutionदूरी z के साथ दाब P का विचरण, P=αβe−az/kθ से व्यक्त किया जाता है, जहाँ α,β नियतांक हैं, k बोल्ट्समान नियतांक तथा θ ताप है । β का विमीय सूत्र होगा :
View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
View SolutionIn the relation P=αβe−αz/kθ
where P=pressurez=distancek=Boltzman's constantθ=Temperature
The dimensional formula of β will be :
View SolutionPressure depends on distance as P=αβexp(−αzkθ) where αβ are constants z is distance k is Boltzmann is constant and θ is temperature. The dimension of β are
View SolutionIn the relation P=αβe−αzkθ is pressure, z is distance, k is Boltzmann constant and θ is the temperature. The dimensional formula of β will be
View Solution
