दूरी z के साथ दाब P का विचरण, P=αβe−az/kθ से व्यक्त किया जाता है, जहाँ α,β नियतांक हैं, k बोल्ट्समान नियतांक तथा θ ताप है । β का विमीय सूत्र होगा :
[M−1LT2]
[M0L0T0]
[M0L2T0]
[M−1L−1T−1]
The correct Answer is:C
घातांक αz/kθ विमाहीन राशि होगी, अर्थात
[αzkθ]=[m0L0T0].
∴[α]=[kθz]
अब, [P]=[αβ], क्योंकि घातांकी पद विमाहीन है ।
∴[β]=[αP]=[kθzP]
kθ कि विमये वही हैं जो PV की हैं (∵PV=kθ)
∴[β]=[PVzP]=[Vz]=[L3L]=[M0L2T0]
Topper's Solved these Questions
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - एन.सी.ई.आर.टी.प्रश्न
24 Videos
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - अतिरिक्त प्रश्न
9 Videos
- विमीय विश्लेषण BOOK - NOOTAN HINDICHAPTER - विमीय विश्लेषण EXERCISE - आंकिक
10 Videos
- मात्रक, मापन तथा त्रुटि विश्लेषण BOOK - NOOTAN HINDICHAPTER - मात्रक, मापन तथा त्रुटि विश्लेषण EXERCISE - विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न)
19 Videos
- वृत्तीय गति BOOK - NOOTAN HINDICHAPTER - वृत्तीय गति EXERCISE - अतिरिक्त प्रशन
17 Videos
Similar Questions
रिक्त स्थान भरिए :
(a) किसी 1 cm भुजा वाले घन का आयतन ...................m3 के बराबर है ।
(b) किसी 2 cm त्रिज्या व 10 cm ऊँचाई वाले सिलिंडर का पृष्ठ क्षेत्रफल...............(mm)2 के बराबर है ।
(c) कोई गाड़ी 18 km/h की चाल से चल रही है तो यह 1 s में ..............m चलती है ।
(d) सीसे का आपेक्षिक घनत्व 11.3 है । इसका घनत्व .......... g cm−3 या ................. kg m−3 है ।
View Solutionवर्षा के समय में कोई व्यक्ति चाल v के साथ तेजी से चला जा रहा है । उसे अपने छाते को टेढ़ा करके उर्ध्व के साथ θ कोण बनाना पड़ता है । कोई विद्यार्थी कोण θ व v के बीच निम्नलिखित संबंध व्युतपन्न करता है :
tanθ=v,
और वह इस संबंध के औचित्य की सिमा पता लगाता है, जैसी की आशा की जाती है यदि v → 0 तो θ→0 | (हम यह मान रहे हैं की तेज हवा नहीं चल रही है और किसी खड़े व्यक्ति के लिए वर्षा उर्ध्वाधरत: पद रही है) । क्या आप सोचते हैं की यह संबंध सही हो सकता है ? यदि ऐसा नहीं है तो सही संबंध का अनुमान लगाइए ।
View Solutionवायु में ध्वनि कि चाल 332 मीटर/सेकण्ड है । यदि लम्बाई का मात्रक किमी तथा समय का मात्रक घण्टा हो, तब चाल का मान क्या होगा ?
View Solutionदो वर्नियर कैलिपर्स इस तरह से हैं कि उनके मुख्य पैमाने का 1 समी, 10 समभागों में विभाजित है। एक कैलिपर (C1) के वर्नियर पमाने पर 10 बराबर भाग हैं जो कि मुख्य पैमा के 9 भागों के बराबर है। दूसरे कैलिपर (C2) के वर्नियर पैमाने पर भी 10 बराबर भाग हैं जो कि मुख्य पैमाने के 11 भागों के बराबर हैं। दोनों कैलिपर्स के पठनों को चित्र में दर्शाया गया है। C1 तथा C2 द्वारा मापे गए सही मान (सेमी में) क्रमश: हैं :
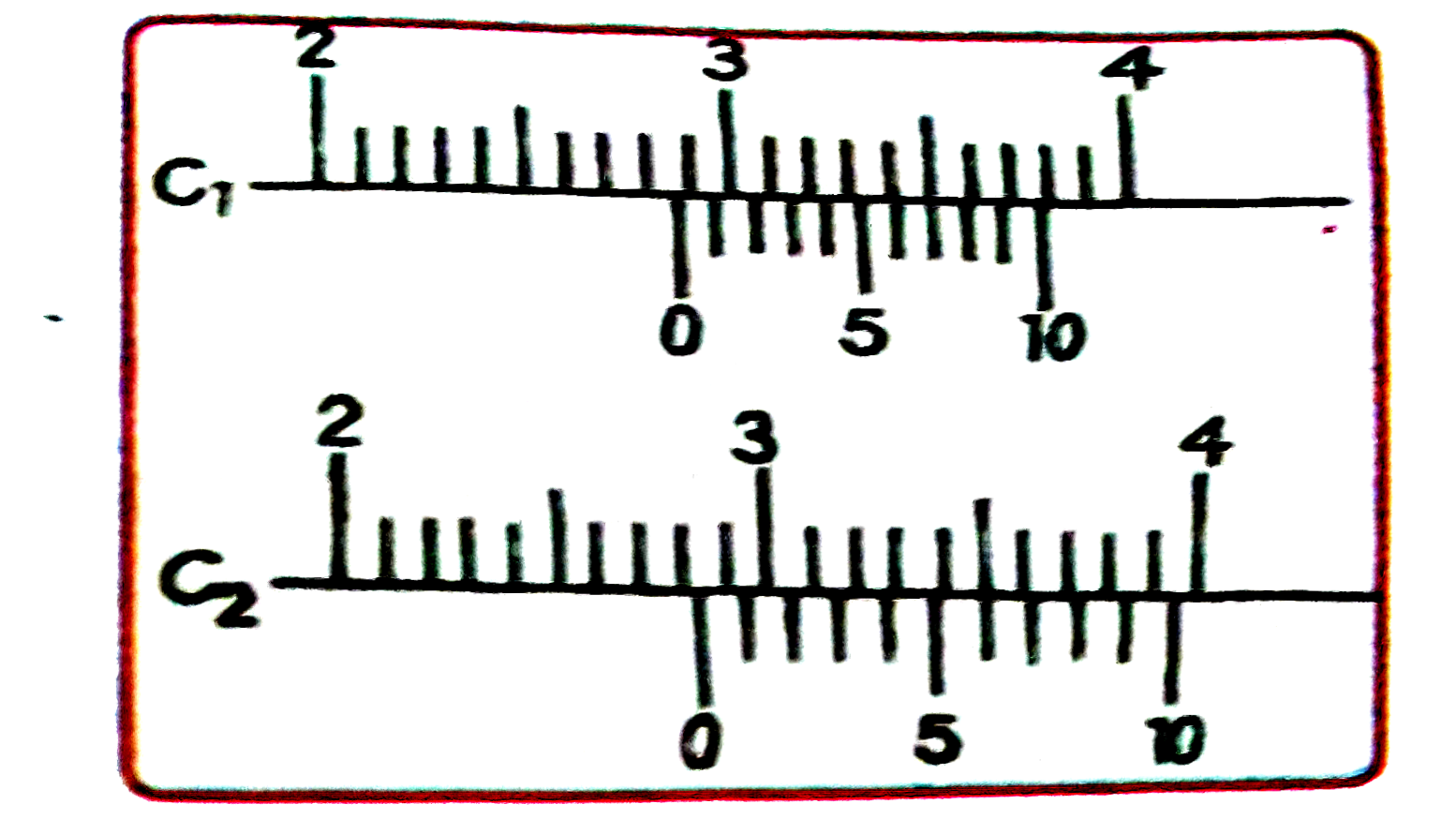
View Solutionचित्र में 0.04 kg सहती के किसी पिंड का स्थिति - समय ग्राफ दर्शाया जय है । इस गति के लिए कोई उचित भौतिक संदर्भ प्रस्तावित कीजिय। पिंड द्वारा प्राप्त दो क्रमिक आवेगों के बिच समय-अंतराल क्या है ? प्रत्येक आवेग का परिमाण क्या है ?

View SolutionIn the relaction p = (a)/(beta) e ^((aZ)/(k theta ) , p is pressure Z is distance .k is Boltamann constant and theta is the teperations . The dimensional formula of beta will be
View SolutionIn the relation P = (alpha)/(beta) e^((alpha Z)/(k theta)) , P is pressure, Z is height, k is Boltzmann constant and theta is the temperature. Find the dimensions of alpha and beta
View SolutionIn the relation, P=alpha/beta e^((alphaZ)/(ktheta))P is pressure, Z is distance, k is Boltzmann constant and theta is the temperature. The dimensional formula of beta will be-
View SolutionPressure depends on distance as, P=αβexp(−αzkθ), where α,β are constants, z is distance, k is Boltzmann's constant and θ is temperature. The dimensions of β are :
View SolutionIn the releation p=αβe−azkθ, where p is the pressure z is distance k is Boltzmann constant and θ is the temperature the dimensional formula β will be
View Solutionअल्फा बीटा, और गामा किरणोंकोक्याकहाजाताहै? अल्फा-, बीटा−औरगामा किरणों के गुणों का वर्णन करते हैं
View Solutionमाना की α,β समीकरण px2+qx+r=0,p≠0 के मूल है | यदि p,q,r समान्तर श्रेणी में हों तथा 1α+1β=4 तो | α−β | का मात्र है :
View Solutionमाना α तथा β समीकरण px2+qx+r=0,p≠0 के मूल हैं। यदि p,q, r समान्तर श्रेढ़ी में हैं तथा 1α+1β=4 है, तो |α−β | का मान है
View Solutionयदि द्विघाती समीकरण, x2+xsinθ−2sinθ=0,θ∈(0,π2), के मूल α तथा β हैं , तो α12+β12(α−12+β−12).(α−β)24 बराबर है
View SolutionPressure depends on distance as P=αβexp(−αzkθ) where αβ are constants z is distance k is Boltzmann is constant and θ is temperature. The dimension of β are
View Solution
