एक बिंदु द्रव्यमान पर दो ज्यावक्रीय ( Sinusoidal ) विस्थापन x1(t)=Asinωt एवं x2(t)=Asin(ωt+2π3) एक साथ x-दिशा में लग रहे हैं। इस द्रव्यमान पर तीसरा ज्यावक्रीय विस्थापन x3(t)=Bsin(ωt+ϕ) लगाने पर वह पूर्ण रूप से रुक जाता है। B तथा ϕ का मान है
√2A,3π4
A,4π3
√3A,5π6
A,π3
The correct Answer is:B
प्रश्नानुसार
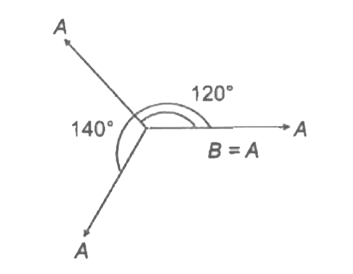
x1+x2+x3=0
Asinωt+Asin(ωt+2π3)+Bsin(ωt+ϕ)=0
यह समीकरण केवल तभी सत्य है जब
B=A तथा ϕ=4π3
अतः .B=A,ϕ=240∘=4π3
Topper's Solved these Questions
- सरल आवर्त गति BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सरल आवर्त गति EXERCISE - बहुविकल्पीय प्रश्न II (एक से अधिक विकल्प सही हैं )
6 Videos
- सरल आवर्त गति BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सरल आवर्त गति EXERCISE - रिक्त स्थानों की पूर्ति कीजिए
2 Videos
- शुद्धगतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - शुद्धगतिकी EXERCISE - विश्लेषणात्मक प्रश्न
9 Videos
- सामान्य भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सामान्य भौतिकी EXERCISE - विश्लेषणात्मक प्रश्न
9 Videos
Similar Questions
एक रैखिक सरल आवर्ती दोलित्र का बल नियतांक 2×106 न्यूटन / मी तथा आयाम 0.01 मी है, इसकी कुल यांत्रिक ऊर्जा160 जूल है। इसकी
View Solutionदो सरल आवर्त गतियाँ y1=10sin(3πt+π4) तथा y2=5[sin3πt+√3cos3πt] समीकरणों से प्रदर्शित की जाती है। इनके आयामों का अनुपात............. है, इन गतियों के आवर्तकाल.............. हैं।
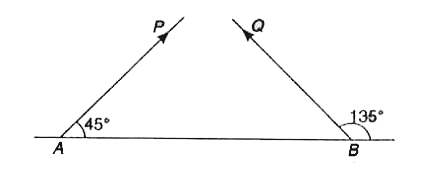
View Solutionभूमि पर स्थित दो बिंदुओं A तथा B से दो कण P तथा Q जिनके द्रव्यमान क्रमशः 20 ग्राम तथा 40 ग्राम है, प्रक्षेपित किये जाते है। P तथा Q के प्रारंभिक वेग क्षैतिज AB से चित्रानुसार क्रमशः 45∘ तथा 135∘ के कोण बनाते है। प्रत्येक कण की प्रारंभिक चाल 49 मी/से तथा दुरी AB ,245 मी है। दोनों कण समान ऊर्ध्वाधर तल में गति करते हुए संघट्ट करते है। संघट्ट के पश्चात P अपने पथ पर लोट आता है। Q की स्थिति की गणना कीजिए जहाँ वह भूमि पर लटकाता है। संघट्ट के बाद कण Q को भूमि पर पहुंचने में कितना समय लगता है? (g=9.8 मी/से 2)
View Solutionनीचे दी गई राशियों के MKS पद्धति में मात्रक बताइए।
(i) यंग प्रत्यास्थता गुणांक
(ii) चुम्बकीय प्रेरण
(iii) लेन्सों की क्षमता
View Solutionx1=3sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
Find amplitude of resultant SHM.
View SolutionThe resultant amplitude due to super position of x_(1)=sin omegat, x_(2)=5 sin (omega t +37^(@)) and x_(3)=-15 cos omega t is :
View SolutionMatch the following
Currentsr.m.s. values(1)x0sinωt(i) x(2)x0sinωtcosωt(ii) x0√2(3)x0sinωt+x0cosωt(iii) x0(2√2)
View SolutionA point mass is subjected to two simultaneous sinusoidal displacement in x−direction, x1(t)=Asinωt and x2(t)=Asin(ω+2π3). Adding a third sinusoidal displacement x3(t)=Bsin(ωt+ϕ) brings the mass to complete rest. The value of B and ϕ are
View SolutionThe equations of two SH M's are
X1=4sin(ωt+π/2).X2=3sin(ωt+π)
View SolutionThe ratio of amplitudes of following SHM is x_(1) = A sin omega t and x_(2) = A sin omega t + A cos omega t
View SolutionFind the resultant amplitude of the following simple harmonic equations :
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
View Solutionसमीकरण x1=asinωt तथा x2=a2sinωt+a2cosωt सरल आवर्त गति को प्रदर्शित करते है। दोनों आयामों का अनुपात ज्ञात कीजिए।
View Solutionतरंगों x1=asin(ωt+π/6) व x2=acosωt में कलान्तर होगा
View SolutionThree sinusoidal displacements are applied in X-direction to a point mass in such a way that total displacement is zero and the mass comes to rest. What are the values of B and ϕ if the equations are
x1(t)=Asin2ωt
x2(t)=Asin(2ωt+4π3)
x3(t)=Bsin(2ωt+ϕ)
View SolutionA particle executes two types of SHM. x_(1) = A_(1) sin omega t " and "x_(2) = A_(2) sin [omega t+(pi)/(3)] , then find the displacement at time t=0.
View Solution
