Match the following
Currentsr.m.s. values(1)x0sinωt(i) x(2)x0sinωtcosωt(ii) x0√2(3)x0sinωt+x0cosωt(iii) x0(2√2)
1. (i), 2. (ii), 3. (iii)
1. (ii), 2. (iii), 3. (i)
1. (i), 2. (iii), 3. (ii)
None of these
The correct Answer is:b
To solve the problem of matching the given currents with their respective r.m.s. values, we will analyze each equation step by step.
1. Identify the first current equation:
x=x0sin(ωt)
- The peak value (amplitude) here is x0.
- The formula for the r.m.s. value is given by:
r.m.s. value=x0√2
- Therefore, the r.m.s. value for this equation is:
x0√2
- This matches with option (ii).
2. Identify the second current equation:
x=x0sin(ωt)cos(ωt)
- To find the peak value, we can use the identity:
sin(ωt)cos(ωt)=12sin(2ωt)
- Thus, the peak value becomes:
x0⋅12=x02
- The r.m.s. value is then:
r.m.s. value=x02√2=x02√2
- This matches with option (iii).
3. Identify the third current equation:
x=x0sin(ωt)+x0cos(ωt)
- The r.m.s. value of the sum of two sinusoidal functions can be calculated using:
r.m.s. value=√(r.m.s. of sin)2+(r.m.s. of cos)2
- The r.m.s. value for both x0sin(ωt) and x0cos(ωt) is:
x0√2
- Therefore, we have:
r.m.s. value=
⎷(x0√2)2+(x0√2)2=√x202+x202=√x20=x0
- This matches with option (i).
Final Matching:
- 1 matches with (ii): x0sin(ωt) → x0√2
- 2 matches with (iii): x0sin(ωt)cos(ωt) → x02√2
- 3 matches with (i): x0sin(ωt)+x0cos(ωt) → x0
Summary of Matches:
- 1 → (ii)
- 2 → (iii)
- 3 → (i)
x=x0sin(ωt)
- The peak value (amplitude) here is x0.
- The formula for the r.m.s. value is given by:
r.m.s. value=x0√2
- Therefore, the r.m.s. value for this equation is:
x0√2
- This matches with option (ii).
x=x0sin(ωt)cos(ωt)
- To find the peak value, we can use the identity:
sin(ωt)cos(ωt)=12sin(2ωt)
- Thus, the peak value becomes:
x0⋅12=x02
- The r.m.s. value is then:
r.m.s. value=x02√2=x02√2
- This matches with option (iii).
x=x0sin(ωt)+x0cos(ωt)
- The r.m.s. value of the sum of two sinusoidal functions can be calculated using:
r.m.s. value=√(r.m.s. of sin)2+(r.m.s. of cos)2
- The r.m.s. value for both x0sin(ωt) and x0cos(ωt) is:
x0√2
- Therefore, we have:
r.m.s. value=
⎷(x0√2)2+(x0√2)2=√x202+x202=√x20=x0
- This matches with option (i).
- 1 matches with (ii): x0sin(ωt) → x0√2
- 2 matches with (iii): x0sin(ωt)cos(ωt) → x02√2
- 3 matches with (i): x0sin(ωt)+x0cos(ωt) → x0
- 1 → (ii)
- 2 → (iii)
- 3 → (i)
Topper's Solved these Questions
Similar Questions
Knowledge Check
If i1=i0sin(ωt),i2=i02sin(ωt+ϕ), then i3=
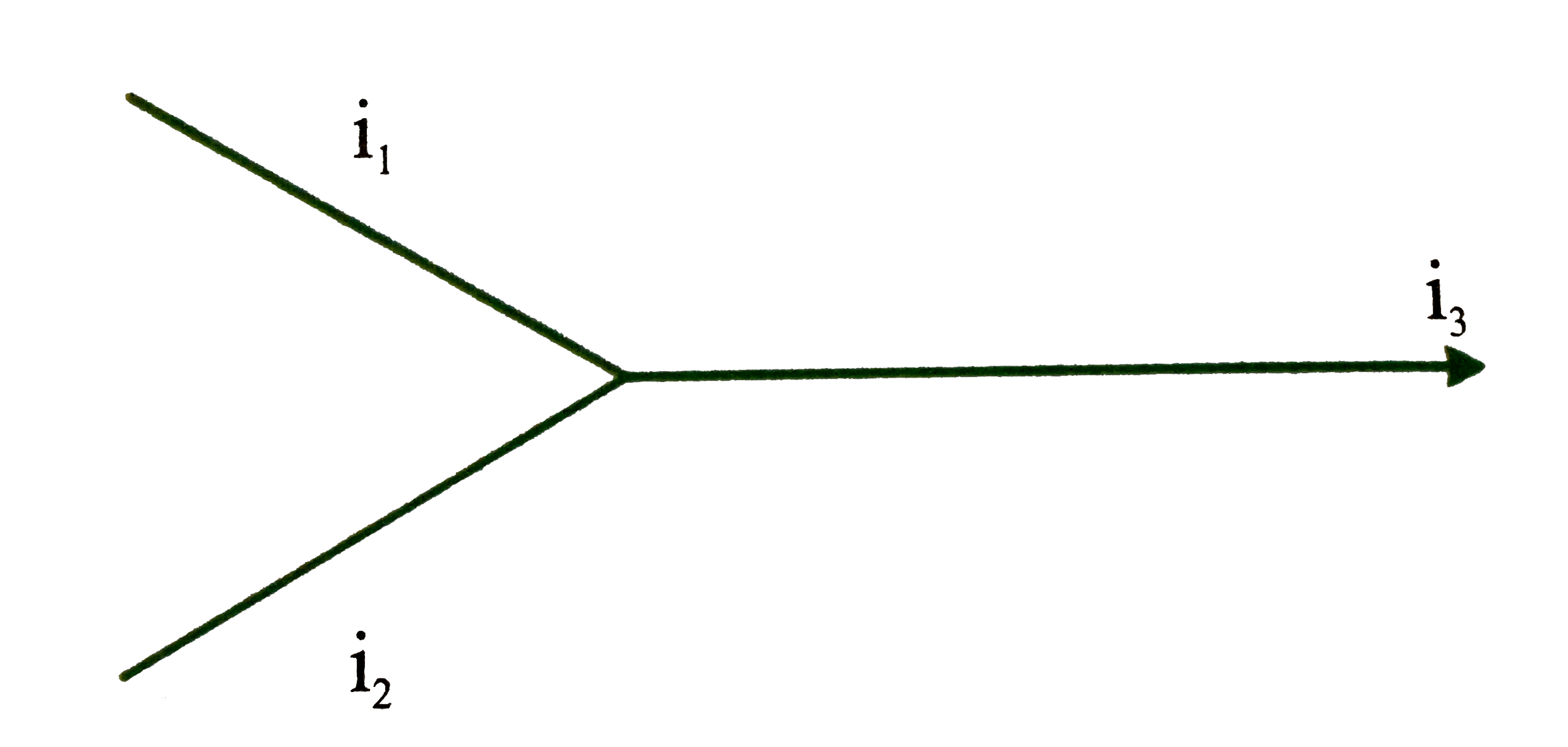 A√i201+i202sin{ϕ+ωt}B(i01+i02)sin(ϕ2+ωt)C(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]D(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ]
A√i201+i202sin{ϕ+ωt}B(i01+i02)sin(ϕ2+ωt)C(√i201+i202+2i01i02cosϕ)sin[ϕ+ωt]D(√i201+i202+2i01i02cosϕ)sin[α+ωt] where α=Tan−1[i02sinϕi01+i02cosϕ]The ratio of amplitudes of following SHM is x1=Asinωtandx2=Asinωt+Acosωt
A√2B1√2C1D2Consider two identical masses m attached to 3 identical spring as shown in the figure. They can be set in motion in two different ways as follows :
(I) x1(t)=x0cosωt and x2(t)=x0cosωt
(II) x1=(t)=x0cosωt and x2(t)=−x0cosωt
Here x1(t) and x2(t) denote the displacements from the unstreched positions. Then the potential energy stored in the system isAlarger for I than II at t = 0Blarger for I than II at t=π/ωCequal for I and II at t = 0Dsmaller for I than II at t=2π/ω
The r.m.s. value of I=I1sinωt+I2cosωt is
View SolutionIntegrate the following w.r.t.x.
xsin2x
View Solutionx1=3sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
Find amplitude of resultant SHM.
View SolutionFollowing are equations of four waves :
(i) y1=asinω(t−xv)
(ii) y2=acosω(t+xv)
(iii) z1=asinω(t−xv)
(iv) z1=acosω(t+xv)
Which of the following statements are correct ?
View SolutionWhat is the minimum phase difference between two S.H.M.s given by x2=sinωt+cosωtt and x1=12sinωt+√32cosωt
View Solution
