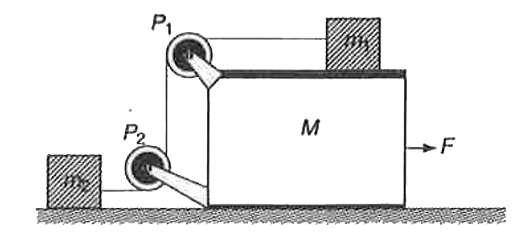
चित्र में प्रदर्शित द्रव्यमानों m1,m2 तथा M के मान क्रमशः 20 किग्रा , 5 किग्रा तथा 50 किग्रा है। M तथा भूमि के बीच घर्षण गुणांक शुन्य है। m1 तथा M के बीच और m2 तथा भूमि के बीच घर्षण गुणांक समान अर्थात 0.3 है। डोरीयों तथा घिरनियाँ भारहीन है। P1 तथा m1 के बीच और P2 तथा m2 के बीच डोरी पूर्णतया क्षैतिज स्थिति में है। P1 तथा P2 के बीच पूर्णतया उर्ध्वाधर स्थिति में है। द्रव्यमान M पर एक ब्राहा क्षैतिज बल F आरोपित किया जाता है। g का मान 10मी/से2 है।
.
(a) द्रव्यमान M के लिए सभी बलों को स्पष्टतया दर्शाता हुआ बल निर्देशक आरेख बनाइये।
(b) m1 तथा M के बीच घर्षण बल के परिमाण को f1 तथा m2 और भूमि के बीच घर्षण बल के परिमाण को f2 मानते हुए किसी विशेष बल F के लिए f1=2f2 है। f1 तथा f2 के मान क्या है ? सभी द्रव्यमानों के लिए गति की समीकरणे लीखिए। F का मान , डोरीयों में तनाव तथा द्रव्यामाओं के लिए त्वरण का मान ज्ञात कीजिए।
The correct Answer is:(b) f1=30 न्यूटन , f2=15 न्यूटन , F=60 न्यूटन T=18, न्यूटन मी/से2.
m1=20 किग्रा
m2=5 किग्रा
M=50 किग्रा
μ=0.3
तथा g=10मी/से2
.
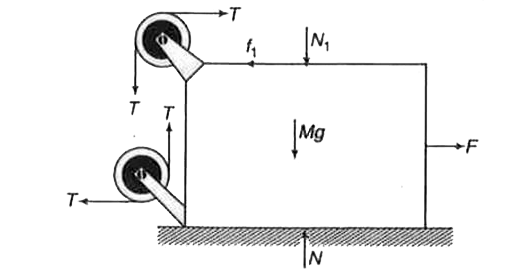
(a) द्रव्यमान M के लिए बल निर्देशक आरेख ऊपर चित्र में प्रदर्शित है।
(b)f1 का अधिकतम मान (f1)अधिकतम=(0.3)(20)(10)=60 न्यूटन f2 का अधिकतम मान (f2)अधिकतम=(0.3)(5)(10)=15 न्यूटन br> m1 व m2 पर कार्य करने वाले क्षैतिज बल ( चित्रानुसार) है।
.
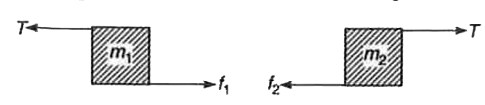यहाँ पर निम्नलिखित दो परिस्थियों संभव है।
(i) m1 व m2 भूमि के सापेक्ष स्थिर रहेंगे या
(ii) m1 या m2 भूमि के सापेक्ष गतिमान रहेंगे।
पहली स्थिति संभव है जबकि
T≤(f1)अधिकतम या T≤60 न्यूटन
तथा T≤(f2)अधिकतम
या T≤15 न्यूटन
ये स्थितियाँ केवल तभी सन्तुष्ट होंगी जब T≤14 न्यूटन
माना T=14 न्यूटन पर।
तब f1=f2=14 न्यूटन इस प्रकार स्थिति f1=2f2 सन्तुष्ट नहीं होगी तथा m1 और m2 दोनों स्थिर नहीं रह सकते है।
दूसरी स्थिति संभव है जबकि
f2=(f2)अधिकतम=15 न्यूटन
∴f1=2f2=30 न्यूटन
परन्तु चूँकि f1<(f2)अधिकतम, इसलिए m1 तथा M के बीच कोई आपेक्षिक गति संभव नहीं है अर्थात सभी द्रव्यमान समान त्वरण से गतिमान होंगे। माना यह समान त्वरण a है।
∴f2=15 न्यूटन तथा f1=30 न्यूटन
बल निर्देशक आरेख तथा गति के समीकरण निम्न प्रकार है :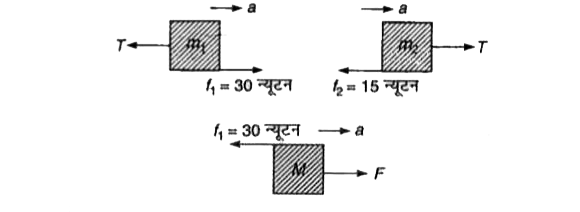 
.
m1 के लिए 300T=20a ....(i)
m2 के लिए T−15=5a ......(ii)
M के लिए F−30=50a.....(iii)
हल करने पर F=60 न्यूटन T=18 न्यूटन a=35मी/से2.
Topper's Solved these Questions
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गति के नियम EXERCISE - श्रृंखलाबद्ध -बोधन प्रकार2videos
गति के नियम
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गति के नियम EXERCISE - एकल पूर्णांक उत्तर प्रकार2videos
गति के नियम
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - कार्य ऊर्जा एव सामर्थ्य EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार6videos
कार्य ऊर्जा एव सामर्थ्य
- BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गुरुत्वाकर्षण EXERCISE - विश्लेषणात्मक प्रश्न5videos
गुरुत्वाकर्षण
Similar Questions
एक रुक्ष पृथ के उच्चतम बिन्दु से 1 किग्रा द्रव्यमान के गुटके को विरामावस्था से छोडा जाता है। यह पथ 40 मी त्रिज्या का वृत्तीय चाप है। गुटका अपने पथ पर बिना लड़के हुए सरकता है। इस गुटके पर एक घर्षण बल तात्क्षणिक वेग की विपरीत दिशा में लगता है। चित्र में दर्शाए गए अनुसार , बिन्दु O तक आने के लिए घर्षण को अतिक्रम करने के लिए 150 जूल कार्य करना पड़ा है। (गुरुत्वीय त्वरण g=10मी/से2 लीजिए)
.
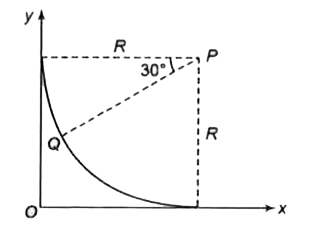जब गुटका बिन्दु Q पर पहुँचता है , इसकी गति है03:52View Solutionद्रव्यमान 0.36 किग्रा तथा 0.72 किग्रा के दो पिण्ड , एक हलकी व न खिंचने वाली डोरी के सिरों से बंधे है। यह डोरी , चित्र में दिखाए गए ढंग से , एक स्थिर तथा चिकनी घिरनी के ऊपर से जाती है। अब पिण्डों को विराम अवस्था से छोड़ दिया जाता है। रस्सी में तनाव बल द्वारा 0.36 किग्रा द्रव्यमान वाला पिण्ड पर पहले सेकंड में किए गए कार्य का मान जल में निकाले। अपनी गणना g=10मी/से2 लेकर करें।
03:14View Solutionएक नत समतल के घर्षण रहित पृष्ठ पर M द्रव्यमान का एक छोटा गुटका गतिमान है, बिंदु B पर नत समतल का कोण 60∘से 30∘ अचानक परिवर्तित होता है। गुटका प्रारम्भ में बिंदु A पर विरामावस्था में है। नत समतल तथा गुटके के बिच संघट्ट अप्रत्यास्थ माना गया (g=10मीसे2)
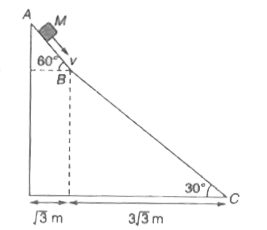
दूसरे नत समतल से टकराने के तुरंत बाद बिंदु B पर गुटके की चाल है05:42View Solutionदो उपग्रह S1 व S2 एक ग्रह के चारों ओर समतलीय वृत्ताकार कक्षाओं में एक ही दिशा में घूमते हैं। उनके परिक्रमण काल क्रमश: 1 घण्टा व 8 घण्टा हैं। S1 की कक्षा की त्रिज्या 104 किमी है। जब S2,S1 के निकटस्थ है तो ज्ञात कीजिए (a) S1 के सापेक्ष S2 की चाल, (b) S1 में बैठे अन्तरिक्ष यात्री द्वारा वास्तविक रूप से प्रेक्षित S2 की कोणीय चाल।
07:15View Solutionयदि मूलबिंदु O के सापेक्ष त्रिभुज ABC के शीर्षों के स्थिति सदिश क्रमशः (1,−1,2),(2,1,3) और (−1,2,−1) है| तथा इसके केन्द्रक का स्थिति सदिश ज्ञात कीजिए|
01:28View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
02:41View Solutionरेखा तथा वृत्त के स्पर्श बिंदु के निर्देशांक ……………. है ।
04:24View Solutionवक्रों x+2y2=0 तथा x+3y2=1 के बीच घिरे क्षेत्र का क्षेत्रफल है :
05:19View Solutionबिंदुओं (1, 4, 5) तथा (2, 2, 3) के बीच की दुरी कितनी होगी ?
08:14View Solutionरेखा x−2a=y−2b=z−2c तथा समतल ax+by+cz+6=0 के बीच का कोण है -
04:25View Solutionबिंदु (32,0) तथा वक्र y=√x,(x>0) के बीच की न्यूतनम दुरी है
03:35View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
05:21View Solutionमाना √3ˆi+ˆj,ˆi+√3ˆj तथा βˆi+(1−β)ˆj क्रमश: तीन बिन्दुओ A,B तथा C के मूलबिंदु O के सापेक्ष, स्थिति सदिश है । यदि C की, OA तथा OB के बीच बने न्यूनकोण के समद्विभाजक से दुरी 3√2 है, तो β के सभी संभावित मानो का योग है
02:27View Solutionएक शतरंज प्रतियोगिता में m पुरुष तथा दो महिलाएं भाग ले रही है । प्रत्येक प्रतिभागी (participant) दूसरे प्रत्येक प्रतिभागी के साथ दो गेम खेलता है । यदि पुरुषो के बीच आपस में खेले गए गेमों कि संख्या, पुरुष तथा महिलाओ के बीच खेले गए गेमों की संख्या से 84 अधिक है , तो m का मान है
01:03:39View Solutionवक्र y=ex,y=e−x तथा सरल रेखा x=1 के बीच घिरे क्षेत्र का क्षेत्रफल है।
03:10View Solutionसूर्य और पृथ्वी के बीच की दूरी 1.496×108 km है तथा पृथ्वी और चंद्रमा के बीच की दूरी 3.84×108m है सूर्य ग्रहण होने पर चन्द्रमा पृथ्वी और सूर्य के बीच में आ जाता है इस विशेष समय पर सूर्य और चंद्रमा के बीच की दूरी क्या है ?
02:02View Solution