तीन द्रव्यमान M1,M2 तथा M3 एक नगण्य द्रव्यमान वाली डोरी द्वारा जुड़े जो कि नगण्य द्रव्यमान वाले घर्षण रहित घिरनियाँ P1 व P2 से चित्रानुसार गुजरती है। द्रव्यमान इस प्रकार गति कहते है कि P1 व P2 के बीच डोरी का भाग नत समतल के समान्तर रहता है तथा P2 व P3 के बीच का भाग क्षैतिज रहता है । M2 तथा M3 में से प्रत्येक का द्रव्यमान 4.0 किग्रा तथा द्रव्यमानों व तालों के बीच का गतिज घर्षण गुणांक 0.25 है। नत समतल क्षैतिज से 37∘ का कोण बनता है। यदि M1 नीचे की और समान वेग से गतिमान हो तो ज्ञात कीजिए :
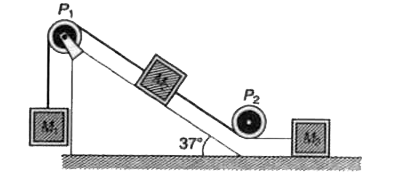 .
.
(g=9.8मी/से2,sin37∘=3/5).
(a) द्रव्यमान M1
(b) डोरी के क्षैतिज भाग में तनाव
9.8 किग्रा , 9.8 न्यूटन
4.2 किग्रा , 9.8 न्यूटन
1.2 किग्रा , 4.9 न्यूटन
4.2 किग्रा , 4.9 न्यूटन
The correct Answer is:B
नियत वेग का अर्थ है कि नेट त्वरण का मान शून्य है ( नेट खिंचाव बल जो निकाय पर कार्य कर रहा है वह शून्य है) नेट खिंचाव बल की गणना में तनाव बलों को नहीं लिया गया है। इस प्रकार
(a) M1g=M2gsin37∘+μM2gcos37∘+μM3g
या M1=M2sin37∘+μM2cos37∘+μM3
मान प्रतिस्थापित करने पर
M1=(4)(35)+(0.25)(4)(45)+(0.25)(4)
=4.2 किग्रा
(b) चूँकि M3 एकसमान वेग से गतिमान है
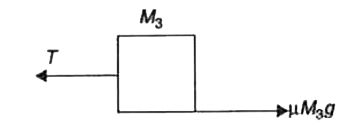
अतः T=μM3g=(0.25)(4)(9.8)
=9.8 न्यूटन
Topper's Solved these Questions
- गति के नियम BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गति के नियम EXERCISE - श्रृंखलाबद्ध -बोधन प्रकार
2 Videos
- गति के नियम BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गति के नियम EXERCISE - एकल पूर्णांक उत्तर प्रकार
2 Videos
- कार्य ऊर्जा एव सामर्थ्य BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - कार्य ऊर्जा एव सामर्थ्य EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
6 Videos
- गुरुत्वाकर्षण BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गुरुत्वाकर्षण EXERCISE - विश्लेषणात्मक प्रश्न
5 Videos
Similar Questions
एक रुक्ष पृथ के उच्चतम बिन्दु से 1 किग्रा द्रव्यमान के गुटके को विरामावस्था से छोडा जाता है। यह पथ 40 मी त्रिज्या का वृत्तीय चाप है। गुटका अपने पथ पर बिना लड़के हुए सरकता है। इस गुटके पर एक घर्षण बल तात्क्षणिक वेग की विपरीत दिशा में लगता है। चित्र में दर्शाए गए अनुसार , बिन्दु O तक आने के लिए घर्षण को अतिक्रम करने के लिए 150 जूल कार्य करना पड़ा है। (गुरुत्वीय त्वरण g=10मी/से2 लीजिए)
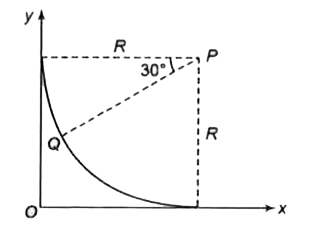 .
.
जब गुटका बिन्दु Q पर पहुँचता है , इसकी गति है
View Solutionद्रव्यमान 0.36 किग्रा तथा 0.72 किग्रा के दो पिण्ड , एक हलकी व न खिंचने वाली डोरी के सिरों से बंधे है। यह डोरी , चित्र में दिखाए गए ढंग से , एक स्थिर तथा चिकनी घिरनी के ऊपर से जाती है। अब पिण्डों को विराम अवस्था से छोड़ दिया जाता है। रस्सी में तनाव बल द्वारा 0.36 किग्रा द्रव्यमान वाला पिण्ड पर पहले सेकंड में किए गए कार्य का मान जल में निकाले। अपनी गणना g=10मी/से2 लेकर करें।
View Solutionएक नत समतल के घर्षण रहित पृष्ठ पर M द्रव्यमान का एक छोटा गुटका गतिमान है, बिंदु B पर नत समतल का कोण 60∘से 30∘ अचानक परिवर्तित होता है। गुटका प्रारम्भ में बिंदु A पर विरामावस्था में है। नत समतल तथा गुटके के बिच संघट्ट अप्रत्यास्थ माना गया (g=10मीसे2)
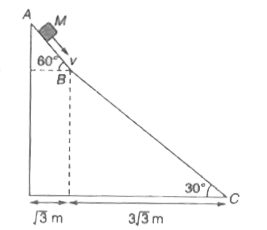
दूसरे नत समतल से टकराने के तुरंत बाद बिंदु B पर गुटके की चाल है
View Solutionदो उपग्रह S1 व S2 एक ग्रह के चारों ओर समतलीय वृत्ताकार कक्षाओं में एक ही दिशा में घूमते हैं। उनके परिक्रमण काल क्रमश: 1 घण्टा व 8 घण्टा हैं। S1 की कक्षा की त्रिज्या 104 किमी है। जब S2,S1 के निकटस्थ है तो ज्ञात कीजिए (a) S1 के सापेक्ष S2 की चाल, (b) S1 में बैठे अन्तरिक्ष यात्री द्वारा वास्तविक रूप से प्रेक्षित S2 की कोणीय चाल।
View Solutionएक इलेक्ट्रॉन (द्रव्यमान किग्रा) व एक प्रोटॉन (द्रव्यमान किग्रा) के बीच गुरुत्वाकर्षण-बल व स्थिरवैघुत बल का अनुपात ज्ञात कीजिए। (e=1.6×10−19 कूलाम तथा G=6.67×10−11 (न्यूटन-मीटर^(2)/किग्रा^(2))
View Solutionदो वस्तुओ की गतिज ऊर्जाओ समान है। यदि इनके द्रव्यमान m1 व m2 तथा संवेग क्रमश: p1 व p2 हो तो अनुपात p1/p2 कितना होगा?
View Solutionएक कम्पनी दो प्रकार के टेलीफोनों का निर्माण करती है|पहला डोरी युक्त,दूसरा डोरी रहित| डोरी युक्त टेलीफ़ोन के निर्माण में 2 घंटे लगते है तथा रहित डोरी मॉडल के निर्माण में 4 घंटे लगते है| कम्पनी के पास इन प्रतिरूपों के निर्माण के लिए प्रतिदिन अधिक से अधिक 800 कार्य घंटे उपलब्ध है तथा पैकिंग विभाग प्रतिदिन अधिक से अधिक 300 टेलीफ़ोन सेटों को पैक कर सकता है|यदि कम्पनी डोरी युक्त मॉडल को रु 300 में बेचती है तथा डोरी रहित मॉडल को रु 400 में बचती है ,तो उसे प्रत्येक प्रकार के कितने टेलीफ़ोन सेल प्रतिदिन निर्मित करने चाहिए जिससे की उसकी बिक्री अधिकतम हो?
View Solutionगुरुत्व त्वरण G के मान का परिकलन | द्रव्यमान तथा भार
View Solutionयदि m1 व m2 अतिपरवलय x225−y216=1 की स्पर्श रेखाओं की प्रवणताएं हो, जो बिन्दु (6,2) से गुजरती है , तो
View Solutionद्रव्यमान केंद्र की गति व कणो के निकाय का रेखीय संवेग
View Solutionविभिन्न वस्तुओं का द्रव्यमान केंद्र।द्रव्यमान केंद्र की गति व कणो के निकाय का रेखीय संवेग
View Solutionm1 व m2 द्रव्यमानों के दो कणों के किसी निकाय का द्रव्यमान केन्द्र, m1 से d1 दूरी पर तथा m2 से d2 दूरी पर इस प्रकार से है कि
View Solutionआण्विक तथा मोलर द्रव्यमान कैसे निकालते है
View SolutionTwo bodies of different masses m1 and m2 have equal momenta. Their kinetic energies E1 and E2 are in the ratio
View SolutionMatch the column - The mass m_(1), m_(2) And M is arranged as shown. All surfaces are frictionless and the chord is incongruous. A fixed force F, m_(1) The mass is applied to the J block. The pulleys and the cord are light. The part of the lanyard between the two pulleys is vertical, and the pulleys have a mass m_(1) and m_(2) The chord portion connecting to is horizontal. {:("(P) द्रव्यमान " m_(1) " का त्वरण " ,"(1) " (F)/(m_(1))),("(Q) द्रव्यमान" m_(2) " का त्वरण ","(2) " (F)/(m_(1)+m_(2))),("(R) द्रव्यमान M का त्वरण ","(3) शून्य "),("(S) डोरी में तनाव ","(4) "(m_(2)F)/(m_(1)+m_(2))):}
View SolutionIf m1andm2 satisfy the relation
m+5Pm+1=112(m-1)(m+3Pm)
then m1+m2 is equal to
View Solution
