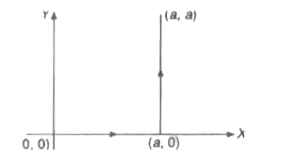
xy -ताल में गतिमान एक कण पर बल F=−k(yˆi+xˆj) (जहाँ k एक धनात्मक नियंतर है) कार्य करता है। मूल बिंदु से प्रप्राम्भ करते हुए पहले कण को धन X -अक्ष की दिशा में बिंदु (a,0) तक ले जाता है, पुनः Y -अक्ष के समान्तर बिंदु (a ,a ) तक ले जाया जाता है। कण पर बल F द्वारा किया गया कार्य है
−2ka2
2ka2
−ka2
ka2
The correct Answer is:C
dW=F.ds जहां ds=dxˆi+dyˆj+dzˆk
तथा F=−k(yˆi+xˆj)
∴dW=−k(ydx+xdy)=−kd(xy)
⇒W=∫a,a0,0dW=−k∫a,a0,0d(xy)=−k[xy]a,a0,0
या W=−ka2
Topper's Solved these Questions
- कार्य ऊर्जा एव सामर्थ्य BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - कार्य ऊर्जा एव सामर्थ्य EXERCISE - बहुविकल्पीय प्रश्न II (एक से अधिक विकल्प सही है)
1 Video
- कार्य ऊर्जा एव सामर्थ्य BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - कार्य ऊर्जा एव सामर्थ्य EXERCISE - दृढ़कथन-कारण प्रकार
1 Video
- ऊष्मा एवं उष्मागतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - ऊष्मा एवं उष्मागतिकी EXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
- गति के नियम BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गति के नियम EXERCISE - श्रृंखलाबद्ध -बोधन प्रकार
2 Videos
Similar Questions
एक कण नियत परिमाण का एक बल इस प्रकार कार्य करता है की उसकी दिशा कण के वेग की दिशा के सदैव लंबवत रहती है। कण की गति एक निश्चित ताल में होती है, इससे पता चलता है कि
View Solutionकथन-I m द्रव्यमान का एक ब्लॉक एक रुक्ष क्षैतिज तल पर v वेग से चलना प्रारम्भ करता है। ब्लॉक तथा तल के बीच के घर्षण के कारण यह कुछ दूर चलकर रुक जातः है । जब इस क्षैतिज ताल को क्षैतिज से 30∘ के कोण पर झुका दिया जाता है तथा उसी ब्लॉक को ताल पर ऊपर कि और प्रारंभिक वेग v से चला दिया जाता है। इस दूसरी स्थिति में होने वाली यांत्रिक ऊर्जा का हास्य पहली स्थिति में होने वाली ऊर्जा के हास्य से कम है।
कथन-II ब्लॉक तथा ताल के बीच का घर्षण गुणांक झुकाव कोण के बढ़ने से घटता है।
View Solutionऊष्मा के चालक पदार्थ से बने तथा स्थिर रखे गए बेलन की त्रिज्या R तथा ऊँचाई L0 है | बेलन नीचे से खुला है तथा इसके ऊपरी सिरे में एक छोटा छेद है, जैसा कि चित्र में दिखाया गया है | एक पिस्टन जिसका द्रव्यमान M है, ऊपरी सतह से L दुरी पर पकड़ा हुआ है | वायुमण्डलीय दाब P0 है |
अब पिस्टन को बाहर की ओर धीरे - धीरे खिंचा जाता है तथा ऊपर से 2L दूरी पर पकड़ कर रखा जाता है, तब बेलन में ऊपरी सिरे तथा पिस्टन के बीच के भाग में दाब होगा |

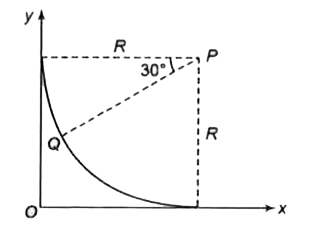
View Solutionएक रुक्ष पृथ के उच्चतम बिन्दु से 1 किग्रा द्रव्यमान के गुटके को विरामावस्था से छोडा जाता है। यह पथ 40 मी त्रिज्या का वृत्तीय चाप है। गुटका अपने पथ पर बिना लड़के हुए सरकता है। इस गुटके पर एक घर्षण बल तात्क्षणिक वेग की विपरीत दिशा में लगता है। चित्र में दर्शाए गए अनुसार , बिन्दु O तक आने के लिए घर्षण को अतिक्रम करने के लिए 150 जूल कार्य करना पड़ा है। (गुरुत्वीय त्वरण g=10मी/से2 लीजिए)
 .
.
जब गुटका बिन्दु Q पर पहुँचता है , इसकी गति है
View Solutionद्रव्यमान m के एक कण को गति y=ut+12gt2 से वर्णित है । उस कण पर लगने वाले बल को ज्ञात करो ।
View Solutionनिर्देशाक्षो को प्रारंभिक निर्देशांकों के समांतर रखते हुए मूल बिंदु को बिंदु P पर हटाने पर समीकरण ax+by+c=0 समीकरण ax+by+c+λ=0 के रूप में बदल जाता है सिद्ध कीजिए कि P बिन्दुपथ ax+by=λ होगा ।
View Solutionएक रेखा X- अक्ष तथा Y-अक्ष को बिंदु A तथा B पर मिलती है AB का मध्य बिंदु (x1,y1) है तो रेखा का समीकरण है -
View Solutionबल F=(ˆi+ˆj+ˆk) के द्वारा कण पर कृत कार्य की गणना कीजिए यदि वह बल कण को बिंदु A(3, 3, 3) से बिन्दु (4, 4, 4) पर स्थानान्तरित कर देता है।
View Solutionएक कण पर दो अचर बल (2ˆi+5ˆj+6ˆk) तथा (−ˆi−2ˆj−ˆk) क्रिया करते हैं। इन बलों के कारण कण बिन्दु (4ˆi−3ˆj−2ˆk) से बिन्दु (6ˆi+ˆj−3ˆk) पर स्थानान्तरित हो जाता है। बल द्वारा कृत कार्य की गणना कीजिए।
View Solutionबिंदु (18, 5, 12) की X-अक्ष से पर लंबवत्त दुरी........ है |
View Solutionनिम्नलिखित स्थितियों में एक चर बिंदु का बिन्दुपथ ज्ञात कीजिए जिसकी
x-अक्ष और y-अक्ष से दूरी सदैव बराबर रहती है ।
View Solutionउस बिंदु का बिन्दुपथ ज्ञात कीजिए
जिसकी x-अक्ष से दूरी उसकी y-अक्ष से दूरी की तीन गुनी है ।
View Solutionएक कण y=x2+2x से साथ-साथ चलता है। व्रक के किस बिंदु पर x तथा y निर्देशांक समान दर से परिवर्तित हो रहे है ?
View Solutionवह समतल, जो बिन्दुओ (−3,−3,4) तथा (3,7,6) को मिलाने वाले रेखाखण्ड का लंबसमद्विभाजक करता है, निम्न में से किस एक बिंदु से होकर जाता है?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solution