एक नत समतल के घर्षण रहित पृष्ठ पर M द्रव्यमान का एक छोटा गुटका गतिमान है, बिंदु B पर नत समतल का कोण 60∘से 30∘ अचानक परिवर्तित होता है। गुटका प्रारम्भ में बिंदु A पर विरामावस्था में है। नत समतल तथा गुटके के बिच संघट्ट अप्रत्यास्थ माना गया (g=10मीसे2)

यदि गुयतके तथा नत समतल के बिच संघट्ट पूर्णता प्रत्यास्थ हो, तब बिंदु B पर गुटके के वेग का ऊर्ध्वर (ऊपर की और) घातक (दूसरे नत समतल से टकराने के तुरंत बाद ) है
√30 मी/से
√15मी/से
शून्य
−√15 मी/से
प्रत्यास्था टक्कर में v का BC के समांतर घतक अपरिवर्तित रहेगा जबकि BC के लंबवत घतक परिमाण में अपहरिवर्तित रहेगा परन्तु इसकी दिशा विपरीत हो जाएगी।
Topper's Solved these Questions
- कार्य ऊर्जा एव सामर्थ्य BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - कार्य ऊर्जा एव सामर्थ्य EXERCISE - विश्लेषणात्मक प्रश्न
9 Videos
- ऊष्मा एवं उष्मागतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - ऊष्मा एवं उष्मागतिकी EXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
- गति के नियम BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गति के नियम EXERCISE - श्रृंखलाबद्ध -बोधन प्रकार
2 Videos
Similar Questions
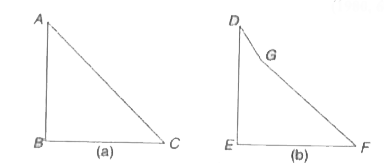
a तथा b में AC ,DG तथा GF सिथत नत समतल है, BC=EF=x तथा AB=DE=y है। M द्रव्यमान का एक छोटे ब्लॉक बिंदु A से छोड़ा जाता है यह AC के अनुदिश फिसलते हुए vC चाल से बिंदु C पर पहुँचता है। समान द्रव्यमान बिंदु D से छोड़ा जाता है, DGF के अनुदिश फिसलते हुए यह द्रव्यमान बिंदु F पर vF चाल से पहुँचता है। यदि ब्लॉक तथा टालो AC व DGF के बिच गतिज घर्षण गुणक μ हो तो vC तथा vF के मान क्या होंगे ?
View Solutionऊष्मा के चालक पदार्थ से बने तथा स्थिर रखे गए बेलन की त्रिज्या R तथा ऊँचाई L0 है | बेलन नीचे से खुला है तथा इसके ऊपरी सिरे में एक छोटा छेद है, जैसा कि चित्र में दिखाया गया है | एक पिस्टन जिसका द्रव्यमान M है, ऊपरी सतह से L दुरी पर पकड़ा हुआ है | वायुमण्डलीय दाब P0 है |
अब पिस्टन को बाहर की ओर धीरे - धीरे खिंचा जाता है तथा ऊपर से 2L दूरी पर पकड़ कर रखा जाता है, तब बेलन में ऊपरी सिरे तथा पिस्टन के बीच के भाग में दाब होगा |

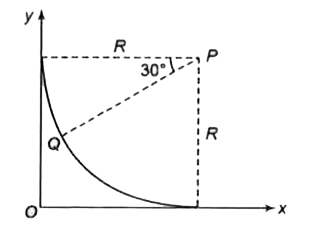
View Solutionएक रुक्ष पृथ के उच्चतम बिन्दु से 1 किग्रा द्रव्यमान के गुटके को विरामावस्था से छोडा जाता है। यह पथ 40 मी त्रिज्या का वृत्तीय चाप है। गुटका अपने पथ पर बिना लड़के हुए सरकता है। इस गुटके पर एक घर्षण बल तात्क्षणिक वेग की विपरीत दिशा में लगता है। चित्र में दर्शाए गए अनुसार , बिन्दु O तक आने के लिए घर्षण को अतिक्रम करने के लिए 150 जूल कार्य करना पड़ा है। (गुरुत्वीय त्वरण g=10मी/से2 लीजिए)
 .
.
जब गुटका बिन्दु Q पर पहुँचता है , इसकी गति है
View Solutionबिन्दुओ (4,-1,2) और (-3,2,3) को मिलाने वाली रेखा एक समतल को बिंदु (-10,5,4) पर लंबवत मिलती है समतल का समीकरण ज्ञात कीजिये
View Solutionसमतल में लुढ़कने वले वृत्त के केंद्र का बिंदु पथ होता है:
View Solutionउस समतल का सदिश समीकरण जो बिन्दु A(4,7,−4) से जाता है तथा सदिश (3,2,−1)पर लम्ब है -
View Solutionवह समतल, जो बिन्दुओ (−3,−3,4) तथा (3,7,6) को मिलाने वाले रेखाखण्ड का लंबसमद्विभाजक करता है, निम्न में से किस एक बिंदु से होकर जाता है?
View Solutionरेखा x−42=y−52=z−31 तथा समतल x+y+z=2 का प्रतिच्छेदन बिंदु निम्न में से किस रेखा पर स्थित है ?
View Solutionयदि बिन्दु (2,α,β) उस समतल पर स्थित है, जो बिन्दुओ (3,4,2) तथा (7,0,6) से होकर जाता है तथा समतल 2x−5y=15 के लंबवत है, तो 2α−3β बराबर है
View Solutionबिंदु (3,4,5) से समतल x+y+z=9 पर डाले गए लम्ब का पाद बिंदु होगा
View Solutionएक समतल निर्देशाक्षों को क्रमश: A, B तथा C पर काटता है। यदि △ABC का केन्द्रक (2,-1, 3) है, तो समतल का समीकरण ज्ञात कीजिए।
View Solutionसमतल|अभिलम्ब रूप में समतल का समीकरण#!#एक दिए गए सदिश के अनुलम्ब एवं दिए गए बिंदु से होकर जाने वाले समतल का समीकरण#!#तीन असंरेखीय बिंदुओं से होकर जाने वाले समतल का समीकरण#!#समतल का अंत:खंड रूप#!#उदाहरण
View Solutionदो समतलीय का सह-तलीय होना|दो समतलों के बीच कोण#!#समतल से दिए गए बिंदु की दूरी#!#एक रेखा एवं एक समतल के बीच कोण#!#उदाहरण
View Solutionघर्षण रहित नत तल पर रखे गुटके की गति
View Solutionघर्षण रहित नत तल पर रखे गुटकों की गति
View Solutionनत समतल पर प्रक्षेप्य गति
View Solution
